精心设计 精准定位
——以“正切函数的图象与性质”的教学为例
王德军
(南京师范大学第二附属中学,211900)
教学设计的精准定位是衡量一节课优劣的重要指标.围绕教材,基于学情,瞄准核心素养展开设计,有助于实现教学目标,打造高效课堂,提升学生数学学习的能力.本文结合“正切函数的图象与性质”一节课的两种教学设计及实施过程谈谈一些想法.
一、教学实录一
1.引入
师:前面我们学习了正、余弦函数的图象与性质,今天我们进一步学习正切函数的图象与性质.结合已学知识,对于正切函数我们知道了什么?
师:还有其他我们已知的吗?
生:周期和奇偶性.
师:如何得到上述结论?
生:由诱导公式 tan(-x)=-tanx及tan(π+x)=tanx.
2.探究
问题1如何作正切函数的图象?(学生思考并相互讨论,给定足够时间)
生:用“五点法”作图来完成.
师:五点作图是在完全作出完整图象的情况下总结出来的近似画法,面对一个新函数,显然“五点法”是不适合的.
生:利用描点.
师:我们可以将作图的作法总结如下,一般作图可分为代数描点和几何描点,前者粗略,后者作图较为准确.
追问1:确定了作法,请类比正弦函数图象作法,将分几步完成.
生:第一步:先作一个周期内图象;第二步:再将一个周期内图象向左向右平移拓展到整个定义域中.
追问2:先作哪个区间内的图象?
生:[0,π].
师:还有其他方案吗?

追问3:哪种方案最佳?
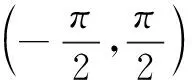
3.结论
通过几何画板作出正切函数图象,请同学们结合正切函数图象探讨未知的性质.
师:有无不同意见?(思考片刻,没有任何反应,老师引导,学生观察在定义域中被挖去的点与图象之间存在什么关系?)
师:好的,通过图象我们将正切函数的基本性质已经归纳出来了.
问题2函数y=tanx在定义域上是单调函数吗?
生:当x1=0,x2=π时,由于x1 4.应用 (由学生讲思考过程,老师板书) 设计意图引导学生利用化归思想将有关正切函数的复杂形式通过整体法转化为正切函数,利用其性质解决问题. 例2比较大小 (1)tan 167°,tan 173° ; 设计意图正切值的大小比较.我们一般首选函数的单调性来完成,遇见复杂的角,我们通常利用正切函数的周期来化简,并将其统一到一个单调区间,完成大小比较. 5.小结 本节课你有何收获? 知识层面:(1)正切函数图象的画法;(2)正切函数的性质;(3)正切函数性质的简单应用. 基本活动经验:类比、数形结合思想的渗透. 1.回顾复习,引入新课 所有同学一起口答填表,复习正、余弦函数的性质:图象、定义域、值域、最值、单调性、奇偶性、周期及对称性. 生:由图象归纳而来. 讨论1:研究正、余弦函数图象的方法是什么? 学生讨论后得出方法有画单位圆,五点作图法,平移正弦线等. 师:结合大家的想法,我们一起回顾正弦函数的图象的作法. (1) 确定一个周期,分成若干等分; (2) 利用单位圆,平移正弦线; (3) 用光滑的曲线将正弦线的端点顺次连接. 讨论2:我们今天研究正切函数的图象与性质,如何来作正切函数图象? 通过研讨,很快有部分学生给出答案:类比正、余弦函数的图象作法. 2.学生探究,解决问题 问题1y=tanx的最小正周期是不是2π? 生:周期是π,因为tan(π+x)=tanx. 师:你会论证吗?(思考片刻无人作出反应,由老师引导给出证明) =tanx, ∴正切函数y=tanx的最小正周期是π. 问题2研究哪个周期上的图象比较好呢? 同学们拿出纸,先独立画函数图象.稍等片刻,老师找出几份代表性的作业进行投影,暴露一些典型的错误(有的没有画出渐近线;有的图象在一个周期内出现两个端点……).教师利用多媒体,展示标准的作图过程. 追问1:由正切函数的图象,我们可以得到哪些性质? 众生:(1)定义域;(2)值域;(3)奇偶性;(4)周期性;(5)单调性;(6)对称性. 生:不可以,因为图象不连续. 师:对!我们应强调每一个区间上函数保持单调递增. 追问3:对称中心为(kπ,0)(k∈Z),对吗? 3.学以致用,主动出击 师:根据性质,你可以提出哪些问题?(由学生讨论共同得到如下问题) (2)函数y=tan 2x的周期; 4.总结思考,提高能力 (1)正切函数的图象作法; (2)正切函数的性质; (3)正切函数的应用; (4)感受数形结合思想和整体法的应用. 1.两种设计的异同点 这两种设计的共同点都是基于学生现有的知识储备,在学生最近发展区来设计问题;问题的设计突出了教学重点,能充分挖掘学生潜能,调动学生主动探究的积极性,生生互动,师生互动较好;学生围绕问题展开思考、讨论,教师针对教学难点设计了一系列追问,并在学生反馈的基础之上加以引导和点评,使得本节课的教学难点在无形之中得以化解.总体上,这两种设计都是有效的.比较来看,也有各自独特的地方.第一种设计思路是先由前面的知识推导出正切函数的部分性质,以已掌握的部分性质为基础去研究正切函数的图象,接着再解决未知的性质,体现了由性质——图象——性质的流程,整个设计贯穿了一条由数——形——数的思维过程.第二种设计思路是由函数的图象到性质,整节课围绕如何作图,在反馈、示范以及规范作图方面处理细致入微,使得课堂重心前移,后面正切函数的应用没有得到充分展开. 2..根据教材的编写意图来审视本节课的教学设计 通过研究教材我们发现,正切函数的学习是放在正、余弦函数之后,前面的知识和研究方法为本节课的学习提供了经验.利用三角函数线作正切函数图象是本节课的重点也是难点,大多数学生已经了解该方法,本节课不必大动干戈.几何作图的方法和流程设计上可以淡化,不应成为本节课的重心,第二种设计显然已经偏离了教材的意图.第一种设计没有必要就描点作图设计过细,总结过多,纠缠不清,影响了后面时间分配,导致整节课前松后紧. 3.基于学情来考量两节课的教学设计 如果将教学的设计思路发散一下,我们大体上可用三类方式展开.一类是研究函数的一般思路,由图象到性质,再到应用;第二类是由性质到图象,再到性质;第三类是由性质到图象.比较而言,第一种方式虽然是教材的一厢情愿,但毕竟正切函数的图象不同于正、余弦函数,对学生来说,正切函数图象的作法是有难度的,一开始就作图,显得生硬,摸不着头脑.第三类设计方式,老师需要先引导学生利用已学知识推导出性质,尤其正切函数的单调性值域需要用到正切函数线来探求,对学生的能力要求较高,一般要慎用此种设计.第二类设计先推导出部分简单性质,这样为作图提供知识基础,化解了作图的难度,作好图象后再利用图象讨论性质,使得对性质的理解升华.这种设计既贴近学生的最近发展区,又自然,学生的参与度高,体验深,效果好.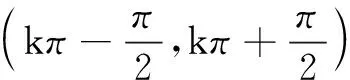

二、教学实录二





三、两种教学设计的比较和思考

