由整体性解决一类与函数零点有关的问题

林志敏 黄永生

福建省泉州市第七中学 (362000)

解决函数零点问题的关键是如何把函数的零点、方程的根、曲线的交点的横坐标三者进行转化.不同的问题，突破口也有所不同，有些零点问题，特别是含参问题，从单个零点入手有困难，此时利用整体性，问题通常就能迎刃而解了.而且解决过程中，通常结合下面三个结论，往往会提高解题效率.

①函数y=|logax|与直线y=k有两个不同交点A(x1,y1),B(x2,y2)，则x1x2=1;

②函数f(x)关于直线x=a对称且在(a,+∞)上单调，则x1+x2=2a⟺f(x1)=f(x2);

③函数f(x)关于点(a,b)对称且在定义域上单调，则x1+x2=2a⟺f(x1)+f(x2)=2b.

本文例举几题予以说明.

例1 若x1满足x+2x=5，x2满足x+log2x=5，则x1+x2=( ).

例2 设x1,x2分别是函数f(x)=x-a-x和g(x)=xlogax-1的零点(其中a>1)，则x1+4x2的取值范围是( ).

A.[4,+∞)B.(4,+∞)

C.[5,+∞)D.(5,+∞)

例3 已知函数f(x)=

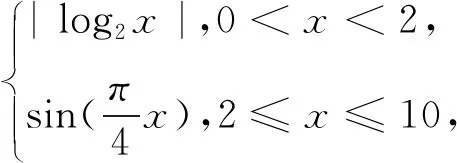
A．(4,16)B．(0,12)

C．(9,21)D．(15,25)

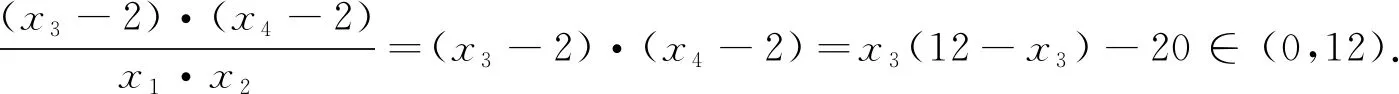
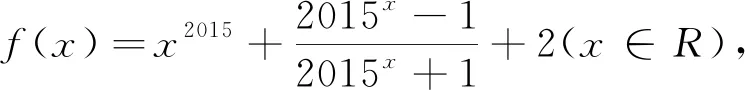
A.1B.3C.4D.9

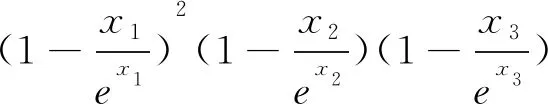
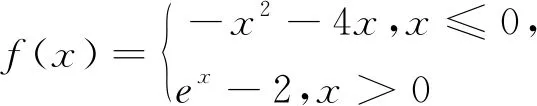
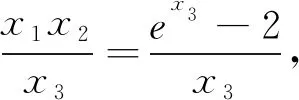
由以上实例可知,利用整体性解决有关函数零点求值及范围问题，关键是根据题目条件，找到零点之间的内在联系，可以直接求值，也可以消元简化问题再求解.