从一道函数零点试题管窥函数与方程的教学*

陈小红

江苏省常州高级中学 (213003)

函数描述了自然界中量的依存关系，是对数学问题和实际问题中数量本质特征和制约关系的一种刻画．方程与函数是密切相关的，并且相互为用，如解方程f(x)=0就是求函数y=f(x)的零点，也就是求函数y=f(x)的图象与x轴的交点的横坐标．而函数与方程在现行高中教材中是以知识内容和思想方法两种不同的形式来呈现的，函数与方程教学也要不断地在函数与方程问题之间转化，体现了较高的灵活性，同时也有一定的复杂性．本文以一道函数零点试题为例，通过对它的多种解法的解读，谈一谈对函数与方程的教学启示．

题目已知a,b∈R，若存在b∈[-3e,-e2]，使得函数f(x)=ex-ax-b在[1,3]上存在零点，则实数a的取值范围为．

解法1：设g(x)=ex-ax，其中x∈[1,3]，且g(x)的值域为A，设集合B=[-3e,-e2]，则A∩B≠Ø．因为g(x)=ex-ax，所以g′(x)=ex-a．

当a≤e时，g′(x)>0对x∈(1,3)恒成立，且g(x)在区间(1,3)上单调递增，又g(x)在区间[1,3]上图象不间断，则A=[e-a,e3-3a]⊆[0,+∞)．此时，A∩B=Ø，矛盾；

当a≥e3时，g′(x)<0对x∈(1,3)恒成立，且g(x)在区间(1,3)上单调递减，又g(x)在区间[1,3]上图象不间断，则A=[e3-3a,e-a]⊆

(-∞,e-e3]．此时，A∩B=Ø，矛盾；

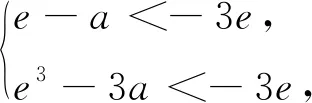
综上所述，实数a的取值范围为[e2,4e]．

点评1：在解法1中，因为参数a影响函数g(x)的单调性，因此g(x)值域的表达形式也应分成三类，其中两类可通过观察得g(x)的值域与区间

[-3e,-e2]无公共元素．在第三类中，g(x)的值域与区间[-3e,-e2]有公共元素的情形比较多，但其反面情形比较少，所以可以先考虑反面，即使用“正难则反”的运算策略．利用集合的运算来解决这个问题关键是集合运算模型的建立，而难点是已知含参集合与区间[-3e,-e2]有公共元素求参数a．

解法2：原条件等价于不等式-3e≤ex-ax≤

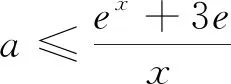
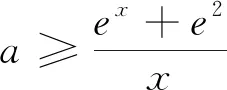
图1

结合前面两个方面，可以知道e2≤a≤4e．

当e2≤a≤4e时，结合g(x)和h(x)的图象(如图1所示)知，直线y=a必定与g(x)和h(x)中的某函数的图象相交，如图1中的交点P的横坐标就是不等式g(x)≤a≤h(x)的一个解．综上所述，实数a的取值范围为[e2,4e]．

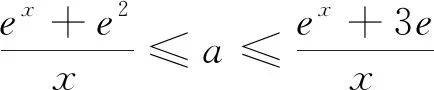
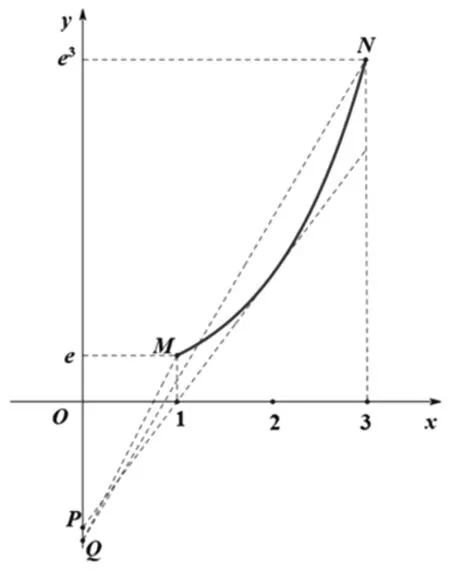
图2

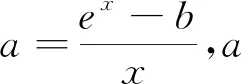
点评3：在解法3中，要注意以下几点：其一，当固定曲线段MN上一点时，该点与点Q的连线的斜率大于该点与点P的连线的斜率，所以求斜率a的最大值，即求点Q与曲线段MN上点的连线的斜率的最大者；求斜率a的最小值，即求点P与曲线段MN上点的连线的斜率的最小者；其二，求斜率a的最大值，一定要注意比较MQ与NQ的斜率的大小，这是因为指数函数的增长速度比较“快”，如果不借助于几何画板等数学软件作图，很可能会求错最大值，比较这一过程恰能体现了“数形结合”中“数”的精确性．

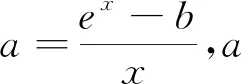
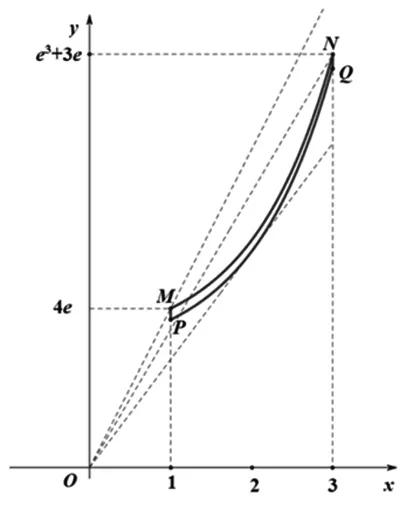
图3

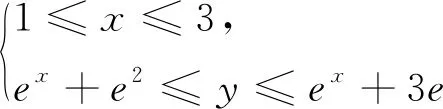
点评4：解法4可以认为是解法3的改进，曲线段的上下平移恰好扫过一个平面区域．解法4斜率模型的建立要比解法3中的斜率模型的建立难度更大一些，但更容易理解．

结合前面的几种解法，笔者对函数与方程的教学提出了以下几点启示：

第一、注意常见模型的积累，灵活运用模型，实施转化化归．

这里的模型是指解特定数学问题的一种数学框架或结构，或常见的某类问题．例如，解法1转化成了集合运算的模型，即已知两个集合交集非空，求参数问题；解法2转化成不等式有解的模型，最终转化成求函数的最值问题；解法3和解法4转化成直线的斜率模型，通过分析直线的动态变化，求斜率的取值范围．

第二、注意数形结合的运用，重视形的直观，重视数的精确．

在思考和解决函数与方程的有关问题时，对于某些从表面上看来，与图形不相关的问题，有时可以从某种特定的角度，画一个图形、图象或示意图，把所讨论的问题给以几何直观地描述，往往会对问题的求解提供很多有益的启示，借助图形常常可以把问题中的数量关系揭示得更加直观形象，“图”可以帮助思考，把抽象的东西变得直观，从而使得解题思路变得简单明了．从前面的解法2的检验过程、解法3和解法4都能体会到图形的直观性，易于问题的解决．但比较突出的一个问题是，对函数与方程的教学，不少教师侧重于用形来处理数的直观性，而用数处理形的精确性往往被忽视，学生也往往忽视．例如，笔者与一个学生交流时，发现学生采用的是解法3解决的，直接画了一个示意图(画出的指数函数图象增长的速度“较慢”)，没有与NQ的斜率进行比较，就直接认定MQ的斜率就是最大者．虽然结论也是对的，但具有偶然性．因为指数函数增长的速度“很快”，所以需要比较两斜率的大小，否则很容易出错．笔者尤其记得一个填空题极为典型，即问方程2x=x2的解的个数时，不少同学觉得指数函数增长速度比二次函数增长速度“快”，随手画了示意图，得出两图象有一个公共点，即解的个数为1的错误结论．利用数来辅助对形的认识，也是数形结合的一个重要方面，应引起重视．加强对“数能入微”价值的挖掘，对培养学生缜密的思维习惯大有裨益．

第三、注意转化化归的等价，分析前后关系，防止逻辑偏差．

转化与化归几乎贯穿于数学解题的始终，函数与方程的问题的解决也不例外．但是值得注意的是，要关注转化的等价性，分析转化前后的关系，防止出现逻辑偏差．很多时候，有一些不等价的转化较为隐蔽，不容易被发现，逻辑上会出现差错．

常见的逻辑偏差包含以下两种情形但不局限于这两种情形：其一，不能理解条件的充分必要性导致的所求范围扩大是比较常见的逻辑偏差．例如解法2中需要有检验的过程实质上就是检验a的范围的充分性．而这个检验过程是必要的，理由如下：关于x的不等式h(x)≤a≤g(x)在[1,3]上有解，可以得到两个不等式h(x)≤a，a≤g(x)在[1,3]上有解，这是从整体到局部的推理，从不等式组有解可以推出两个不等式有解，因此这个转化是正确的．但这个转化不一定是等价转化，因为从两个不等式h(x)≤a，a≤g(x)在[1,3]上都有解，不一定能得到h(x)≤a≤g(x)在[1,3]上有解．例如，若h(x)≤a在[1,3]的解集与a≤g(x)在[1,3]的解集的交集为空集时，h(x)≤a≤g(x)在[1,3]上一定无解．其二，不能准确地转化含有量词(尤其是含有多个量词)的某些条件也会导致逻辑偏差．含有单个量词的条件的转化相对比较容易，例如不等式恒成立或有解问题，往往可以转化成求函数最值问题，方程有解问题可以转化成求函数值域问题等．含有两个及以上的量词的条件相对比较困难，前面的例子含有两个存在性量词．一般来讲，可以先转化其中一个量词，得到一个新的只含一个量词的条件，再考虑另一个量词的转化，最终转化成不含量词的条件．