学会“选择” 绽放“精彩”
——一道高考题的教学反思
何雪冰
江苏省江浦高级中学 (211800)
在考场上如何选择合适的解题方法?这是学生必须要思考和面对的问题.在高三二轮复习课上笔者选择了一道高考题,选用四种具有代表性的解法进行了讲评,对所选的方法进行了比较分析,取得了较好效果.数学教育家弗赖登塔尔说过:“数学是人的一种活动,如同游泳一样,要在游泳中学会游泳.我们也必须在数学中学会数学.”
1.原题展现
(2019年江苏卷第12题)如图1,在ΔABC中,D
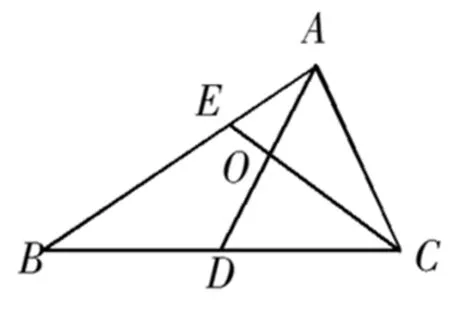
图1
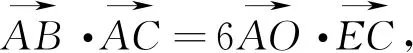
2.错因分析
(1)向量较多,没有思路或思路太多,无处入手,基底思想理解不深刻;(2)分点O的位置不明确,直接猜测;(3)字母较多,线性运算或坐标运算不正确,运算能力薄弱;
3.解法透析
3.1基底思想,坚定不移
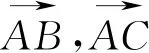

解法反思:这种方法是解决此类向量问题的通性通法,本题困难在于线段AD上分点O的位置如何确定.利用向量基底的思想,恰当选择一组不共线的向量为基底,通过线性运算将平面内所有向量转化为基向量,利用向量共线定理和平面向量基本定理建立联系确定参数的值.
3.2 建立坐标,化险为夷

图2
解法2:如图2建立坐标系,不妨设C(2,0),A(3a,3b),则D(1,0),E(2a,2b),直线AD的方程:y=

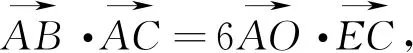
评析:通过建立直角坐标系,将思维量转为运算量,降低本题的思维难度,利用点坐标、直线方程等代数手段刻画图形关系,从而建立向量坐标的等式,最终得到线段AB,AC长度的比值,这种方法也是解决向量问题的常用方法.
3.3 方程视角,别有洞天
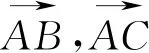
评析:方程视角给这道题注入了一股清风,让人耳目一新,转化为角θ的等式可谓是水到渠成.这个解法告诉我们,知识与方法是相辅相成相通的,可以充分发挥各自优点,服务于解题.

图3
3.4 巧作平行,意外惊喜

评析:这一道题的背景实际上是初中的一道平面几何问题.解决这类问题,既要想到平面向量的知识,也要想到平面几何知识,有时可能会起到事半功倍的效果.
4.解法辨析及反思
结合这四种方法,学生在课堂上展开了热烈的讨论,到底哪一种方法好?得到如下结论:

视角知识与方法优点缺点向量基底基底化思想、共线定理、平面向量基本定理通性通法线性运算要求高坐标坐标化思想,设点坐标、直线方程易于入手,降低思维计算较复杂方程齐次化思想、方程恒成立减少运算不易想到平面几何平行线段成比例减少运算读图要求高
学生经过了高三两轮复习,已经系统地回顾了高中数学知识与方法,但是看问题不知道从哪入手,也不知道使用哪种解题方法,这背后是因为学生思路与方法的混乱,没有形成清晰的知识脉络.因此我们要想学生所想,顺学生所思,在学生解决问题的过程与方法中发现问题,及时梳理,帮助学生确定解题的方向和视角.尽可能给出多种不同解法,这样学生才能在面对问题时会有多种选择的方法.通过对“个问题”的研究,回顾与深化相关的知识点及解题思想方法,从而让学生达到对“类问题”的解决,也就是我们通常说的让学生通过一题多解,最终实现多题一解.教师平时教学要善于方法的总结与优化,引导学生学会主动归纳总结典型问题的各种解法,并掌握处理问题的通性通法.在掌握基本方法的同时,还要让学生学会分析、比较,优化解题方法.这样当学生遇到不同问题时,才会选择恰当的方法,少走弯路.

