基于EMD分解重构的1-NN-SPMDTW时间序列分类方法
唐登林 陈毅俊
(1.贵州商学院财政金融学院 贵州 贵阳 550004;2.贵州商学院财政金融学院 贵州 贵阳 550004)
时间序列是一种普遍存在的数据类型,对时间序列数据的挖掘是目前的研究热点之一,其中时间序列分类(Time-series Classification,TSC)问题吸引了众多学科的研究者,出现在了包括数据挖掘,医学,金融学,统计学,机器学习,信号处理,环境科学,计算生物学,图像处理,化学计量学等众多研究领域.
一、相关工作
以DTW为基础的TSC算法存在的主要问题是DTW计算量很大、耗时较长,同时在理论上看,分类精度存在着改进空间.有关加速DTW分类速度和提升分类精度的研究可以概括为以下三个方面:一是,通过改进传统的DTW技术,设计新的DTW技术并与1-NN算法或其他分类算法相结合,如文献[1-4].二是,因为弯曲窗口(Warping Window)的大小影响着DTW的搜索空间,因此寻找最优弯曲窗口可以提升计算的速度,同时相对紧凑的弯曲窗口能够提升分类精度[20].例如,文献[21]利用搜索范围下边界查找表和根据斜率推导上边界的方法,控制搜索路径,在一定程度上提高了运算效率.文献[22]提出了基于DTW距离和时间距离的双距离最佳弯曲窗口学习方法,文献[23]将全局约束与提前终止技术相结合建立了动态弯曲窗口,文献[24]利用启发式搜索方法为每一类别的时间序列寻找最优弯曲窗口边界.三是,将传统DTW与其他算法相结合,如文献[18]利用数据块消减技术减少训练数据从而提高1NN-DTW分类算法的速度,文献[25]将序列分段方法与DTW相结合,提出了特征点分段弯曲时间距离,文献[26]在不考虑计算时间的情况下,将测试集样本与每个训练集样本的DTW距离作为支持向量机(SVM)的输入特征值,并与符号聚合近似法(SAX)相结合提升了TSC分类精度.文献[27]先利用分段聚合近似方法(PAA)对数据降维,将原序列转化为时序段平均值序列,然后计算DTW距离.
以上研究工作拓展了DTW技术在时间序列数据挖掘上的应用,为本文的研究奠定了理论基础.本文提出的基于EMD分解重构的1-NN-SPMDTW时间序列分类方法,首先运用EMD分解重构曲线良好的去噪能力,对时间序列进行平滑处理,并利用特定的方法找到关键极值点;然后在一定坐标间隔阈值以内,采用特殊点对选取规则对两两时间序列的极值点进行匹配,相互匹配的极值点称为特殊点对;最后以计算的特殊点匹配DTW距离作为相似性度量,并结合最近邻算法实现分类.该方法操作简单,可调参数少,在适当的参数设置下能够实现时间序列分类精度和计算速度两方面的提升.
二、背景知识
在本节中,我们主要介绍动态时间弯曲方法和动态弯曲距离的相关知识,并对EMD分解和重构做简要阐述.
(一)动态时间弯曲(dynamictimewarping)
给定两个时间序列,Q={q1,q2,…,qn}和C={c1,c2,…,cm},其长度分别为n和m.事先定义一个n行m列的距离矩阵D,其中元素dij=d(qi,cj)=(qi-cj)2表示qi和cj之间的距离.W={w1,w2,…,wK}(max(n,m)≤K≤n+m-1)是一条弯曲路径,元素wK=(i,j)表示序列Q中的qi与序列C中的cj相匹配.弯曲路径定义了Q和C之间的一种映射关系,并且满足以下两个约束条件:
边界条件:w1=(1,1),wK=(n,m),即要求W起始于距离矩阵的左下角,终止于右上角.
单调连续条件:若wk=(a,b),wk-1=(a′,b′),则0≤a-a′≤1,0≤b-b′≤1.这要求W在时间上只能向前发展,并且每次只能增加0或1.
满足以上条件的弯曲路径存在多条,我们寻找一条累计距离最小的路径,称之为DTW路径,其值为DTW距离.
(1)
DTW距离可通过动态规划方法求得:

(2)
计算DTW距离时的搜索空间需要遍历整个距离矩阵D,因此计算需求较大,复杂度为O(n*m).
(二)经验模态分解(empirical mode decomposition)
经验模态分解(EMD)是一种时频处理算法,能够根据数据自身的特征通过迭代的方式自适应地获取基函数和分解层次,特别适用于非平稳、非线性数据的处理[28].
EMD算法的目的是将复杂数据分解为若干个本征模函数(IMF),每个IMF刻画了原数据不同时间尺度上的特征.IMF必须满足以下两个条件:(1)函数在整个时间范围内,局部极值点和过零点的数目必须相等,或最多相差一个;(2)在任意时刻点,上包络线和下包络线的平均值必须为零.
EMD方法的分解过程如下:
(1)找到x(t)的所有极大值、极小值点并在极值点间用三次样条函数进行插值,得到上、下包络线emax(t)和emin(t).
(2)计算上下包络的均值m1(t)=(emax(t)+ emin(t))/ 2,从x(t)中减去m1(t)得到第一个分量d1(t),即:d1(t)= x(t)- m1(t).如果d1(t)满足IMF的两个条件,则IMF1(t)= d1(t);否则,把d1(t)看作新的数据,其包络平均值为m11(t),得到d11(t)= d1(t)-m11(t),重复这个“筛分”过程k次,直到第k次的d1k(t)是本征模函数,则:IMF1(t)= d1k(t).
(3)原数据x(t)减去第一个本征模函数IMF1(t),则得到一个新数据序列r1= x(t)-IMF1(t),对r1进行如上所述的“筛分”过程,这样不断重复便可得:r1-IMF2(t)= r2,…,rn-1-IMFn(t)= rn.当余项rn是一个常数或者单调函数,不能再分解出本征模函数时停止分解,则有:
(3)
分量IMF1(t),IMF2(t),…,IMFn(t)分别包含了数据从高到低的不同频率成分,而rn则表示了原数据的中心趋势.文献[29]提出对信号EMD分解后得到的本征模函数分量重构原数据可以达到消噪的目的.由于噪声大多数存在于低阶IMF里,所以可以根据实际需要将若干个高阶IMF分量以及余项rn进行叠加,得到重构数据,实现去噪处理。公式为:
(4)
三、利用EMD分解重构的曲线寻找特殊点对
由上一小节可知,“合理的”特殊点对的引入能提升速度和精度,因此特殊点对的选择十分重要.极值点作为时间序列中较为重要的点,蕴含着时间序列的重要信息,是研究者们较为关注的一类点.由于噪声和异常值扰动等原因,时间序列往往存在多个极值点,因此并不是所有的极值点都有意义,需要过滤掉那些没有意义的极值点.如文献[30]利用重要性标志算法(EIIR)和极值点判断算法(JEP)来寻找极值点.本文利用EMD分解重构曲线寻找有意义的极值点,是一种较为新颖的方法.为了叙述方便,我们称“有意义的极值点”为“特殊点”.
将EMD分解后的IMF进行重构时,应当确定选取哪些IMF分量和选取的数量.很多学者提出了不同的方法和选择标准,如皮尔逊相关系数.我们利用EMD方法的目的是通过EMD分解重构在众多的极值点中找到数量较少的有代表性的极值点,因此我们利用公式(4),通过简单地叠加若干个高阶IMF重构出EMD曲线.以ECG200数据为例,原序列x(t)以及重构的x11(t)、x12(t)和x13(t)的曲线如图4所示.为了便于观察,我们将x12(t)和x13(t)分别向下平移了1个和2个单位.
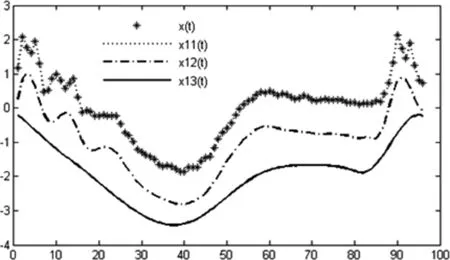
图1 ECG200的原序列和重构序列
在图1中我们发现,重构的x11(t)就是原序列x(t);与原序列x(t)相比,x12(t)较为平滑,极值点数量变少,能够较好地还原x(t)的性质;x13(t)极值点数量更少,但是其极值点的坐标与x(t)存在一定的偏差.因此我们考虑将x12(t)和 x13(t)各自的优点相结合,使如下过程找到x(t)中的特殊点.
找到x13(t)曲线上所有的极值点坐标,若点A为x13(t)的一个极大值,坐标为maxA,其相邻的前后两个极小值坐标为minA1,minA2,则在区间[(minA1+maxA)/2,(maxA+minA2)/2]内寻找x12(t)曲线上的极大值点和最大值点(若点A为序列中出现的第一个极值,则minA1=1,为序列的左端点坐标;若点A为序列中出现的最后一个极值,则minA2等于序列的右端点坐标).若此区间内某一极大值同时为最大值,则该点为极大值特殊点,否则此区间内不存在特殊点.同理,若点B为x13(t)曲线上的一个极小值,坐标为minB,其相邻的前后两个极大值坐标为maxB1,maxB2,则在区间[(maxB1+minB)/2,(minB+maxB2)/2]内寻找x12(t)曲线上的极小值点和最小值点(若点B为序列中出现的第一个极值,则minB1为序列的左端点坐标;若点B为序列中出现的最后一个极值,则minB2等于序列的右端点坐标).若此区间内某一极小值同时为最小值,则该点为极小值特殊点,否则此区间内不存在特殊点.
利用这种寻找过程可以找到任意单个时间序列中所有的极大值特殊点和极小值特殊点,所找的特殊点数量不超过x13(t)曲线的极值点数量.因此,IMF叠加的数量以重构曲线的极值点数量作为判断标准.为了便于描述,我们将利用x12(t)和x13(t)寻找特殊点的过程,记为“x12(t)←x13(t)”.若x13(t)中的极值点数量较多时,我们有两种方法可以选择,一是舍去x13(t)中坐标间隔小于一定数值的极值点,二是利用x12(t)和x14(t)来寻找特殊点,即“x12(t)←x14(t)”,寻找过程相同,不再赘述.
单个时间序列中特殊点分为两类,分别是极大值特殊点和极小值特殊点,当计算两个时间序列的SPMDTW距离时,将某一时间序列的极大值特殊点与另一时间序列的极大值特殊点相互配对,形成极大值特殊点对;将该时间序列的极小值特殊点与另一时间序列的极小值特殊点相互配对,形成极小值特殊点对.为了避免病态匹配,造成不合理的结果,我们设定坐标间隔阈值(interval),只有在间隔阈值以内的极大值特殊点对和极小值特殊点对才能相互匹配.某些情况下,间隔阈值以内形成了该序列的一个极大值特殊点对应于另一序列的几个极大值特殊点,为了造成不必要的麻烦,舍去该区间内的所有配对.同理,适用于极小值特殊点对的匹配.我们将这种匹配规则称为特殊点对选取规则。

