我国国债利率期限结构的影响因素与投资组合策略的应用——基于主成分分析法和因子分析法

毛 魁

(河北地质大学 河北 石家庄 050031)

文献综述：

国内：王春风(2014)使用赫米尔特插值法，研究了中国债券市场的利率期限结构，量化了风险因素，得到债券组合管理的策略与风险对冲的原则，并进行实证分析，检验了模型的有效性。

吴迪(2019)验证了目标久期策略不随到期收益率的变动而变动，使用了中债全价指数创建模拟组合进行了策略的验证和推演，得到比较好的结果。

国外：Nawallcha和Soto(2009)将债券组合的利率风险对冲模型分为四类：

1.M绝对值模型/M平方模型

2.久期向量模型/M向量模型

3.关键利率久期模型

4.主成分(Litterman和Scheinkman,1991)模型(后面我们会涉及到该方法的应用)

上述的四个模型是在传统模型的基础上进行扩展得以研究。

一、债券组合投资管理策略

一般认为，债券投资组合管理策略会实时根据投资者对利率的预期和投资者对市场的态度分为消极和积极的投资组合管理策略，之所以会形成两个截然不桶的策略，是由于投资者或者金融机构对于市场的态度。如果投资者认为市场不是什么时候都有效的，一定存在盈利空间，那么就会选择积极的管路策略；反之，会选择消极的管理策略。

(一)积极的债券组合投资管理

此策略主要是由于金融机构认为可以对利率进行相应的预期，以此来战胜金融市场，通过不断地调整金融资产投资的比例，以此达到获利的目的。除了对利率可以进行预期还需要几个相应的前提条件：

1.债券市场弱势有效或无效。从具体来讲就是说，只要市场是弱势有效的，那么在市场中总能找到活力的机会，也就是存在被低估的债券，或被高估的债券。此时就会出现低买高卖的情形，出现获得利润的时机。

2.超额收益的来源：对利率进行预测是最主要的来源之一，另外的一种就是找出定价错误的固定收益证券。和第一个条件相吻合。

积极的债券组合管理策略要求金融机构和投资者准确地把握利率走势，加上积极、合理地调整相应债券地投资比例。积极的债券组合管理策略策略的要求的条件比较多，而且需要身后的专业知识来达到这种策略，所以会比较的繁杂，也只有金融机构如银行，保险，基金等才能大致的对市场利率进行预测，因为他们的得到的信息比一般投资者更有效和更充分。

(二)消极的债券组合投资管理

消极的债券组合管理策略的金融机构认为无法战胜市场，我认为可以把它成为比较稳妥的债券组合管理策略。之所以这样认为是因为这种组合管理策略对利率的变动并不是很敏感，而且负债和未来的现金流会相互的产生抵消，盈利或者亏损的限度低。净价格效应，和净利息效性产生的总效应的差值并不是很大基本可以相互抵消。

该策略主要的分类：一是负债管理策略，主要包括免疫策略和现金流匹配策略。免疫策略分为目标期免疫策略、多起免疫策略，和净资产免疫策略。现金流匹配有一个重要的特点是不考虑利率再投资的风险。免疫策略的利率会进行再投资，所以会有一定的利率风险，考虑的是将来某个负债到期是，所投资的债券组合能否应付将来时间点的负债。通过一定的计算和观察，要求两个条件。一是债券未来现金流的折现等于负债现值；二是债券组合的久期和负债的久期相等。这两个条件是实现目标期免疫的充分条件。而多期免疫和净资产免疫同样部分适用。总的来讲目标期免疫就是利用未来时间点的负债和未来时间点的资产相匹配，尽可能使资产大于或等于负债的情况。二是指数策略。顾名思义就是使债券组合和某个市场指数相挂钩，那个这个市场的跌涨起伏将直接影响该债券组合的投资比例。且如果该指数包含太多的券种，那么对金融机构来会更加难以管理，有时会失去投资的意义，达不到免疫的目的。

所以不管是积极的管理策略还是消极的管理策略，都会出现不理想的情况，消极的管理策略主要是挂钩某个基准，使它与基准之间的误差最小。积极管理策略则是在基准之外，积极主动地绕开基准，从而选择相对于基准更多的利率风险暴露，但到期收益率更高的债券来提高组合的相对收益，也就是我们说的高风险，高收益。

二、利率期限结构与相关理论介绍

(一)利率期限结构

利率是借贷资金的成本，利率期限结构是在某一个具体的的时间点上，利率随着债券期限变化的曲线关系。

上图是我国国债在2020年4月30日，以及一个月之前和一年之前的国债利率趋势图，横向来在不同时点上，不管是一年，一个月还是当下国债利率都随着到期期限的时长而增加；纵向来看，也是如此。符合我们国家国债的特点。

图2 数据来源：中国债券信息网

上图是选取了四个时间点上我国中债国债收益率曲线图，反映了不同时间点上国债利率的变化趋势。也能得出随着到期期限的延长，收益率增长的结论，同样符合我国国债收益率的特点。利率曲线结构有三种主要的变化趋势，上升、下降和水平，也可以两种或者两种以上相结合，反映了即期收益率与到期收益率之间的关系。

(二)利率期限结构的相关理论

1.市场预期理论。该理论由一些完美的假设，比如投资者没有投资期限的偏好，市场中不存在完全替代品，而相反，投资者一般偏好中短期债券，对利率的预期依据也比较简单，根据短期来不断的预期之后的利率，有一种惯性的思维方式。

2.流动性偏好理论。该理论是在利率预期理论的基础上提出来的，与预期理论的差别之一在于加了一个风险溢酬，由于持有期限过长存在利率波动的风险，为了补偿这个风险，需要加上一部分风险溢酬。

3.市场分割理论。该理论的缺点是把不同期限的债券市场看成各不相关的多个不同的债券市场，不同的债券市场有不同的利率期限结构。可以解释利率期限结构向上的趋势。

(三)利率期限结构的形状的影响因素

1.对利率的预期，是否向上或者向下或者趋于平缓的变动趋势。

2.债券收益中包含的风险溢酬，风险溢酬越大，则利率的越高，利率期限结构有向上的运动趋势。

3.市场的效率。根据有效市场假说理论，市场处于半强势、强势有效市场则技术分析与基本分析不会再发挥作用，那么就不存在套利机会，投资者对投资就会持有消极的债券组合投资。

三、国债收益率的期限结构分析

(一)模型分析

之所以选择国债收益率，主要是因为国债属于无风险利率。

用模型进行分析。Nelson 和 Siegle(1987)使用四个参数来描述整体收益率曲线形态，如式(1)所示：

(1)

其中，M 表示期限，r(M)为对应期限的债券收益。β0、β1、β2和 λ 为收益率曲线形态的参数，除了参数 λ 之外，其他三个参数都是线性形式。β0反映水平因素、β1反映斜率因素、β2反映曲率因素。这三个因素就是收益率曲线的三个主要的影响因素。

Diebold 和 Li(2006)对式(1)进行简化，将 λ设定为常数。将期限结构的变动 Δr(M)表达为 Δβ0、Δβ1和Δβ2 的线性组合。如式(2)所示：

(2)

接下来设定Δrt(M)=rt(M)-rt-1(M)，其中向量Δrt反映了不同期限国债收益率的变动。

从数据中摘选10种不同的期限(最短为 6 个月，最长为 30 年)。使用因子分析方法，可以将利率的变动表达为 Δrt=Lft，其中 L∈Rn×n为正交因子载荷，ft为n个因子向量。如果基于简化的N-S期限结构方程，利率的变动表达式为Δr(M)=HΔβt。H表示n*3的矩阵，n表示所选区的不同的期限，向量Δβt包括三个参数的变动即、Δβ1t、和Δβ2t。后来Memmel(2014)将Δrt=Lft(基于因子方法)和Δr(M)=HΔβt两个算式合并：证明得到下式：

Δβt=(L(1)’H)- 1ft,(1)

(3)

式(3)将基于因子方法得到三个重要因子转换成为期限结构方程的三个参数。就能够发现三个因子ft,(1)和三个参数的变动Δβt包含同样的信息，这样就可以用因子分析方法较好的拟合国债收益率曲线结构。基于上述分析，本文应用因子分析方法，对中国国债收益率的期限结构进行分析。因子分析将多个变量之间的相互关系，通过更少的几个公因子来描述。因子模型的矩阵形式为：

(4)

上式表示p个多元回归方程。Y1,y2,...,yp为可观测的变量，所对应的期望为υ1，υ2，...υp。矩阵表示因子载荷，F1,F2,...,Fm为不可关测的因子，ε表示未被因子解释的部分，即测量误差。

(二)利率期限结构的三个主成分影响因子

国外包括国内的一些研究普遍接受国债收益率的波动来源于两个或者三个因素的影响。Litterman和 Scheinkman(1991)将这三个因素归纳为水平因素、斜率因素和曲率因素。

1.水平因素也叫平移因子，顾名思义就是利率期限结构发生向上或者向下相同基点的平移，类似于数学中的平移，不改变利率期限结构的曲线形状。而且各个期限的因子的系数也就是(1)式中的β0。一般情况下，该因子可以解释利率期限结构变动的60%以上，我们从下表4就可以看出该因子78.93%的解释程度。

2.斜率因素，斜率因素是使利率期限结构变得平坦或者变得倾斜程度更大的主要因素，具体是曲线长的一端和短的一段变动不一致，短的一段上升则长的一段下降，此时出现变得变得平坦的情况。如果短的一端下降，而长的一段上升则利率期限结构会出现更大的倾斜程度。解释程度在5%-30%之间。表4的解释程度在15.23%，符合这个范围。

3.曲率因素亦叫凹凸因子，是使利率期限结构凹凸不一致的主要因子，该因子可以解释利率期限结构变动的1%-10%。表4的解释程度在3.1%同样也符合这个范围的解释程度。

水平因素对应于最大的特征根，如表4所示水平因素的特征根为10.26045，该数值反映出利率期限结构变动最主要的因素是水平因素，我们从图6的因子载荷图可以看出：水平因素影响下的收益率与到期期限的长短无关，水平因素对各期期限的利率影响程度相似。因此投资者可以在这种情况下进行套期保值，主要是利用久期/凸性使债券组合的价值不至于大幅度的变动。

倾斜因素对应于表4的第大二特征根，数值为1.979445，显然与水平因子差别很大，该因素的出现使短期和长期的利率发生不同程度和方向的倾斜。

曲度因素对应于表4的第三大特征值，数值为0.4026，该数值说明利率期限结构相比于第一、二大因子对利率的敏感性变得更低。

(三)主成分分析的原理与实证分析

原理：计量中的原理是说在被解释变量做回归分析时，各个解释变量对该回归的解释程度如何。比如有p个解释变量，我们做主成分分析，发现前三个解释变量就可以解释该被解释变量，此时我们就说，这三个解释变量就可以很好的解释被解释变量，还有一个条件，就是这三个解释变量的不存在相关性，以避免多重共线的情况。

下面所使用的数据来自中国债券信息网，从2002年实时发布日国债收益率数据，所使用的数据从2002年1月4日至2018年12月31日。选取的利率期限为1个月，2个月，3个月，6个月，9个月，1年，3年，5年，7年，10年，15年，20年和30年的国债即期收益率，样本包括了短期，中期和长期，包含了3746天的样本，国债收益率数据52444个，保证了数据的可靠性。下面我们逐一进行分析：

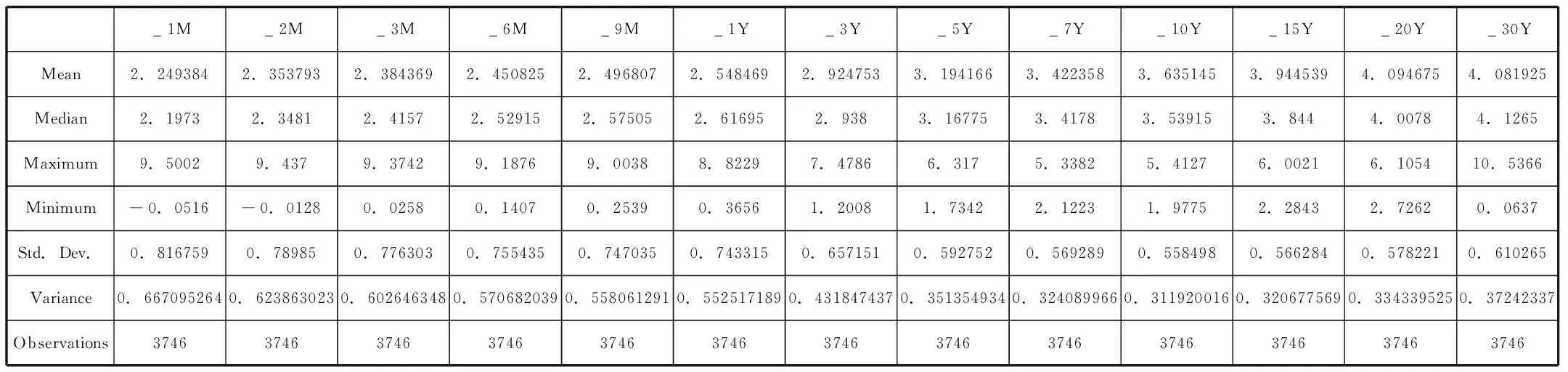
表1

上表显示了不同期限国债的的相关数据，均值，最大值，最小值，标准差，样本规模3736个。

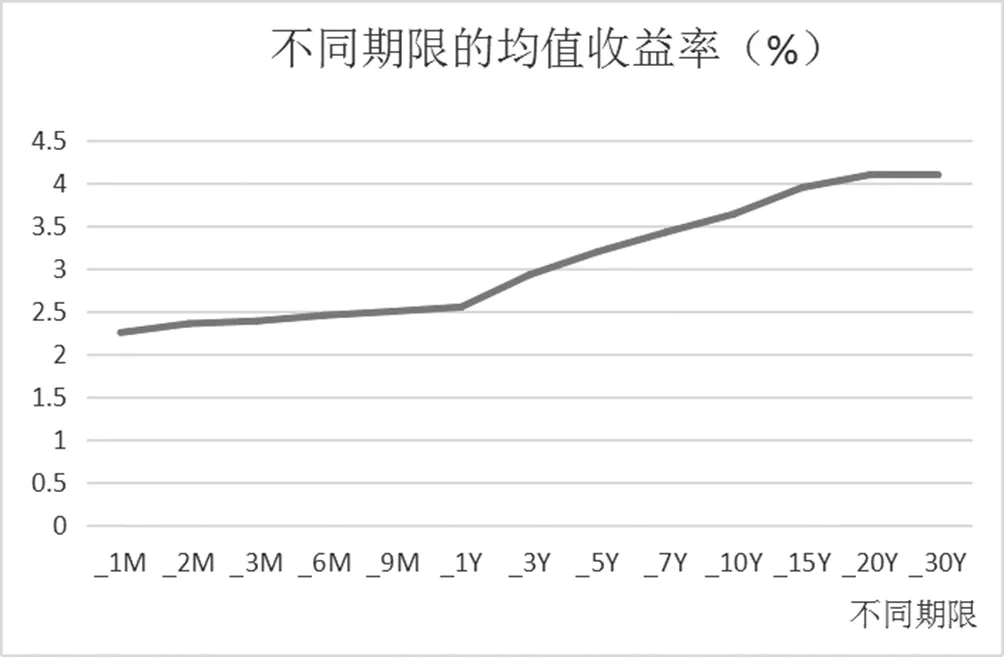
图3

如图3所示，不同期限的国债收益率债券呈现上升的趋势，即期限越长收益率越高的趋势。

图4

如上图所示，不同期限的国债收益率的方差也就是波动性呈现递减的趋势，即短期国债收益率波动性强，中长期国债收益率波动性弱的特点。这说明除了第一因子水平因素外，还存在其他影响收益率波动的因子。

表2 各变量之间的相关系数表

由表二的数据显示，国债之间的期限越是相邻，那么他们之间的相关系数就越大，也就是说相关性越强。总体来说各期限的相关性都比较强，可以做主成分分析。

表3 单位根检验

该检验说明02年到18年国债收益率是平稳的，Breitung t-stat等于0，下面检验三个值都小于0.05，表明各期限国债收益率是平稳的。

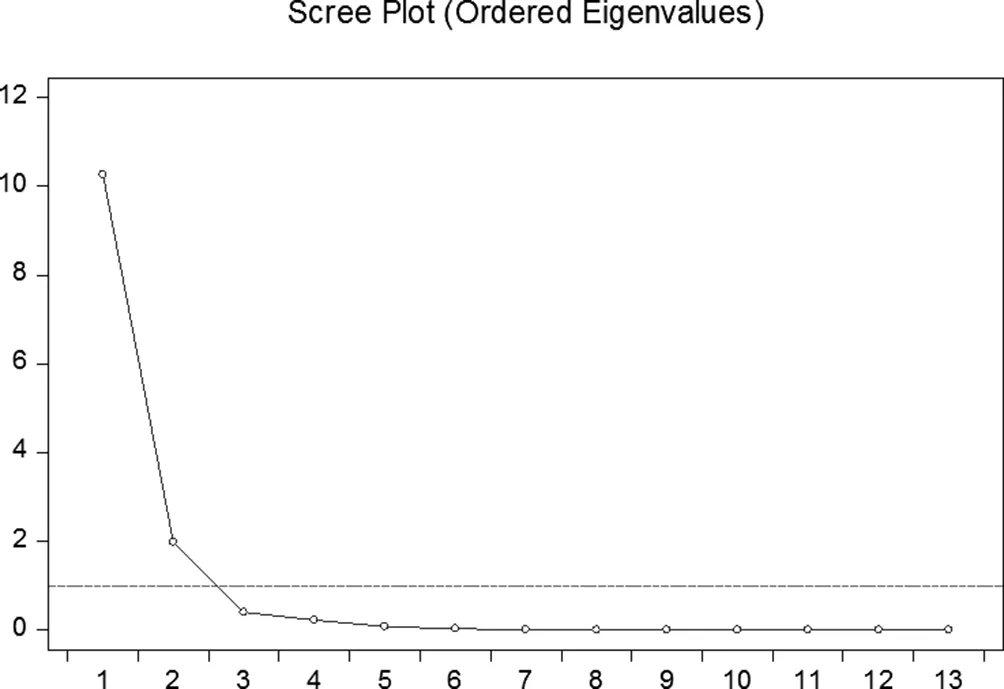
图5

如上图所示，横坐标表示主成分，从坐标表示特征值，从上图可以看出，第一个特征值位于最高点，反映了国债利率期限结构大部分的变化，第二个特征值接近2，次之。而第三个主成分已经位于坐标轴下方为负，就很难在某些程度上反应利率期限结构的的变化。因此选区前两个主成分就可以较为完整的反应利率期限结构的整体变动。

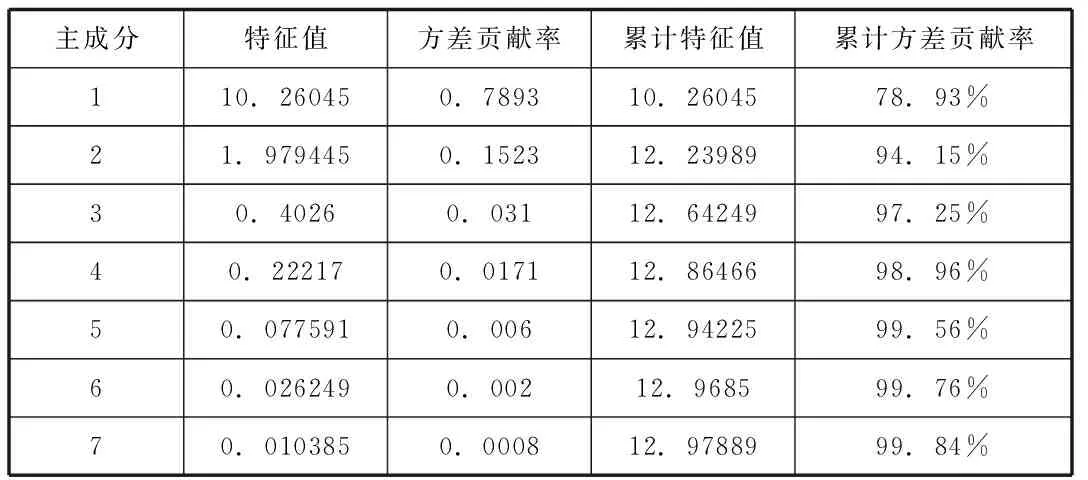
表4 各个主成分的方差贡献率

80.0061460.000512.9850399.88%90.0042920.000312.9893399.92%100.004080.000312.9934199.95%110.0030860.000212.9964999.97%120.0023550.000212.9988599.99%130.0011530.000113100.00%

上表反映了各个主成分对收益率总体方差的解释能力，第一个主成分解释收益率变动的78.93%，第二个主成分解释收益率变动的15.23%，第三个为3.1%，合计解释程度97.25%，可见我国国债收益率的三个主成分的累计解释力度接近发达国家水平。

表5 因子载荷量

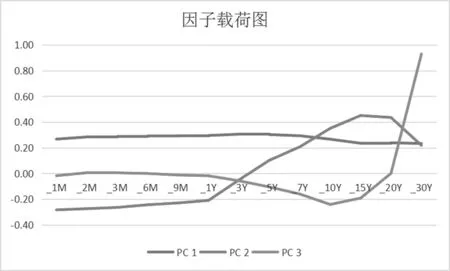
图6 各期限的因子载荷图

从表5和图6中可以看出，前三个主成分基本上对所有原始变量的方差变动的解释程度，都有较大的贡献。第一个因子，对所有期限债券的影响程度解释相似且显著，如上图蓝色的线条，基本上是一条直线，也就是我们说的水平因子；第二个主成分对1年以内的国债影响为负，对中长期国债影响为正，表示第二个斜度因子；第三个主成分对中短期的国债的影响为负，对长期国债的影响为正，表示取度因子。表示利率期限结构的三个主要影响因子主要就是上述的三个。

四、利率期限结构对债券组合管理策略的影响

关于债券组合管理策略，很多文章都涉及到一些比较好的免疫策略，一提到免疫当然就是消极的组合策略，比如利率风险管理的久期免疫策略，信用风险与利率风险的对冲策略，直接预测债券风险溢价的积极投资策略等等多种策略。我们来研究其中一种策略利率风险管理的久期免疫策略。

利率风险是债券投资面临的最主要的市场风险，简要的说就是债券投资者由于利率的变化，债券的价值升高或者降低的可能性。我们上面已经提到，免疫策略的相关内容，比如净价格效用与净利息效应的方向相反，相互抵消，以此来锁定一定的利润。我们就来实际应用这个策略看是否可以得到理想的结果。

久期是使用最广泛的利率风险的测量工具，与债券价格的变动与直接的关系。久期又是价格利率曲线的斜率，也就是一次函数，因此利率的变动直接影响价格的变动。久期越大，在某一时点变动时债券的价格波动越明显。

麦考利久期的计算公式:

n表示第n个付息期，Ct表示第n个付息的现金流，r表示市场中的折现率，现在把r调整为连续复利时：令r*=ln(1+r),带入久期的公式得到：

(5)

一个资产组合的久期就是组合内各项资产的久期的加权平均和，权重可以理解为各项投资占总投资的比例。

假设债券的投资者投资期限为N年，目标累计价值为Vn,那么该现值为:

(6)

同时我们把它转换为连续复利的形式：

V0=VN*e-rl*N

(7)

假设现在投资者把资金投资于一项资产组合，每年年末提供固定的现金流C1，C2,...,CN。

(8)

购买债券组合后，连续复利变化为Δr*。因为利率期限结构是平行移动的，所以目标累积现值和债券组合的现值利率变化是一致的。

目标价值的变动ΔV0:

Δv0=(dv0/dr*)*Δr*=[-N*VN*e^(-r*l*N)]*Δr*

(9)

同理债券组合价值的变动ΔVP：

(10)

如果V0=ΔVP,说明市场利率变化对投资者投资活动的效益不产生影响，也就是说是利率风险免疫的。和目标久期策略有一定差别。而且上述利率只变化了一次，显然这是不可能的情况。实际情况是市场利率每时每刻都在发生改变，所以就要在市场利率变化时，重新调整债券组合比重，使债券组合的久期等于剩余的投资期限，使债券组合对利率风险免疫。从中也可以看出，消极的债券组合投资策略同样需要不断地应对市场利率的变化，积极的调整债券投资组合的相关债券的比重才能达到保值增值，规避利率风险的作用。