实施“精准纠错”，实现“最多错一次”

周平儿

摘 要：只有找到了犯错误的位置、探明了错误的性质才能实现有的放矢，只有获取有效的得分分析数才能集中力量打歼灭战。只有充分调动学生的自主纠错意识，才能最终使精准纠错得到有效落实。

关键词：纠错;精准教学;数据;思维;说题

分类号：G633.6

1.直击现状：让人尴尬的错题集

抓住错题分析与提高，是很多教师提升教学质量的重要方法，由于实际操作中老师们普遍采取一刀切的做法，使得后进生面临大量的错题需要订正与反思，他们的学习负担可想而知。尽管有的教师也意识到了分层教学的必要性，但由于对于错误发生位置与方向上存在认识上的偏离，加之忽视学生的学习需求，使得错题集的使用存在很大盲目性。由于使用效果不理想，错题订正在不少学校依旧在走着上世纪九十年代时候的老路——讲解、订正、讲解……订正之后教师有时间就改一下，没时间就不改了，学生不管订正对错怎么样，基本上不再关注了。这样下去，作业的效果就难以保证。

2.对策思考：借助“数据多走路”，实施“精准纠错”

上世纪60年代，林斯利（Lindsley） 提出了“精准教学”这一名词，意在通过测量与评估来追踪学生的学习表现，以便实现针对性教学。但由于测量过程的繁杂化与数据收集真实性等问题，这一理论没有得到很好的应用。

“精准扶贫”是近年来国家帮扶弱势群体的政策。在扶贫过程中需要“扶真贫”，不贫的不能乱扶，这说明调研要精准;在扶贫的过程中需要“真扶贫”，不能隔靴搔痒，搞形式主义;“扶贫”要与“扶志”相结合，防止只发补助金，不给帮扶的错误做法。在数学教学过程中，错题信息的收集与订正，同样应该也必须杜绝“对牛弹琴”，走向“有的放矢”，从教师引领逐步走向学生自主纠错。“数据多走路，群众少跑路”，以便实现“最多跑一次”。借用这一理念，我们在分析错题之前应进行有效的调研，收集到充实的数据，开展针对性的分析，通过“调查细一分”来达到“错误少三分”的效果，最终向“最多错一次”的美好境界靠拢。

3.实践探索：化理想为现实

3.1落实错误位置，把握分析方向

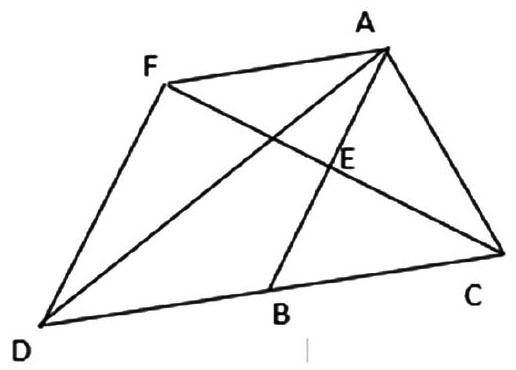
“打蛇打七寸”，只有抓住错误的要害，订正才能真实有效。如一次作业批改时，有这样一道题：如图：△ADC中，B是DC上一点，E是AB的中点，过点A作DC的平行线AF交CE的延长线F，且AF=DB.（1）求证：DB=BC（2）若AD=AC，试判断四边形AFDB的形状并说明理由。

获取数据：随机抽查10本作业，第（1）小题有8名学生借助证明△AFE≌△BEC实现了对DB=BC的证明，另2名错误的学生甚至较差。第（2）小题有8人判断为平行四边形，其中6名学生给出了充分的理由。有一人判断为菱形，写不出理由，显然他们忽视了条件AD=AC的应用。仅有1人正确判断为矩形。

采用随机抽查的方法，既避免了教师超负荷工作量，同时也精准地实现了对错误位置的把握：第（1）小题已经到了得分的极限，对2名不会做的学生只能暂时忽略，另行抽时间帮他们掌握三角形全等的知识。第（2）小题中，学生并没有完全把握图形的性质，他们发现了AD=AC这个条件，但由于图画中两条线段并不相等，他们怎么也得不到四边形AFDB是矩形的结论。正确画图成为有效解题的基础。在进一步的调查中得知：8个判断为平行四边形的学生中，其中有5名学生也是画过图的，他们直接在原图上尝试，拉长AC后却发现点E不再是AB中点了，只能作罢。

针对性策略：我讓答对的学生说说他是怎么画图的，他告诉大家，要先画草图，但要根据题目条件把可以画的等腰三角形先画出来，再逐步添加其它线段。由此可见，不良学习习惯的矫正与训练、程序性知识的习得与培养应该是错题分析的核心所在。经教师指导后，8个判断为平行四边形的学生中有7名学生已经能够独立画图并解答。

3.2探明错误性质，把握分析路径

同样一道题，学生的错误可能五花八门，但主要的错误原因是什么？我们可以按错误产生的来源分为知识性错误与过程性错误，可以按错误内容的性质分为纯数学错误与语言理解错误，可以按思维过程所属的性质分为概念错误、判断错误与推理错误。可以按学生的基础分为易于挽救错误与难以挽救的错误。比如上例中（2）的错误就属于过程性、纯数学、可挽救的判断错误。再如：

?ABC 是直角三角形， AB = 6， AC =8， 则 BC 的长度是                .

这道题大部分学生在解答时的答案只有一个“10”，这是典型的缺少分类讨论思想的表现，由于学生对于分类讨论的方法刚刚接触，做错也是难免的。抓住这是纯数学的过程性错误，教师可以引导学生写出解题思路：（1）如果BC是斜边，则BC=10。（2）如果BC只是一条直角边，那么BC=。此时要让学生明白：（1）什么情况下需要分类——问题情境所指不明确，存在多种可能;（2）如何分类——抓住一个固定的标准（这里是BC是否斜边）列举所有可能情况。由于这是第一次出现这样的错误，重点应该落在第（1）小点帮助学生建立分类的意识上，今后再出现同类题目时可把重点落在分类策略的指导上。

3.3获取得分数据，把握分析重点

过去，我校的普遍做法是备课组内搜寻出错误率最高的题目，然后教师自己寻找策略去讲解，但有的老师放心不下，恨不得把所有题目的解法都灌输给学生，最终难以达成良好效果。经过多年实践，我们认为得分率在40%-70%之间的题目最有提升价值，也应该作为教师讲解分析的重点。

根据传统的分层方法，对于 C 层次的学生，教师着重激发他们的学习兴趣，帮助树立学自信心 ;对于 A 层次的学生，教师可适当提高要求，让他们既有成就感，又会有压力感;对于 B 层次的学生，要让他们始终处于奋起直追的心理状态，促进他们不断取得进步。这样设定三个不同层次的评价标准，每次作业纠错仅针对学生处于最近发展区内的题目进行重点训练，使数学学习走向良性循环。

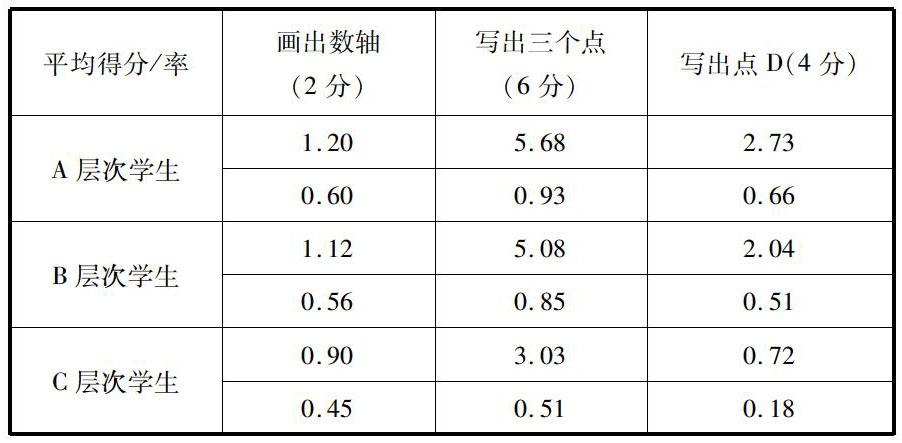
比如在学习数轴时，有这样一道作业题：一只蚂蚁从原点 O 出发，它先向右爬了 2 个单位长度到达点 A，再向右爬了 3 个单位长度到 达点 B，然后向左爬了 9 个单位长度到达点 C。 （1）写出 A，B，C 三点表示的数 ;（2）当蚂蚁位于点C位置时，一只蝗虫也在数轴上的D点上，且他距离蚂蚁正好是1.5个长度单位，那么蝗虫位置所表示的点是什么？

这道题并没有给出具体的图画，需要学生自行在作业本上补充出来。答题结果如下：

由表可见，学生对于画出数轴这一隐性的任务缺乏足够的意识，三个层次学生均处在40%-70%的区间里，所以必须重点强调。C层次学生还应该引导他们把握三个点的位置写法，A、B两个层次的学生需要重点引导写出D点。可见，精准的数据分析不仅是教师教学的依据与凭借，也是学生实现自我超越的利器。

3.4启动纠错意识，把握分析主体

学生学会分析科学的解题思路，是学生实现错误的精准有效订正的核心环节。近年来，我们形成了一套让学生自主说题的方法。

（ 1） 解题陋习具体化。“粗心大意”是学生的一惯缺点，但粗心背后的原因多种多样：有时是看错了题目信息;有时是思考问题片面，忽视了整体;有时是因为书写时答案抄错，事后检查又不充分。这些问题解剖不仅仅是针对学生自己，也是在不断提醒大家。

（ 2） 知识缺陷暴露化。“我以为…可谁知…所以就”——这是让学生自我陈述中常用的语言格式。学生在说题中大胆呈现错误，阐述正确的认知，使知识结构进一步得到重组，从而可以形成新的知识框架。

（ 3） 不当策略明朗化。让学生把解题时时的想方说出来，将有效提高他们对自己学习过程的反思能力。

（4）正确解法互动化。说题并不只始限于全班讨论，在说说正确解法这一环节，要充分运用小组合作的方法，大胆让学生去陈述、思考、争论，尽可能提升课堂的思维含量。

4.小结

只有找到了犯错误的位置、探明了错误的性质才能实现有的放矢，只有获取有效的得分分析数才能集中力量打歼灭战。只有充分调动学生的自主纠错意识，教会学生主动去反思与陈述错误形成过程，才能培养自主纠错的习惯，最终使精准纠错得到有效落实，也使“最多错一次”的理想變为现实。

参考文献：

[1] 王慧微.  初中数学错题本的作用与使用思路探讨[J]. 新课程（中学）. 2019（05）

[2]沈志斌，王玉家.学业诊断变革——以基础教育“极课学业诊断系统” 为例[J].教育，2016（16）：6-8