高中数学解题教学中逻辑思维培养

苏志成

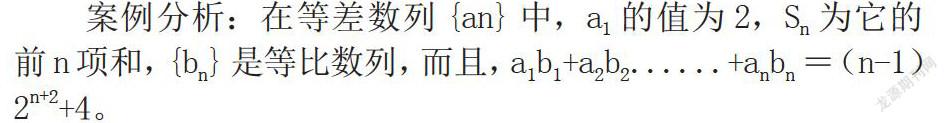
摘 要：就数学逻辑思维能力而言，主要是通过数学概念进行推理判断，从而对具体的数学问题进行处理和解决。在教学和与引导高中生数学解题时，其重點为三：其一，利用转化，实现“新旧知识”的转化;其二，基于深入探究，充分联想。通过旧知识衍生新知识。其三，对数学思想方法进行创造性的运用，以“新”带“新”，对新题型的生长点与切入点进行关注。

关键词：高中数学;解题教学;逻辑思维;数列解题

在教学高中数学解题知识中，数列解题为非常关键的一部分，所以，教师在课堂上需要把典型例题选择出来，通过转化、探索、反思三个角度引导学生把数列解题方法归纳总结出来，进而对学生逻辑思维的创造性、严谨性以及深刻性进行培养，而且还能够达到数学学科核心素养提升的目的。

一、推理解题法的运用，将思维严谨性提升

在教学数列知识时，有两种基本的数学——等差和等比数列，在解决大多数数列问题时，都离不开这两种数学形式而单独存在。即便是数列求和时，与它们也分不开。比如，倒序相加法就是在等差数列求和中生成的，还有错位相减法实在等比数列求和内生成的。所以，对数列解题进行整体观察，“转化”是它解题的核心思想，通过巧妙的引导学生转化，用已知问题转化出未知问题，如此一来，复杂的问题将会变得简单，很容易就解决了问题，而且，在转化期间，学生的逻辑思维能力也得到了加强，使其数学素养得到了显著提升。

比如，数列的恒成立以及通项问题，一般求解时，转化成函数最值和同性问题。

案例分析：在数列{an}中，a1的值是1，an+1的值是（an）/（an+3）.且n的取值范围为N※。求解：①、求该数列的通项公式;②对于，并且，Tn为数列{bn}的前n项和，如果对于所有的n为N※恒成立的条件，都能够给予满足，求解λ的范围。

从表面上看，这道题只对数列运算的内容进行了考查，实际上在问题内能够发现，数学逻辑推理内容非常丰富，前后联系密切，逐层递增，有效培养了学生的直观思维以及逻辑思维能力，显著提升了学生们的数学解题能力。

二、探究式题型的设计，把思维深刻性提升

在高考命题中，以数列为背景的探究试题逐渐增多，主要对学生数学创新能力以及数学思维能力进行考查，所以，在具体的解题标准内，我们也必须要足够重视这类问题。其问题类型有二：其一，新数列定义新题型。其二，存在性试题，此类问题不但对学生探究能力进行考察，并且，把一定的思维创新空间为学生留设了出来，而我们主要可以通过以下三类题型认识这类问题：探索规律问题;探索条件问题;探索结论问题。在课堂上，老师应该尝试把典型例题设计出来。基于典型例题，引导学生去剖析问题本源，通过思维把本质问题找出来，进而把学生的探究性思维发展和培养起来，进而提升他们的数学解题能力。

案例分析：在等差数列{an}中，a1的值为2，Sn为它的前n项和，{bn}是等比数列，而且，a1b1+a2b2......+anbn=（n-1）2n+2+4。

求解问题：把两个数列的通项公式求解出来。研究发现，条件探究性问题是本题的主要特征，我们可以通过特殊化思想进行求解，转换成联立方程组把首项求解出来，从而变成公比和公差问题，这样问题解决起来就会比较方便。

三、解题后反思要深入，思维创造性的培养

怎样通过数列解题教学把学生数学思维创造性培养起来？我们可以用常出错的问题来解答和教学，先安排学生自己解答探究问题，在批阅之后，老师把出现错误的问题汇聚起来，然后再把错解公布出来，让学生对错误解答进行反思，把错误的原因找出来，并且进行修改。案例分析：我们以以下题目为例进行探究。

①、{an}为等比数列，其中，a2a4a6a8的值为25。求出aaa9的值。

②、在数列{an}中，如果m2n-mm为an的值，求解改数列的前n项和。

在对学生作业批改中，老师发现有以下错误出现在了这个题目中：

错解：①、因为{an}是等比数列，对此得知：a4a6=aa8=aa9

通过已知条件a2a4a6a8=25，能够得到（a1a9）=25，所以，得出a1a9的值为±5.

②、推论得出：a1+a2+a3+......+an=Sn=

在教学中，通过有效的展示错题给学生，这样，对于错误的原因学生们我可以细心的琢磨，认真的分析。在①中，没有考虑等比数列内偶数项或者奇数项具有相同符号的这个隐藏条件，错解对公比是否唯1的讨论被遗漏，同时，还应该对有关数列是否是等比数列缺乏讨论。

在找到了错误的原因之后，学生们自己把错题改正过来就变得容易，而且，也加深了对这部分内容的理解和掌握。

结语：在过往的数学课堂教学中，我们总错误的理解为怎样教学学生解题就是解题教学，老师往往是合盘托出正确的解题过程，可以说，老师直接把“胜利的果实”呈现到学生面前让他们去品尝，即便学生当时能够明白这样解题的道理，但是，对于学生数学思维缺陷却无法被显示出来。相反，在解题中，让学生反思自己的错解，对于这种缺憾可以很好的进行弥补，此期间，学生的自我认识也将得到飞越。

参考文献

[1]陈华安.解题教学要引导学生学会如何思考——以一道递推数列求通项公式测试题的教学为例[J].数学教学研究，2012（7）：31-34.

[2]林凤.高中数学解题教学中逻辑思维的培养——以数列解题为例[J]教学分析.2017（07）：765-766.

[3]徐爱勇.如何实现解题教学从“课本”向“高考”的跨越——从教材一道数列习题谈起[J].中学数学研究，2018（02）：985-986.