初中数学开放探究题的类型及解题策略

李同天

摘要：文章对初中数学开放题的类型与特点进行分析，并通过教学实例，重点阐述结论开放型习题的解题方法，主要包括由因导果、画图解法、大胆猜测等方式，使学生的发散思维与解题能力得到显著提升。最后，还提出了科学有效的教学策略，力求通过坚持教学开放、贴近实际生活、注重学生情绪等方式，在开放题教学中贯彻落实陶行知教育理念，使学生能够真正理解知识，并做到灵活运用。

关键词：初中数学 开放探究题 解题策略

在初中数学教学中，开放探究题属于重要题型之一，是指命题中缺少一定条件或未给出明确结论，需要学生通过猜想、推断、证明的问题。开放探究题具有内容丰富、形式多样、创新性强等特点，对学生的数学基础与解题能力具有较高要求。对此，教师应注重解题策略与技巧的传授，坚持开放式教学，贴合学生实际生活，帮助学生克服畏惧心理，掌握多种解题方法，又快又准地完成习题解答。

一、初中数学开放题概述

1.习题类型

开放探究题的类型多种多样，具有代表性的类型如下。一是条件开放。此种题目一般是根据所给的结论，反思应具备的条件，并且此类条件并不具备唯一性。例如，若AB与DB相等，∠1与∠2相等，请填写适当的条件，使△ABC与△DBE全等，则需要填写的条件应为（ ）。此类题目便是条件开放式习题。二是结论开放，在相关条件之下，对相应对象是否存在进行探究。其一般有两种结果，即结论存在或不存在。在解题时，需要先假设其存在，然后根据既定条件演绎推理，最后得出结论，并对结论是否存在进行判断。三是条件与结论均开放。此类习题的条件与结论均不固定，需要学生根据已知信息自行填写、推理和分析，对内部蕴含的结论与数学规律进行探索。例如，30名学生乘坐两辆汽车去学校，在与学校相距10km之处，一辆车子发生故障。此时还有40min上课，正常行驶的车辆的限客数量为20人，汽车行驶的速度为50km/h。问在此情况下，全体学生是否会迟到？在对这一问题进行分析时，重点在于在只有一辆车子的情况下，首批学生已经到校，剩余学生是在原地等待，还是步行一段路程。两种不同走法所得的结果也不尽相同。

2.习题特点

一是新颖性。此类题目条件较为复杂，最终结论不固定，且解题方式多种多样，没有固定的模式可套用，且与学生的日常生活贴近，可改善传统封闭式题目的简单化、机械化解题的弊端。

二是灵活性。此类题目较为生动灵活，部分题目可追溯出多种条件、探究出多种结论，解法不尽相同，充分体现数学自身的灵活性。

三是发散性。此类题目还具有较强的发散性特点。由于答案不一致，在解题时需要应用多种思维方式，从多角度着手进行观察、对比和分析，探究各类解题方向。

四是创新性。此类题目创新性强，在教育功能方面优势明显，符合当前数学领域的人才培养目标。

二、初中数学开放探究题的解题方法

在初中数学习题体系中，开放探究题的类型众多。本文以结论开放型为例，通过案例分析，对此类题型的解题方法进行探究和阐述。在解题过程中，应根据现有条件推测相应的结论，与条件相符的结论多种多样，具体的解题方法如下。

1.由因导果

此种解题方式是从题意分析着手，顺向推理，也可根据题目已知内容，通过观察、计算、归纳等方式，得出最终结论。

例：已知△ABC和△DEC均为等腰直角三角形，但两者的大小不尽相同。如若将AE和DB两条线连接，判断AE与DB的数量与位置关系，并说明理由（如下图1所示）。如若将DB连接起来，并将该直线以D为顶点顺时针旋转90°，转到DF线处，将AF连接起来，判断DE与AF线的数量与位置关系，并说明理由（如下图2所示）。

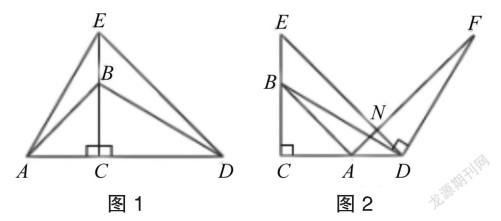
分析：首先对图形特点进行分析。根据已知条件AE与DB的位置选择相应的图形，并列出条件，根据Rt△ACE与Rt△BCD间的全等关系得出最终结果。在解答第二问时，可在第一问答案的基础上，对直线DE与AF的数量、位置关系进行探究。

解题：（1）直线AE与DB长度相等，且二者处于垂直状态。原因为：

根据图1可知，将直线DB延长，与AE相交于点M。因CA与CB相等，CE与CD相等，∠ACE与∠BCD均为90°，因此Rt△ACE与Rt△BCD具有全等关系，进而AE与DB相等，∠AEC与∠BDC相等。又因∠AEC与∠EAC相加为90°，在△AMD中，∠AMD的数值为90°，所以AE与DB为垂直状态。

（2）直线DE与AF长度相等，且二者处于垂直状态，原因为：

根据图2可知，假设ED与AF相交于点N，根据已知条件可知，直线BE与AD相等，由于∠EBD减去∠BDC等于90°，∠ADF减去∠BDC等于90°。因此∠EBD与∠ADF的数值相等。又因直线DB与DF相等，因此△EBD与△ADF之间为全等关系，因此DE与AF相等，∠FAD与∠E与∠EDC均为45°，进而∠AND为90°，也就是DE与AF之间为垂直关系。

评析：在对此类问题进行解答时，应按照已知条件进行猜想和证明。通常情况下，开放习题对学生的逻辑思维提出较高要求，对其归纳、推理能力进行考察。在判斷某个结论是否成立时，应根据情形进行分类讨论，灵活运用学过的定理与公式等知识，便可精准、高效地解决此类问题。

2.大胆猜测

在开放题教学中，教师应在陶行知教育思想的引导下，坚持“教学做合一”原则，通过开展小组合作探究的方式，使数学知识能够在实践中贯彻落实，激发学生的数学兴趣，培养其解题自信。此类开放题属于特殊的数学题目，其条件、答案与解答不尽相同。一些问题无法由一个学生在有限时间内完成，需要发挥集体的智慧。在解题过程中，对于全开放式结论，不妨通过大胆猜测的方式，猜想可能出现的各种结论，并对想到的结论逐一验证，直至得出与题目条件相符的答案。对此，在开放题解题中，教师可在陶行知“教学做合一”思想的引导下，通过小组合作学习等方式解题。根据合作学习理论，学生在小组中扮演不同角色，对每个人的工作进行分配，有助于独立、竞争与合作三种意识的锻炼和提升。在小组探究活动中，教师给出以下题目。

例：已知点P（x，y）位于第二象限，且y的数值不超过x+4，x与y均为整数，请写出一个与上述条件相符的坐标。

题目一出，各小组便纷纷展开讨论。根据已知可知，P点位于第二象限，那么x的数值小于0，y的值大于0，因此x>-4。又因x为整数，因此可猜测其数值可能为-1， -2，-3。若x的值为-1，则y的数值为1、2和3；若x的值为-2，则y的数值为1和2；若x的值为-3，则y的数值只有1。

在此过程中，教师发挥主导作用，组织好课堂纪律，并在恰当的时机引导学生，及时帮助小组走出困境。当小组讨论取得成果时，教师应及时表扬和鼓励。此类题目主要对学生基本概念的掌握情况进行考查，要求其具备发散思维，能够快速、精准地获取答案。在解答此类题目时，教师应引导学生从问题的角度出发，对已知条件中的关键性信息进行概括，再利用所学知识进行重建，通过猜想与拓展，形成新的知识体系，利用新知识中的内在联系解答问题。

三、初中数学开放题教学策略

1.坚持教学开放，控制开放度

在现代化教学背景下，传统的数学教学理念与方法难以满足现实需求，不利于新型人才培养。而开放题教学理念与模式能够做到与时俱进，满足当前的人才发展需求。对此，在实际教学中教师应坚持开放教学，也许在短期内难以看到明显效果，但长此以往，学生不但可积累丰富的知识与技能，发散思维也将得到有效锻炼和提升，数学学习兴趣更加浓厚。在学生发散创新思维的教学中，每位教师都应认识并尊重学生的个体差异，并根据差异性控制好课堂教学的开放度，要做到收放自如。

2.贴近实际生活，培养学生的应用能力

数学属于基础学科之一，是数量关系与空间图形的综合体。在数学学习中，大多数概念和理论均由数学家抽象概括而成，具有较强的抽象性，为学生学习带来一定难度。对此，在实际教学中，教师应尽量以实际生活为背景，与中学生的社会生活环境相贴合，营造民主、轻松的氛围，以此锻炼学生的发散思维。在正式教学之前，教师应恰当地选择题目，遵循陶行知“生活即教育”的原则，多设计一些与学科本身、生活实际相关的题目，拉近学生与数学间的距离，让其切实感受到生活处处有数学，同时也认识到学科之间的联系，并由此产生学习兴趣。同时，在教学要求方面，不应单纯为了完成教学目标而设计教学活动，而是要注重学生对理论知识的掌握与应用能力的提升。适当减少基础知识考查的题型，增加一些有层次、开放性的题型，这样便可在巩固基础知识的同时，促进学生思维能力、应用能力的提高。

3.注重学生情绪，克服畏惧心理

在以往的数学教学中，学生受传统教学模式影响，已经习惯了完整的已知条件与唯一的结论。因此，在思考与解答时，学生经常采用固定的思维模式，很难做到举一反三。在解答数学题时，要么轻松搞定，要么无从下手，这势必会对学生的解题自信造成打击，不利于思维锻炼。由于开放题具有较强的灵活性、开放性，传统的解题方式不再适用，难免会引起学生的情绪波动，甚至会影响学生的数学兴趣，使其厌倦、畏惧数学。对此，在开放题教学中，教师应奉行陶行知的教育思想，“捧着一颗心来，不带半根草去”，在传授理论知识的同时，注重每位学生的情绪与心理，及时给予鼓励和帮助，引导其朝着健康的方向发展。在教学过程中，还可建议学生写学习日记，及时了解学生的心理变化，帮助其树立数学自信，有效克服畏惧心理，显著提高数学成绩。

四、结语

综上所述，在新课改背景下，初中数学开放性习题已成为主要题型之一，对学生思维与数学品质的培养具有重要作用。对此，教师应深刻认识到此类题目的教育价值，并在各类题目的基础上对其内涵进行挖掘，探索更多科学有效的解题策略，通过坚持教学开放、貼近实际生活、注重学生情绪等方式，激发学生的思维与潜力，使其综合素质得到进一步提升。

参考文献

[1]王卓峰.谈初中数学开放题的类型与解题策略[ J].课程教育研究：新教师教学，2019（24）.

[2]赵娟.初中数学开放性习题的常规类型及其解题思路[ J].数理化学习：教育理论，2017（1）.

[3]李燕京.初中数学开放性习题的常见类型及其解题策略[ J].教育教学论坛，2019（30）：115-116.

[4]宋蓓.初中数学解题策略的研究及应用[D].天津师范大学，2019.