基于新课程背景下的数学习题教学研究——以“二次函数的最值问题”教学为例

◇ 甘肃 韩多瑞

二次函数是初中和高中数学课程里最重要的一种函数模型,它是提高学生思维与运算能力的一个载体,是高考和数学联赛试题的热点和难点.因此,有必要对二次函数的函数最值问题求解策略进行更深层次的探究.

1 最大(小)值定义

1)一般地,设函数y＝f(x)的定义域为I,如果存在实数M满足：

a)对于任意的x∈I,都有f(x)≤M；

b)存在x0∈I,使得f(x0)＝M.

那么,我们称M是函数f(x)的最大值,记作

2)一般地,设函数y＝f(x)的定义域为I,如果存在实数m满足：

a)对于任意的x∈I,都有f(x)≥m；

b)存在x0∈I,使得f(x0)＝m.

那么,我们称m是函数f(x)的最小值,记作

2 二次函数的最值问题解法分析

2.1 利用函数单调性定义求最值问题

所谓的函数单调性也可以称为函数的增减性,也就是当函数f(x)的自变量在其定义区间内增大(或减小)时,函数值f(x)随着自变量而增大(或减小),则称该函数为在该区间上具有单调性.

分析在解这种问题时,我们可以采用函数单调性的定义来解决,即增函数与减函数定义：对于函数f(x)的定义域I内某个区间上的任意两个自变量的值x1,x2.若当x1＜x2时,都有f(x1)＜f(x2),则f(x)在这个区间上是增函数；若当x1＜x2时,都有f(x1)＞f(x2),则说f(x)在这个区间上是减函数.

通过让学生回忆定义并提问的方式,进行课程第一步,然后逐步引导学生进行计算.

解设2≤x1≤x2≤6,有f(x1)－f(x2)＝(x1－x2)(x1＋x2).

因为2≤x1≤x2≤6,所以x1－x2＜0,则f(x1)－f(x2)＜0,所以f(x1)＜f(x2),所以函数y＝x2－1在该区间为增函数.所以当x＝2时,函数y＝x2－1取得最小值为3；当x＝6时,函数y＝x2－1取得最大值为35.

2.2 用函数图象数形结合解题

分析像这类考查图象和单调性的问题,我们可以先将其函数图象画出来,根据图象判断出函数的单调区间,再用定义法加以证明.而这种方法常常适合于选择题和填空题.

解根据题目画出函数图象,因y＝－x2＋2|x|－3＝所以函数图象如图1.

图1

由图象可得,函数在区间(－∞,－1)和(0,1)上单调递增,在区间(－1,0)和(1,＋∞)上单调递减,最高点是(±1,－2),因此函数在(－∞,－1),(0,1)上是增函数,在(－1,0),(1,＋∞)上是减函数,最大值为－2.

2.3 复合函数单调性判别法

分析这是一道典型的复合函数单调性的求解问题,在进行复合函数的单调性求解时需要根据复合函数的定义,即对于函数y＝f(u)和u＝g(x),如果u＝g(x)在区间(a,b)上具有单调性,当x∈(a,b)时,u∈(m,n),且y＝f(u)在区间(m,n)上也具有单调性,则复合函数y＝f(g(x))在区间(a,b)具有的单调性,规律如表1.

表1

当两个函数的单调性相同时,其复合函数是增函数；当两个函数的单调性不相同时,其复合函数是减函数.

解先确定定义域：x2＋2x－3≥0,得到x≤－3或x≥1,所以函数的定义域为

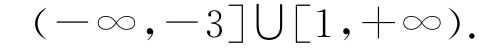
令u＝x2＋2x－3,则；因为在[0,＋∞)为增函数,而u＝x2＋2x－3在(－∞,－3)为减函数,在(1,＋∞)为增函数,所以函数y ＝的单调递增区间为(1,＋∞),单调递减区间为(－∞,－3).

在解复合函数问题时,先判断函数的定义域,然后对复合函数进行拆解.

2.4 导数判别法

根据导函数的定义：如果函数y＝f(x)在x 的某个开区间内,总有f′(x)＞0,则f(x)在这个区间上为严格增函数；如果函数y＝f(x)在x 的某个开区间内,总有f′(x)＜0,则f(x)在这个区间上为严格减函数.

在用导数判别法进行函数单调性的计算时,还需要注意f′(x)＞0是f(x)为增函数的充分不必要条件,f′(x)＜0 是f(x)为减函数的充分不必要条件.如f(x)＝x3在R上为增函数,而f′(0)＝0,所以在x＝0处不满足f′(x)＞0.故有可导函数f(x)在某个区间内单调递增(或递减)的充要条件为f′(x)≥0(或f′(x)≤0)(f′(x)不恒为零).

二次函数是高中阶段的重点,而函数的单调性又是二次函数的重要部分,所以我们一定要把握好重点,才能用导数来准确判断函数的单调性.

要求a 则必须消去参数b,c,从而

在这里涉及了导数求最值的一个重要方法,它可以便于学生解决二次函数的求最值问题,即切比雪夫多项式.它的两个性质如下.

性质1设二次函数f(x)＝ax2＋bx＋c,若对任意的x∈[－1,1],|f(x)|≤1,则|a|max＝2.

性质2对于任意二次项系数为1 的二次函数f(x)必有,当且仅当f(x)＝x2－时,等号成立.所以,在遇到上述的题型时,我们可以直接求其导数,然后求f′(1),f′(),f′(0)即可.

用导数法求函数的单调性及单调区间可以分为以下几个步骤.

1)确定定义域；

2)求f′(x)；

3)在f(x)的定义域内解不等式f′(x)＞0 和f′(x)＜0；

4)确定函数f(x)的单调区间.

需要注意的是单调区间不以“并集”的形式出现.

3 结语

通过上述相关例题与解析,我们能清晰地找到解决这类二次函数问题的方法.教师的任务就是针对某些问题多研究与反思,尝试用不同的角度以及数学解题方法揭示问题背后的本质.“授人以鱼不如授人以渔”,让学生从本源上理解问题,学生解决这类问题才能如鱼得水,游刃有余.