考虑应力分布约束的压电全向加速度计梁结构优化设计

王 岩，赵 剑，夏 阳，刘蓬勃

(大连理工大学 工业装备分析国家重点实验室 汽车工程学院，辽宁 大连 116081)

1 引 言

全向、多轴及多个单轴加速度计可以实现加速度信息的全向敏感，广泛应用于各类运载工具、人体的惯量信息采集[1-5]。与单轴加速度计相比，全向或多轴加速度计可以大量减少惯性单元数量，降低多惯性器件的累计误差、布放及线路成本。

弹性梁是目前加速度计常用的结构形式[6-12,22-24]，通过设计不同形式的细长梁结构，利用功能敏感材料来测量其局部应力、应变或由应变产生的位移，实现对加速度的敏感。例如，压电或压阻加速度计，将压电或压阻片贴于悬臂梁或正交悬臂梁端部附近，实现单轴或多轴加速度敏感[6,11,13]。电容加速度计采用“之”字形细长梁或细长平行梁，利用径向受力易产生应变的特性实现单轴或多轴高灵敏度[12,14-15]。然而，该高灵敏结构通常在梁端部附近会产生应力集中现象。如果弹性梁结构设计不合理，易在截面或者曲率突变部位出现因应力集中而导致的破坏现象，从而降低传感器的可靠性、抗冲击性。另外，由于局部应力过大，也会制约器件的最大线性测量范围(量程)。

然而，若仅采取措施降低梁式加速度计结构局部应力集中的问题，也会同时影响器件灵敏度。例如，常用的加粗悬臂梁端部方法，虽然可以降低其应力集中，但传感器的灵敏度也会下降。鲜有直接改变加速度计梁结构形式以降低其应力的报道。另外，高g值压阻加速度计采用间接方法降低梁结构应力[16-20]，即采用大尺度的支撑梁与细长压阻梁组合结构。通过粗大支撑梁来支撑惯性质量块并减小细长敏感梁的应变，以避免其应力过大而失效。该方法借助细小梁状压阻器与支撑梁共存结构以平衡梁结构应力分布与灵敏度之间的制约关系，提升了结构抗冲击性。但粗大的支撑梁限制了器件灵敏度的提升。而对于非高g值的梁结构加速度计，仍缺少有效提升灵敏度并降低梁应力的设计方法。因此，提高灵敏度并降低梁结构应力集中现象是梁式加速度计存在的设计难题。

本文以压电加速度计高灵敏度为目标，建立了考虑应力分布状态的新型全向加速度计柔性支撑结构(压电梁)优化设计模型。通过协同优化初始长度为15 .0 mm的压电梁不同部位的曲率和直径，设计了具有变截面特征的压电曲梁全向加速度计。优化后的曲梁加速度计全向灵敏度较初始直梁加速度计显著提升，其最大应力低于初始直梁加速度计，有效验证了所提出的灵敏度与应力分布协同优化方法的有效性。

2 压电梁应变-电荷转化关系

构型和极化方向是影响压电梁传感器敏感性能的关键因素。通过描述空间轴向极化梁的应变-电荷转化关系有助于说明构型影响敏感性能的机理。

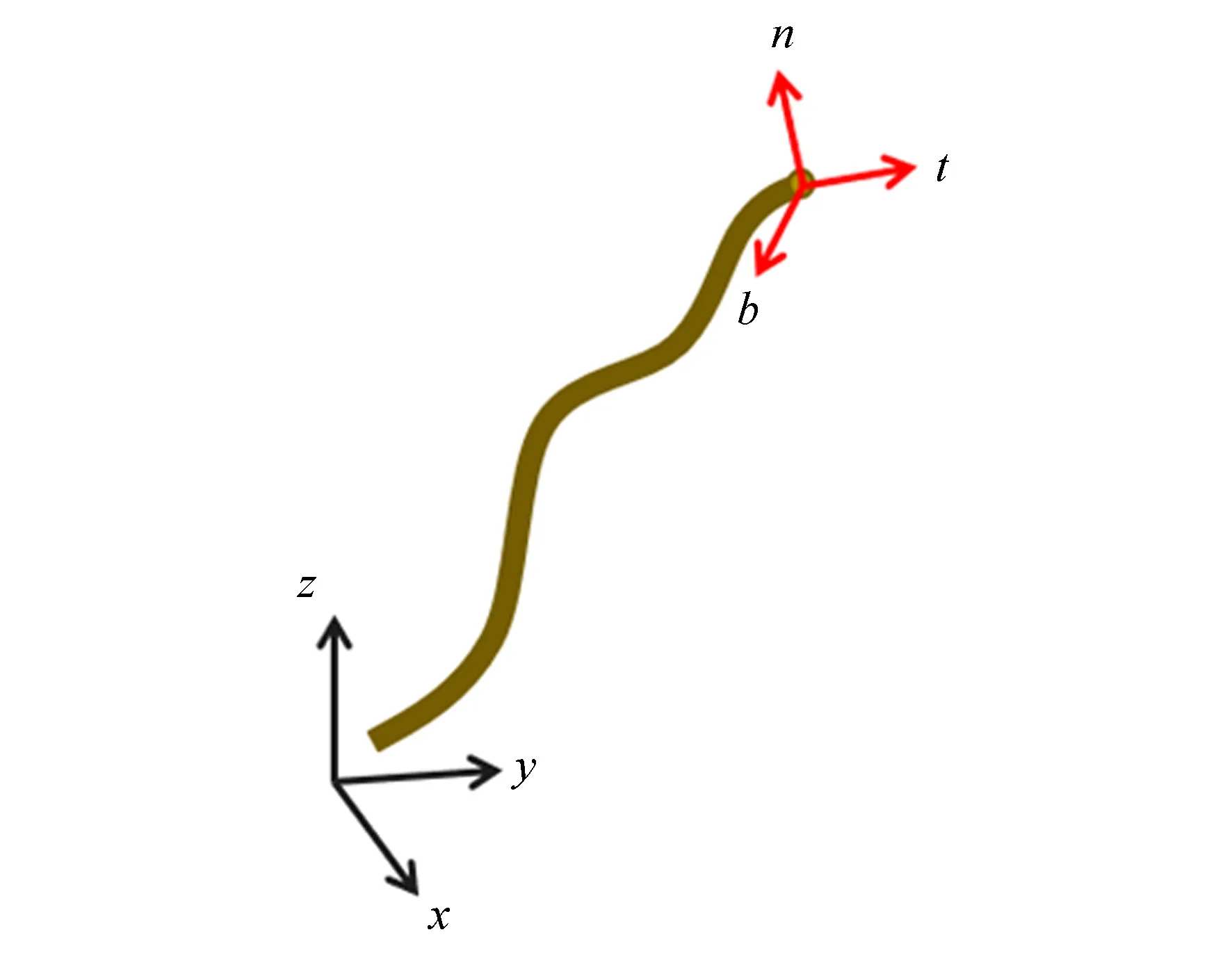
图1 梁结构坐标系Fig.1 Beam structure coordinate systems

图1通过分别定义全局坐标系x-y-z和局部坐标系t-n-b描述一个典型的空间梁结构。控制方程在局部坐标系中进行定义。位移矢量u和旋转矢量θ用于描述梁的运动学状态。式(1)用于描述广义位移ε(轴向和剪切)应变和广义旋转χ(扭转和弯曲)应变。

ε=u′-θ×t

χ=θ′，

(1)

其中：′表示对弧长求导，t表示梁的单位切向矢量(不表示时间)。在线弹性本构方程(2)中，N和M分别表示广义内力和力矩。

N=Cε,M=Qχ,

(2)

其中：C=[EA，GA1，GA2],Q=[GJ，EI1，EI2]，均为材料矩阵。

梁平衡状态表示为：

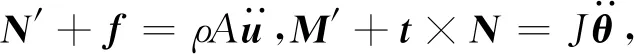
(3)

3-方向表示轴向方向，在图1局部坐标系中用t-方向表示。当压电梁极化和产生的电场都在3-方向时，可采用式(4)描述其线性本构关系[21]：

(4)

当压电梁被用作传感器时，由外载荷产生的E3为极小值量，在式(4)中认为是零。式(5)表示压电梁微段Δs两端的电势差：

(5)

其中：Q为微段Δs两端的电荷，ΔC为微段Δs两端的电容，A为截面面积，μ为泊松比。式(5)描述了U和ε3的转化关系，可知电势差与轴向应变成正比。式(6)描述了压电梁两端的电势差：

(6)

3 压电梁全向加速度计初始构型

3. 1 初始构型

论文采用ANSYS中的Beam189梁单元(铁木辛柯梁)对加速度计中的梁结构进行建模，采用实体单元对加速度计中的质量块建模，采用谐响应分析计算加速度计在加速度载荷下的应力应变。采用COMSOL Multiphysics软件计算由梁应变产生的电压。

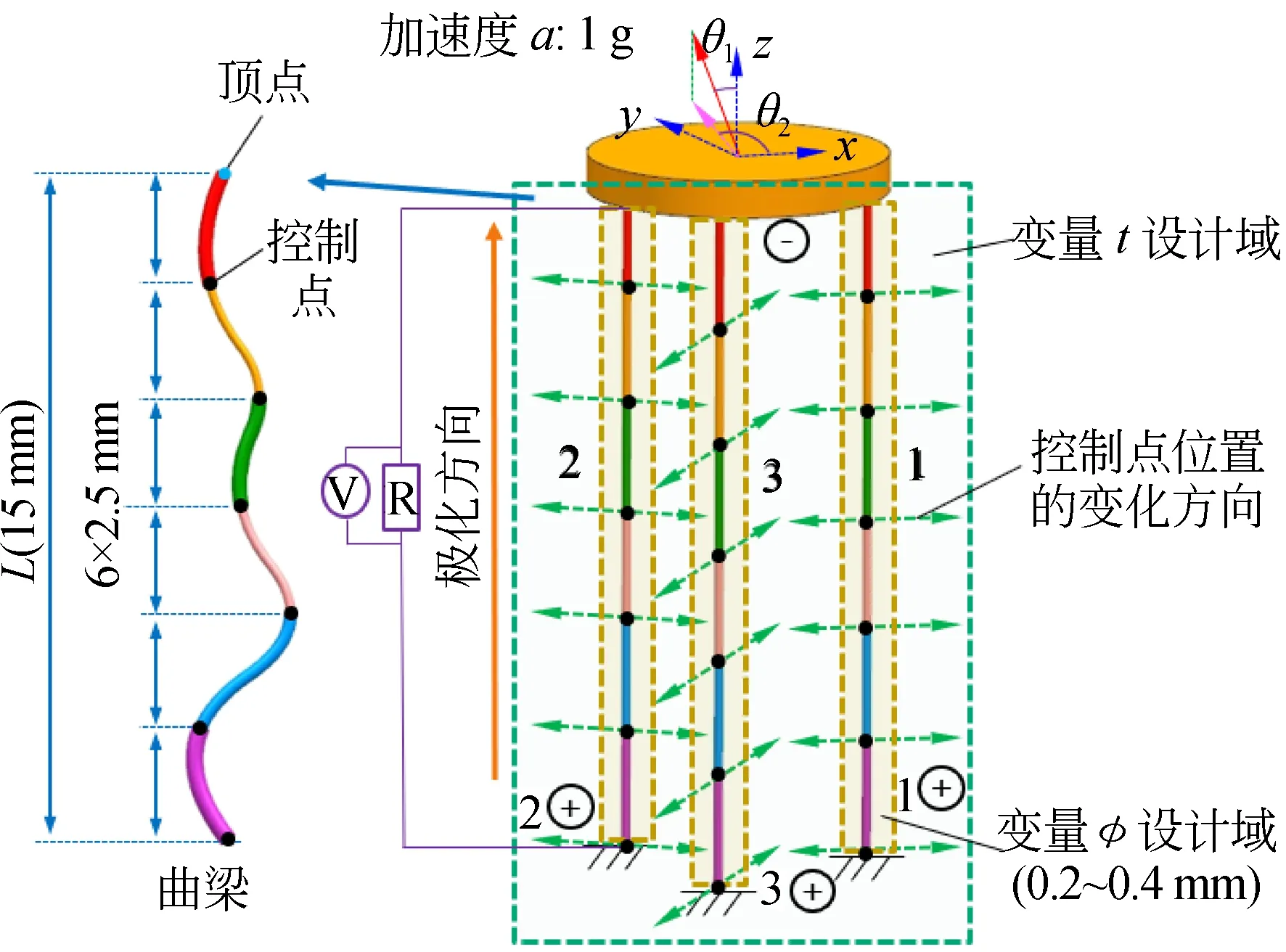
图2 初始压电直梁加速度计及优化模型Fig.2 Initial piezoelectric straight-beam accelerometer and optimization model

3.2 全向加速度计解算方法

根据第2节结论：轴向极化的压电梁输出电压与轴向应变成正比，本节建立了全向加速度计解算方法。表3中U1x,U2x,U3x,U1y,U2y,U3y,U1z,U2z,U3z分别为加速度计在x,y,z轴方向，相同大小加速度下梁1，2，3输出电压和轴向应变比例。

因为U1y为极小值，令U1y=0。根据以下规律：U1x+U2x+U3x=U1y+U2y+U3y=0，U1z=U2z=U3z，可以得到解算3D加速度方向和大小的计算方法，该方法适用于初始和优化加速度计。

假设U1,U2,U3为在3D加速度下梁1，2，3的输出电压或轴向应变。Ux,Uy,Uz分别为输出电压或轴向应变矢量在x,y,z轴的分量。

由3D加速度产生的电压或轴向应变矢量在x,y,z轴的分量比例为：

(7)

其中：β是一个系数，初始加速度计中β=1。当三梁的构型和直径都改变，β的数值通常会发生改变。

式(8)反映3D加速度产生的电压或轴向应变矢量的大小(全向灵敏度Sc)：

(8)

4 高灵敏低应力构型优化

以初始直梁加速度计作为初始构型，以梁不同部位的曲率和直径作为设计变量，借助遗传算法，优化设计得到了具有到高灵敏低应力特性的加速度计梁构型。由式(6)可知，轴向极化压电梁的输出电压与轴向应变成正比，优化中将轴向应变作为优化目标，压电梁最大应力作为约束条件。在优化中采用ANSYS进行谐响应分析计算50 Hz的3D加速度下梁的应力应变，并借助COMSOL计算由应变产生的输出电压。

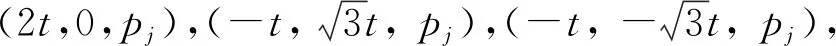
(9)

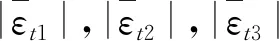
|χmaxEr|为三梁最大弯曲应力绝对值，χmax为三梁全部单元中最大弯曲应变，E为弹性模量，r为梁截面半径。α为设定的应力上限。目标函数是为了找到在三梁最大应力约束条件下，具有最大轴向应变灵敏度的优化构型。变量1：t为6个控制点的x，y坐标参数，用于改变控制点的位移建立新构型。变量2：φ为梁6个部分的直径，每一部分均独立变化。图2中三梁高度相同(颜色相同)的部分直径相同(彩图见期刊电子版)。变量1和2总共12个变量数目。pj为三梁6个控制点的纵坐标，取值依次为0.0, 2.5, 5.0, 7.5, 10.0及12.5。

(10)

图2中采用θ1和θ2描述3D加速度的方向。θ1为俯仰角，即z轴正方向与加速度矢量的夹角；θ2为方位角，即x轴正方向与加速度在面内投影的夹角。θ1的数值周期为[0°, 180°]。由于三梁关于构型中心轴对称，所以θ2数值周期为[0°, 120°]。θ1和θ2的取值如图4所示。为了将周期[0°, 120°]12等分，θ2的取值为0°～110°，为了将周期[0°, 180°]近似12等分，θ2的取值为15°～178°。

表1 MATLAB中遗传算法关键参数取值

基于遗传算法优化中的关键参数列于表1和表2。为了使优化结果在3D加速度下具有普适性，优化中采用了如下3个α值及其对应的3D加速度方向：3.40(θ1=105°，θ2=60°)，3.50(θ1=60°，θ2=30°)，2.30(θ1=150°，θ2=90°)，如表2和图4所示。

将通过式(9)得到的优化曲梁加速度计轴向极化，如图3所示。在3种不同方向的加速度下得到的优化构型相同，这在一定程度上说明优化加速度计对3D加速度具有普适性。

表2 优化模型参数数值

表3 初始梁和优化梁加速度计在x，y，z轴载荷下三梁输出电压和轴向应变比例

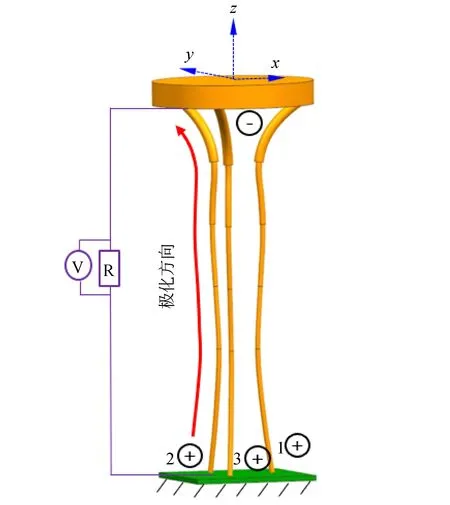
图3 优化曲梁加速度计Fig.3 Optimized curved-beam accelerometer

5 性能对比

5.1 输出电压和轴向应变解算比例

由于优化加速度计构型发生变化，与直梁支撑加速度计相比，其输出电压和轴向应变比例也发生了变化。由表3可知，在x，y轴方向，优化加速度计输出电压较初始加速度计提升了2倍以上；在z方向，优化加速度计输出电压有所降低。由于曲率和直径的变化，对于优化加速度计，式(7)和式(8)中β=0.4。

5.2 全向灵敏度与最大应力

为了表征加速度计的全向敏感及应力变化特性，施加了12种不同方向，1 g大小50 Hz的3D加速度。图4为两加速度计各梁在12种不同方向加速度下的电压绝对值(下文简称电压)曲线。优化加速度计三梁电压曲线变化趋势与初始加速度计基本一致，这是由于优化和初始加速度计的3梁均关于器件结构中心轴对称所致。在大多数各个方向的3D加速度下优化加速度计三梁电压在1.0～8.0 V内，均显著高于初始加速度计，大约为其1.5～3.0倍。而优化加速度计部分梁在个别载荷下的输出电压低于初始加速度计，如梁1在载荷10，11，12下，梁2在载荷4下，梁3在载荷12下的输出电压。由表5和表6可知，即使优化加速度计部分梁电压略低于初始加速度计，但由于其他梁的高电压输出，经过解算后的全向灵敏度依然保持不变。可见部分梁输出电压降低不会影响优化加速度计的全向灵敏度一致性。另外，两加速度计3梁的电压最大值分别位于不同载荷，这是由于3梁关于器件中心轴对称的结构布局在不同的俯仰角θ1、方位角θ2加速度下呈现出的特定电压数值规律。12种载荷下优化和初始加速度计三梁输出电压见表5。两加速度计通过三梁电压解算的电压矢量方向和大小见表6。可知两加速度计对3D加速度的大小和方向均具有良好的解算精度，且都具有良好的全向灵敏度一致性。优化加速度计全向灵敏度Sc为0.8 V/g，为初始加速度计的2.5倍。

优化加速度计同时实现了对全向加速度的低应力响应，如图5所示。除在载荷12下，优化加速度计最大应力略高于初始加速度计，其他11种载荷下，优化加速度计最大应力均低于初始加速度计。在其中9种载荷下，优化加速度计最大应力为初始加速度计的70%～90%。且优化加速度计最大应力只位于其中一根梁，而初始加速度计三根梁具有相同的最大应力。由于较低的最大应力且该应力只位于单根梁，优化加速度计结构可靠性显著高于初始加速度计。12种载荷下两加速度计最大应力数值见表5。

通过同时改变三梁不同部位的曲率和直径，优化压电曲梁的轴向应变和弯曲应力的分布，协同设计了梁结构轴向应变和弯曲应力对3D加速度的不同响应特性。通过高轴向应变响应(即电压输出)，优化加速度计实现了对3D加速度的高探测灵敏度；通过低弯曲应力响应，降低了优化加速度计梁最大应力，且该应力只位于单根梁。利用轴向极化的压电梁轴向应变与输出电压成正比的特定关系和特定的变截面曲梁构型，优化加速度计实现了梁结构加速度计的高灵敏、低应力设计。同时优化压电梁不同部位的曲率与截面直径，是得到高灵敏低应力构型的关键。其中优化曲率和截面直径对提高灵敏度都有作用；而优化截面直径对降低应力起主要作用。该设计解决了传统梁结构加速度计通过直接改变梁结构形式无法实现高灵敏、低应力响应的问题。

表4 前四阶固有频率

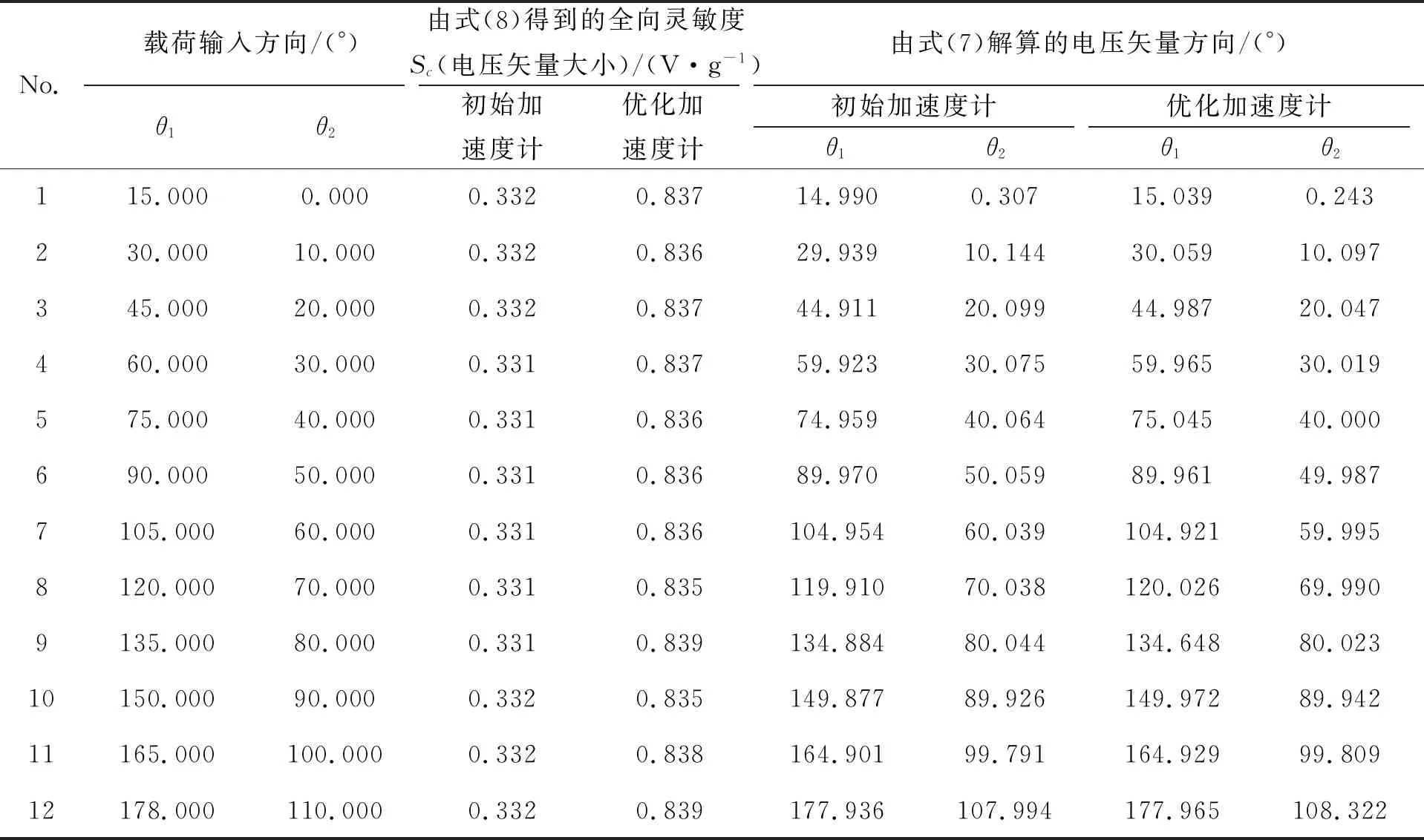
表5 在12种不同方向大小为1 g的50 Hz加速度下解算得到的电压矢量大小及方向

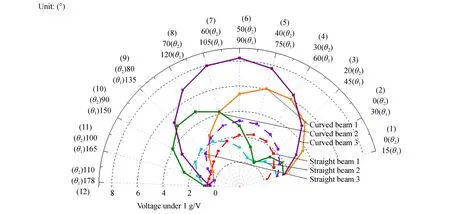
图4 在12种不同方向50 Hz的3D加速度下3梁电压Fig.4 Voltages of three beams under 12 various directional 3D accelerations in 50 Hz

图5 12种不同方向1 g大小50 Hz的3D加速度下最大应力Fig.5 The maximum stresses of three beams under 12 various directional 1g 3D accelerations in 50 Hz

5.3 全向分辨率

施加与图4中相同的加速度载荷，当θ1与θ2均增大10′时，通过三梁电压变化量大小反映两加速度计角度分辨率情况，如图6所示。可知优化加速度计在各个方向载荷下的三梁电压增量均高于初始加速度计，其均值为15.3 mV，为初始加速度计的3.1倍。这说明优化加速度计较初始加速度计具有更好的角度分辨率，可以更好的辨识3D加速度微小的方向变化。这是由于优化加速度计的全向灵敏度高于初始加速度计所致。

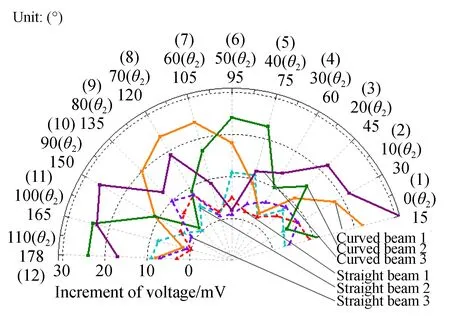
图6 角度分辨率对比图Fig.8 Angular resolution

5.4 低频段灵敏度

表4中为两加速度计前四阶固有频率。两者前二阶频率较低，适用于低频测量。图7为在图4中12种方向的加速度下，1～81 Hz频段内由式(8)得到的两加速度计全向灵敏度谐响应分析曲线。优化加速度计全向灵敏度Sc为0.7～1.3 V/g，为初始加速度计的1.6～2.9倍。由于受到1阶固有频率影响，优化加速度计测量频段被限制在低频段。

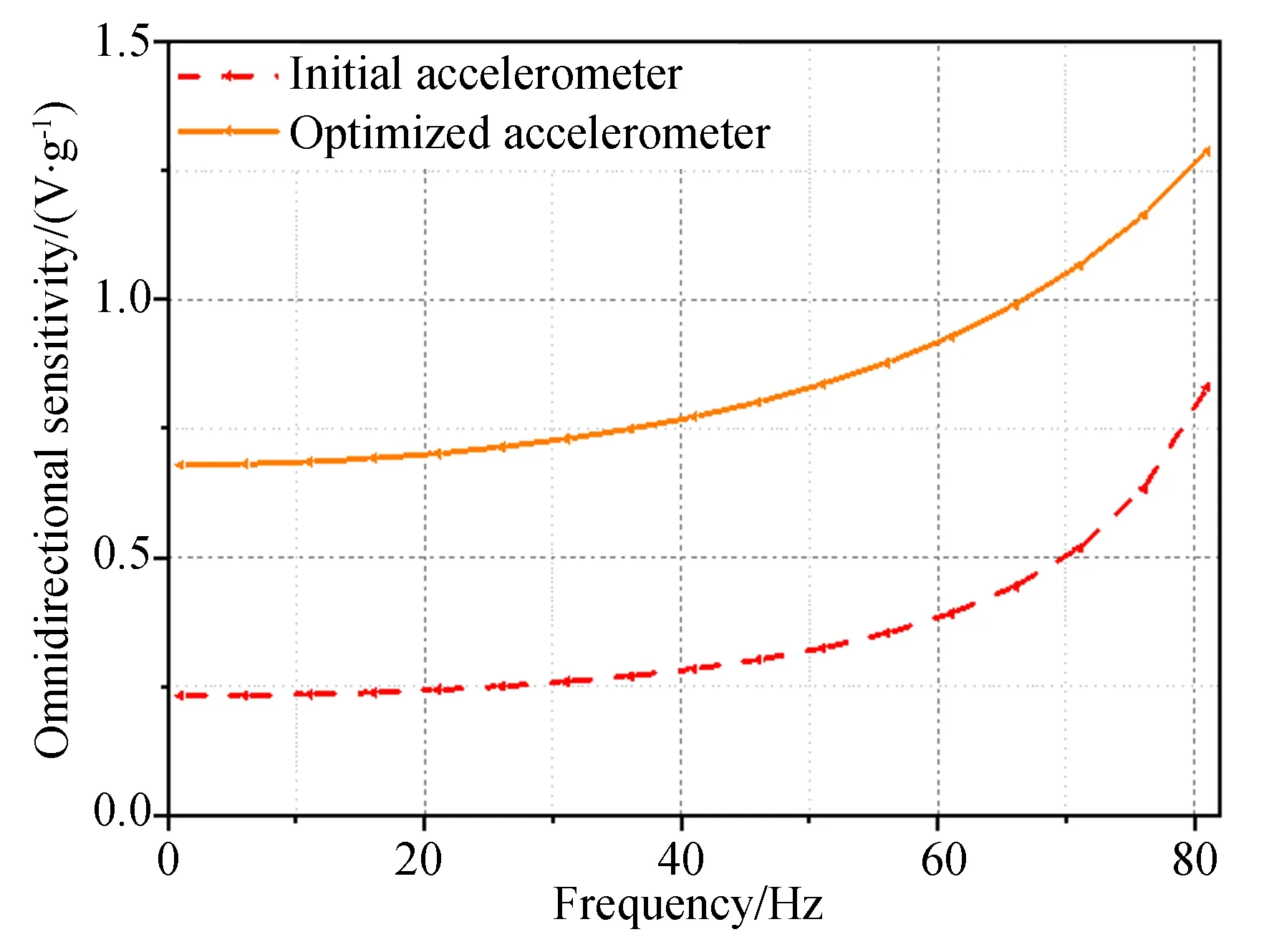
图7 1～81 Hz频段内全向灵敏度扫频曲线Fig.7 Omnidirectional sensitivity sweep frequency curve

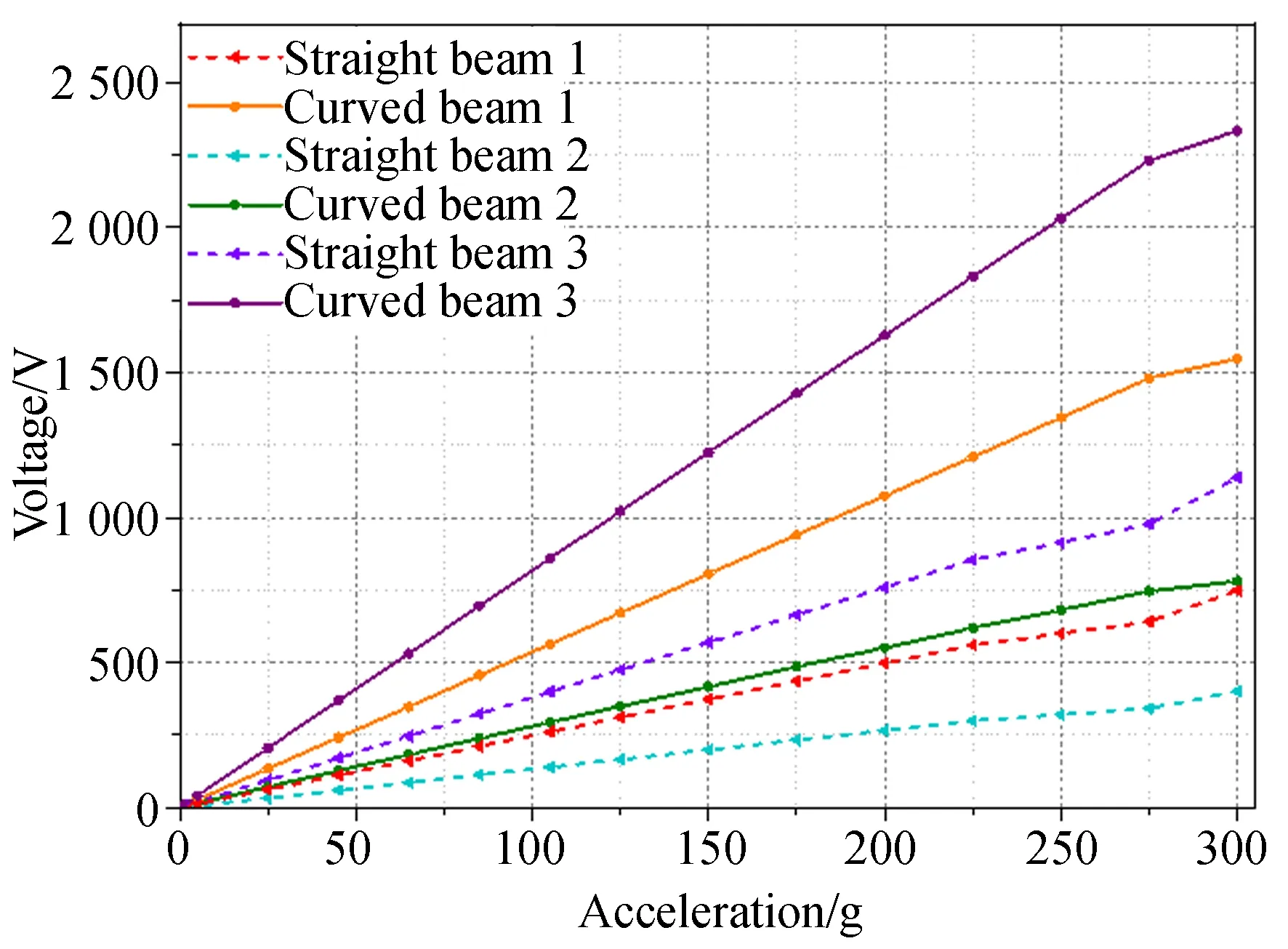
图8 加速度线性测量范围Fig.8 Linear measurement range

5.5 线性测量范围

图8为两加速度计在方向θ1=90°，θ2=50°(载荷6)50 Hz加速度下的加速度线性测量范围曲线。考虑实际测量系统的背景噪声和信号损耗，测量下限设定为0.1 g。初始加速度计的线性测量范围为0.1～225 g，在250 g以上区域出现非线性。优化加速度在该载荷下的线性测量范围为0.1～275 g，在300 g出现了非线性。因此，其最大线性测量范围为初始加速度计的1.2倍。由图7可知，载荷6下优化加速度计最大应力略低于初始加速度计，故在该载荷下优化加速度计在线弹性变形范围内可以响应更大的加速度。优化加速度计的低应力特性使其在达到材料屈服极限时可承受更大的加速度，故增大了其加速度线性测量范围。

6 结 论

针对全向加速度计柔性支撑结构应力集中问题，建立了考虑应力分布状态的新型全向加速度计结构优化设计模型。通过协同优化压电支撑梁不同部位的曲率和直径，设计了在3D加速度下具有高轴向应变(灵敏度)和低弯曲应力(最大应力)特性的压电曲梁，得到了优化压电变截面曲梁低频全向加速度计。其全向灵敏度为初始直梁等截面加速度计的2.5倍，其最大应力为初始直梁加速度计的0.7～0.9倍，且在1～81 Hz频段内体现出高灵敏度特性。该加速度计的设计解决了通过直接改变梁结构形式难以实现传统梁结构加速度计高灵敏低应力响应的问题。

由于高灵敏特性，优化曲梁加速度计角度分辨率显著高于初始直梁加速度计。由于低应力特性，优化曲梁加速度计的加速度线性测量范围为初始直梁加速度计1.2倍。优化曲梁加速度计对3D加速度的高敏感性能及低应力特性为高性能曲梁加速度计设计提供了借鉴。未来将对器件的制备、测试等问题进行研究。