结合改进Retinex及自适应分数阶微分的雾霾公路交通图像增强

王卫星，赵 恒

(长安大学 信息工程学院，陕西 西安 710064)

1 引 言

在雾霾天气情况下，图像由于大气散射作用被严重降质，使目标反射的光线发生衰减，从而造成道路交通图像存在着视觉效果差、对比度低、能见度弱及细节模糊等问题，给后续的图像处理工作如特征提取、目标追踪与识别带来了严峻地挑战[1]。因此，对雾霾天气条件下所获取的公路交通图像进行增强处理，提高清晰度、对比度及视觉效果是近年人们关注的热点，同时具有重要的理论研究意义和应用价值。

目前低质量的雾霾图像增强算法有多种：如简单的直方图均衡化的方法；基于大气物理模型的方法(如暗通道先验算法)，基于Retinex理论的方法等。直方图均衡化的方法[2-4]可以较好地提升图像的亮度和对比度。但是，由于灰度级合并易造成图像细节丢失，而且对于较为突出的图像信息会产生过度增强，不利于雾霾图像的色彩饱和度和对比度的改善。基于大气物理模型的方法是通过研究大气飘浮颗粒对光线的作用，建立大气散射模型[5-6]，利用图像退化的原理复原出降质前的图像。2011年，He等[7]提出了基于暗通道先验(Dark Channel Prior,DCP)的去雾算法，该算法去雾效果较好，颜色较逼真，但实时性差且去雾后的图像边缘处存在伪影等干扰信息。2013年，He等[8]提出一种局部线性滤波器即引导滤波器，其具有良好的边缘保持性能，可以用于优化透射率图，从而改善去雾效果。基于Retinex理论的方法是目前比较流行的图像增强算法。1971年，Land等[9]提出色彩恒常性理论即Retinex，指出人眼对物体色彩的感知取决于物体表面的反射特性，而与入射光强度无关。1997年，Jobson等提出单尺度Retinex (Single Scale Retinex，SSR)算法[10]和多尺度Retinex(Multi-scale Retinex，MSR)算法[11]，这两种算法都是用高斯平滑滤波估计原图像的照射分量，增强后的结果往往会有较严重的光晕产生。Elade[12]提出了基于双边滤波的Retinex算法，改进了以高斯函数为中心环绕函数的SSR和MSR算法，该算法在保持边缘和克服光晕上表现较好，但计算复杂度高，实时性较差。Ahn等[13]用引导滤波代替高斯滤波来估计亮度分量，提出ALTM (Adaptive local tone mapping based on retinex for high dynamic range images)算法，效率高并且能较好地保持边缘信息。基于引导滤波的方法在原始图像比较复杂且含有大量噪声时，在增强后的图像中噪声也会增强。因此，Li等[14]提出了一种加权引导滤波，以自适应因子为权重来抑制噪声，提高保边平滑的性能，但去噪效果不明显，细节对比度不高。基于Retinex理论的图像增强方法的关键在于对原图像照射分量的估计，然而在反射分量未知的情况下对照射分量的估计是不准确的。另外，因为分数阶微分在增强图像弱信息方面有良好表现，使得其成为图像细节增强研究中被广泛使用的方法。Hu等[15]提出了非整数步长来提高复杂环境下分数阶微分的增强性能。也有人提出使用改进的Ostu方法将图像分割，然后根据其区域特征建立自适应分数阶微分算子[16]。

鉴于以上分析，本文在现有研究的基础上，提出了一种基于快速引导滤波平滑约束的Retinex方法来获取初始反射分量，并使用自适应分数阶微分对获得的反射分量进行增强，以提高图像的对比度和清晰度。对于采集到的低质量雾霾交通图像，利用该方法与近几年国内外主要的雾霾图像增强方法进行处理，并从主观性能和客观评价方面进行了比较分析。

2 算法设计思路与原理

2.1 Retinex理论模型

色彩恒常性理论即Retinex理论是由Land等[9]在1971年提出的，其基本思想是入射光决定图像中各像素点的动态范围而物体的颜色是由其表面的反射属性来决定的，属于固有属性和光照情况无关，其基本模型可表示为：

S(x,y)=R(x,y)×L(x,y),

(1)

其中：S(x,y)为输入的待增强图像；L(x,y)为光照图像分量即照射分量；R(x,y)表示反射图像分量。通常，将一副图像分为照射分量L(x,y)和反射分量R(x,y)两部分，通过降低或去除照射分量对反射分量的影响，就可以得到图像的本质视觉效果，从而达到图像增强的目的，如图1所示。因此，如何准确估计照射分量对图像增强的效果至关重要，也是Retinex算法的关键步骤。为了方便计算，常常通过对数变换将乘法运算转换为加法运算。

2.2 色彩空间转换模型

对于彩色图像，由于R，G，B 3个空间通道之间独立性低，若对各个通道分别进行增强再叠加往往会出现颜色失真的现象，因此本文将待增强图像从RGB转换为YCbCr颜色空间，利用亮度分量构建初始图像I′(x,y)，经过算法处理得到增强后的Y分量，将其与Cb，Cr分量重新合并，最后再将上述结果从YCbCr转化为RGB颜色空间，以避免结果图像出现颜色失真现象。

YCbCr颜色空间是一种基本的色彩空间模型，其中分量Y表示亮度，Cb和Cr指色度分量，用来描述图像色彩和饱和度属性。RGB与YCbCr颜色空间之间可以相互转化，映射关系如式(2)所示：

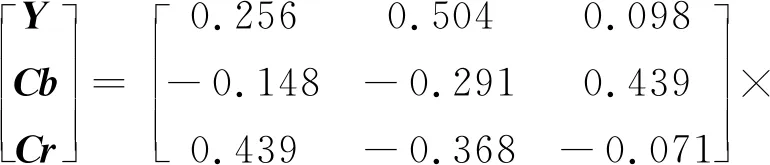
(2)

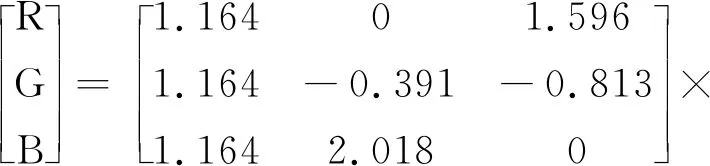
(3)

2.3 照射分量估计

Retinex算法是目前最为常见的图像增强方法之一，根据具体应用场景的不同产生了很多改进算法如：MSR，MSRCR，以及多种方法结合的Retinex算法等，总的来说，改进的算法很多都是围绕如何正确估计照射分量而展开的。

一般来说，Retinex理论假设照射分量分段光滑，但从待增强的图像S(x,y)中求取照射分量L(x,y)是一个病态问题，因此在增强的图像中容易出现光晕现象。为了尽量避免照射分量的影响，通常在求解照射分量时会增加约束项使其分段光滑。2003年，Kimmel等将Retinex模型的照射分量的估计转化为二次规划问题进行求解，并引入变分模型以能量泛函数的形式表达Retinex理论，其中变分模型是一种处理函数的数学方法，可以求得使泛函数取得极大值或极小值的极值函数[17]。经典的目标函数表示如式(4)所示：

(4)

式中：λ为加权系数；S为输入图像；Dx和Dy分别代表水平方向和垂直方向的梯度算子，目的是使照射分量L分段光滑。

通常，求解此问题常用到的有基于全变分的方法[18]，其通过使用1范数平滑约束来替代式(4)的2范数平滑约束，通过多次迭代来获得近似最优解，求解过程比较耗时。Elade提出了基于两个双边滤波器的Retinex图像增强算法[12]，在式(4)照射分量L(x,y)的估计中增加空间平滑性约束条件来校正计算结果，即将双边滤波作为一种空间平滑约束条件，添加到照射分量的估计中来，这样可以得到一种非迭代的Retinex算法，该算法可以更好地处理照射分量的边缘信息，避免出现光晕现象，也可以抑制暗区中的噪声。

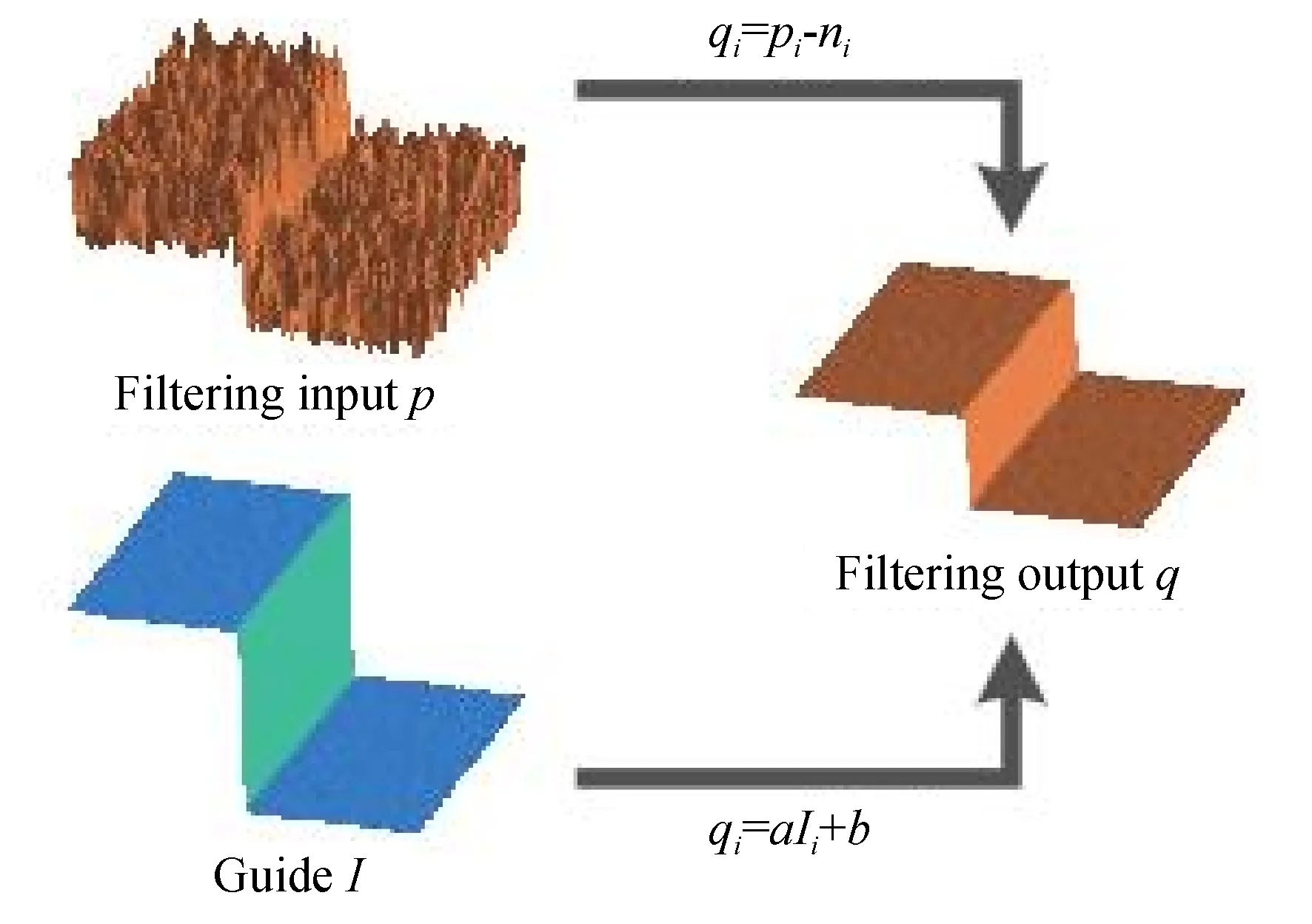
图2 引导滤波示意图Fig.2 Diagram of guided filter

2.3.1 引导滤波

He等[8]在2013年提出了一种局部线性滤波器即引导滤波器(Guided Filter,GF)，可以提供良好的保边滤波功能，尽量在减少输出图像的误差的同时也降低了时间复杂度，具有实时性。引导滤波的过程是线性可移可变的，包括引导图像I，输入图像p和输出图像q。因为引导滤波的良好性能，被广泛应用于图像去噪，图像增强及超分辨率重建等领域。图2为引导滤波示意图，主要原理就是将I的边缘信息和p的颜色信息整合，得到输出图像q。引导滤波的定义表达式如式(5)所示：

qi=akIi+bk,∀i∈ωk,

(5)

其中：i为像素索引；Ii为i坐标对应的引导图像；qi为i坐标对应的滤波输出图像；ak和bk是以像素k为中心的窗口wk的线性关系系数，ak和bk的求解需要满足如式(6)的代价函数：

(6)

其中：ε表示正则化参数；pi为滤波输入图像。其中：

(7)

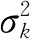
因为在计算的过程中，一个像素点i可能被包括在若干个窗口wk中，所以对窗口中所有可能值取平均，则滤波输出图像qi表示如下：

(8)

经过推导，滤波输出图像也表示为核函数形式[8]：

(9)

其中：i和j为像素索引；Wij(I)为滤波核函数矩阵，定义如下：

(10)

与双边滤波器相比，引导滤波器有了更高的性能提升。一方面，因为引导滤波的基本原理是梯度保持，即使在强度突变位置附近信号的个数较少，但只要有足够的梯度信息，就能够实现较好的跟随效果，有效抑制了双边滤波中出现的梯度翻转的现象，所以较好地保留了处理图像的边缘轮廓信息；另一方面，因为引导滤波核函数使用了邻域内像素的均值与方差作局部估计，其时间复杂度O(N)与窗口大小无关，这一点与高斯双边滤波核函数有本质的区别，因此，在处理较大的图片时效率有明显提升，可满足实时性要求。对于引导滤波(GF)的梯度保持功能的示意图[8]见图3，通过局部放大图像可以观察到引导滤波在信号突变区域也很好地跟随原信号。

综上分析，引导滤波可以代替双边滤波进行去噪及图像增强等。同理，也可以将其作为目标函数的空间平滑约束来正确估计照射分量，表示如式(11)所示：

(11)

图3 一维信号细节增强对比实验[8]Fig.3 Comparison of details for 1D signal enhanced[8]

2.3.2 快速引导滤波

He等[19]在2015年提出了快速引导滤波，该方法是在引导滤波的基础上对滤波图像I进行二次采样后再进行保边滤波。设二次采样比率为s，则时间复杂度会从O(N)降低到O(N/s2)，这可以带来>10倍的时间效率提升，并且滤波结果没有可见的退化。对于Algorithm1(Guided Filter)与Algorithm2(Fast Guided Filter)的计算过程和区别可以通过伪代码清楚地展示出来，具体内容如图4所示。

Algorithm1:GuidedFilter.1:meanI=fmean(I,r) meanp=fmean(p,r) corrI=fmean(I.*I,r) corrIp=fmean(I.*p,r)2:warI=corrI-meanI.*meanI covIp=corrIp-meanI.*meanp3:a=covIp./(warI+∈) b=meanp-a.*meanI4:meana=fmean(a,r) meanb=fmean(b,r)5:q=meana.*I+meanb

Algorithm2:FastGuidedFilter.1:I'=fsubsample(I,s) p'=fsubsample(p,s) r'=r/s2:meanI=fmean(I',r') meanp=fmean(p',r') corrI=fmean(I',*I',r') corrIp=fmean(I',*p',r')3:varI=corrI-meanI.*meanI covIp=corrIp-meanI.*meanp4:a=covIp./(varI+∈) b=meanp-a.*meanI5:meana=fmean(a,r') meanb=fmean(b,r')6:meana=fupsample(meana,s) meanb=fupsample(meanb,s)7:q=meana.*I+meanb

相较之引导滤波，最新提出的快速引导滤波在无明显退化的基础上实时性大幅提高，适用于兆像素图像滤波，所以本文提出将快速引导滤波作为目标函数的空间平滑约束项，来快速地估计照射分量。目标函数公式如式(12)所示：

(12)

其中：S为待滤波图像；S′为下采样之后的图像；W[m,n](S′)为下采样之后的图像的滤波核函数。

2.3.3 估计照射分量

对于基于快速引导滤波的变分Retinex目标函数的求解即式(12)的求解，本文通过雅克比(Jacobi)迭代来实现，包括以下三个步骤：

步骤1：计算目标函数的梯度

(13)

步骤2：计算目标函数的黑塞矩阵(Hessian Matrix)

(14)

步骤3：求解最小化目标函数

(15)

通过以上步骤就可以初步求取最小化的目标函数，也实现了基于快速引导滤波平滑约束的Retinex照射分量L′(x,y)的估计，再通过Retinex理论模型，便可以得到初步估计的反射分量R′(x,y)。

2.4 反射分量处理

由于获取到的雾霾图像有光照不均匀的特点，能见度低，图像看起来像蒙了一层模糊的透明板，此时使用快速引导滤波作为空间平滑约束项估计出来的照射分量有部分过于平滑，具有较高对比度的细节检测不出来，得到的初步估计反射分量R′(x,y)中含有照射分量估计的偏差和部分白噪声。因此，需要再对反射分量进行噪声抑制和细节增强。

分数阶微分是一种常用的图像增强算法，该算法相比于整数阶微分算法可以更好地检测模糊边界和微弱细节，调整图像的对比度，改善视觉质量。其中，该算子可在提升高频成分的时候非线性地保留信号中的低频成分，因此，使得增强后的图像细节更突出而且还保留了平滑区域的纹理信息。然而，因为图像的复杂性和多样性，使用单一的分数阶次对不同区域进行同等强度的处理，会导致增强后的图像局部失真，也会对噪声进行一定程度地增强。

通过以上分析，可以得知在图像增强的过程中，应当考虑图像的局部信息，因此，本文提出一种自适应分数阶微分算子对反射分量进行后处理，使其在图像强边缘处具有较大的阶数，在弱细节和纹理处具有较小的阶数，根据图像的局部信息和结构特征来自适应调整分数阶微分的阶数，更好地实现细节增强和噪声抑制，下面是自适应分数阶微分的介绍和构造。

目前分数阶微积分的定义主要有三种形式[22-23]：G-L定义( Grümwald-Letnikov, G-L)，R-L定义( Riemann-Liouville, R-L)和Capotu 定义。由于后两种计算复杂，不利于大规模计算，因此，本文选择分数阶微积微分G-L定义来进行介绍，其定义表达式如式(6)所示：

(16)

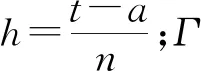
(iω)v·s(ω)=dv(ω)·s(ω).

(17)

由式(17)可以得到分数阶微分算子的幅频特性曲线如图5所示。

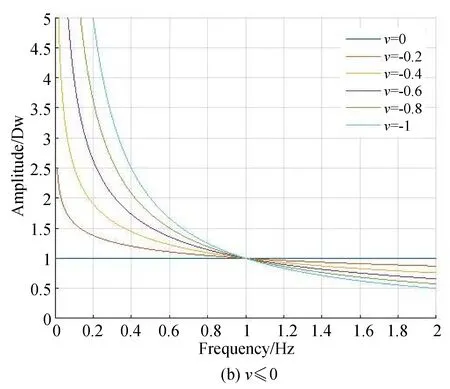
图5 分数阶微分算子幅频曲线Fig.5 Amplitude and frequency curves of fractional differential operator

由图5(a)可知，当分数阶微分阶数v>0时，其可以在提高高频信息的同时对低频信息进行非线性地保留，也就是说在增强图像的同时，一定程度地保留了平滑区域的纹理细节信息，使得增强后的图像细节信息更加清晰；由图5(b)可知，当分数阶微分阶数v<0时，其可以在提高信号低频信息的同时，对高频信息进行了非线性地保留，也就是说在抑制噪声的同时，一定程度地保留边缘区域的纹理细节信息，使得处理后的图像不会过于模糊。所以，借助分数阶微分的不同作用性质，再根据图像的局部特征和统计信息来动态调整分数阶数v，从而实现自适应的图像增强。

2.4.1 自适应函数

(a) 局部梯度

图像的局部梯度反映该区域图像的变化率。一般来说，图像局部梯度模值的大小与该区域是边缘和纹理细节的可能性的大小呈正相关，即图像的边缘和纹理细节区域的梯度模值比平滑区域的大。当该区域是纹理细节等区域时需要增强的幅度大，分数阶微分阶数也相对较大；当是平滑区域时，增强的幅度小，分数阶微分阶数也较小。

根据中心像素和邻域像素间的关系，可得像素点(i,j)的八邻域方向梯度模值如公式(18)所示。其中，公式(18)为像素点(i,j)的八邻域方向的梯度的模值，令式中方向梯度模值的最大值近似表示中心像素(i,j)的梯度模值，即：

|Iij|≈max{G0,G45,G90,G135,G180,G255,G200,G315}

(18)

需要注意的是，噪声点区域和纹理细节区域的梯度模值都较大，因此需要对噪声点进行判别，对其进行平滑处理来抑制增强图像的噪声。通常，噪声点都是随机的，在其周围极少能找到一个与其梯度模值大小相近的噪声点，然而边缘或细节像素点比较连续，在其周围可以找到与其梯度模值相近的点。因此，根据以上分析可以构造一个“噪声”判断函数，即：

(19)

(b) 局部信息熵

图像的信息熵E表示图像的所含信息量，即图像纹理的丰富程度。图像边缘和纹理区域的信息熵E大于平滑区域，也说明边缘和纹理区域的像素值变化比平滑区域更显著。为了计算图像局部信息量的大小，使分数阶微分阶数v可以自适应调整大小，因此，本文引入了局部信息熵的概念。

设w是大小为d×d(d≥3)并以像素点(i,j)为中心的矩形像素窗口，pij为图像中像素值Iij出现的概率，为了准确地统计图像中像素点与八邻域像素点的关系，动态调整分数阶阶数v，令d=3。则局部信息熵用公式表述如式(20)所示：

(20)

综上分析可得，分数阶微分的阶数需要根据局部梯度模值和局部信息熵的变化而随之自适应改变，并且分数阶微分阶数的大小与梯度模值和局部信息熵的大小成正比关系。因此，设图像局部梯度和局部信息熵对阶数的影响是同样关键的，可以构造式(21)来表示阶数v与梯度模值|Iij|和局部信息熵Eij的关系。

(21)

其中：k1和k2是调节系数，令k1=k2=0.5；vij表示求得的自适应分数阶微分的阶数；|和是归一化的局部梯度模值和局部信息熵，计算方法如式(22)所示：

(22)

2.4.2 自适应分数阶微分掩膜的构造

由于已经介绍过G-L定义，直接将其应用到二维图像信号I(i,j)中，将信号的持续期[a,t]按等间隔h=1划分，可以得到自适应分数阶微分算子在横轴和纵轴正方向的数值表达式如式(23)：

(23)

(24)

为了使用于图像增强的自适应分数阶微分算子满足旋转不变性和自相似性，考虑其横轴、纵轴和对角线等8个方向，构造出一个7×7的自适应分数阶微分掩膜算子如图6所示(空白区域为0)。

W3W3W3W2W2W2W1W1W1W3W2W1W0W1W2W3W1W1W1W2W2W2W3W3W3

其中滤波系数W为：

(25)

为了测试自适应分数阶微分处理对结果图像的影响，将原始雾霾图像、初始照射分量以及最终照射分量进行对比分析，其中包括2处图像细节放大图与实验图像的直方图，对比结果如图7所示。

由图7可以观察到原始雾霾图像经基于快速引导滤波的Retinex方法处理后得到的初始反射分量R′(x,y)除雾霾效果明显，细节提升较好，但是图像整体偏暗可视度较低。再经过自适应分数阶微分掩膜算子增强后得到的反射分量R(x,y)的对比度和亮度都显著提高，细节也更加清晰。另外，本文也对得到的反射分量分别计算直方图并进行分析，由图7(a)的直方图可以看到原始雾霾交通图像的灰度分布集中在中间值区域，所以原图对比度低且看起来灰蒙蒙的；由图7(b)的直方图观察到获取的初始反射分量灰度分布的动态范围扩大了；由图7(c)的直方图看到增强图像的动态范围再一次得到有效提升，对比度相应提高。

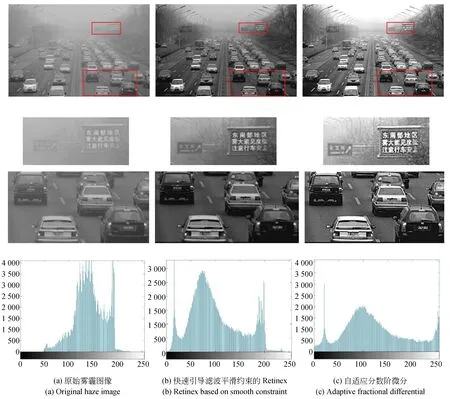
图7 自适应分数阶微分处理的对比Fig.7 Contrast of adaptive fractional differential processing

3 实验结果与分析

本文提出的结合快速引导滤波的Retinex和自适应分数阶微分的雾霾交通图像增强方法，其算法框图如图8所示，包含5个基本步骤：(1)将待增强的雾霾图像的颜色空间从RGB转换到YCbCr，提取亮度分量Y作为初始图像I′(x,y)；(2)利用基于快速引导滤波的Retinex算法估计初始照射分量L′(x,y)；(3)利用Retinex理论获得初始反射分量R′(x,y)；(4)采用自适应分数阶微分掩膜对R′(x,y)进行处理得到R(x,y)即Y分量的增强结果；(5)将增强后的反射分量与Cb，Cr色差信息结合，再从YCbCr转换到RGB颜色空间，即得到最终增强图像(Result I)。

为验证本文算法的有效性，本文选取了100多幅实际雾霾天气下的交通图像进行实验。本文算法中加权系数λ=0.10，正则化参数ε=0.12，引导滤波窗口半径r=64，二次采样比率s=4，自适应分数阶微分掩膜算子大小为7×7，实验环境为Inter i5处理器、Windows 7系统、内存大小8 G的计算机上进行，使用软件是Matlab2017a。由于篇幅有限，选取3组实验图像为例，并从客观和主观两方面进行对比分析，对比算法为CLAHE[4]，改进暗通道方法(Improved DCP)[20]，MSRCR[21]，ALTM[13]，分数阶微分方法(Fractional differential)[24]。

图8 算法基本框架Fig.8 Framework of algorithm

3.1 主观评价

本文选取的3组实验图像如图9所示，从左到右依次记为图9(a)～图9(c)。其中，图9(a)的原始图像雾霾情况比较轻微，自然光线受影响程度小、视野较亮且近景的交通信息对比度较高，而远景信息比如道路标识牌和电子显示屏能见度低。图9(b)的原始图像雾霾比较严重，图像不仅昏暗而且对比度极低，无法有效获取路况。图9(c)的原始图像获取时间是在傍晚且雾霾严重，因此该图像偏暗且亮度偏低，远景雾霾颜色更深。

图9 原始雾霾交通图像Fig.9 Original haze traffic images

其中，第1组的实验结果图如图10所示。图10(a)中图像对比度得到提升，细节信息增强，但近景信息过增强且远景信息中含有干扰噪声；图10(b)中图像的亮度得到有效提升，但去除雾霾效果不明显；图10(c)中图像产生了严重失真，视觉效果很差；图10(d)中图像的亮度信息有所提升，近景信息得到增强，但效果不太显著；与图10(d)相比，图10(e)中图像的纹理信息更加清晰，细节得到增强，但亮度较暗；图10(f)中图像质量明显提升，色彩更加逼真，对比度和清晰度更好，纹理细节信息明显。例如图10(f)中，汽车的车牌轮廓以及远景信息中道路指示牌的文字细节都清晰可见。

第2组的实验结果图如图11所示。图11(a)中图像对比度增加，纹理细节突出，但图像被过增强了，视觉效果较差；图11(b)中图像的近景信息比较明显，颜色失真小，但远处道路以及指示牌等依旧受雾霾影响严重；图11(c)中图像亮度提升明显，可视度增加，但去雾效果不明显；与图11(c)相比，图11(d)中图像的亮度信息提升明显，对比度和清晰度也较好，细节较清晰；图11(e)中图像亮度和色彩偏暗，视觉效果差，但纹理信息更加清晰，细节明显；图11(f)中图像质量色彩逼真，亮度较好地得到提升，细节清晰，可视距离更远且对比度更高。例如图11(f)中，远处的高架桥和LED灯牌信息清晰可见可辨别，车道线和道路边沿更加清楚。

图10 第1组实验结果图Fig.10 The first group of experimental results

图11 第2组实验结果图Fig.11 The second group of experimental results

第3组的实验结果图如图12所示。图12(a)中图像对比度显著提高，道路基础设施等细节清晰，但远景中天空区域出现光晕等噪声；图12(b)中图像的亮度得到有效提升，近景的车辆和道路信息明显，但远景中去除雾霾效果不明显，雾霾得不到有效去除；图12(c)中结果图像产生了色彩失真，视觉效果较差；图12(d)中图像的亮度信息有明显提升，对比度和清晰度较好，但天空区域过亮；图12(e)中图像的对比度和纹理细节得到增强，但亮度改善不明显，图像整体偏暗；图12(f)中图像对比度和清晰度明显提升，细节信息清晰，色彩信息更加真实自然。

图12 第3组实验结果图Fig.12 The third group of experimental results

3.2 客观评价

主观视觉分析可以快速直观地对增强后的图像质量进行评价，但由于个体主观感受的不同，做出的质量评价并不尽相同。因此，为了进一步验证所提出算法的性能，客观地评价增强后的无参考图像的增强质量，本文采用图像的信息熵(E)、亮度均值[25](AVE)、标准差(STD)、平均梯度(AG)和色调保真度[26](H)作为评价标准。

(1) 信息熵(E)，其表示图像中所含信息量的多少，值越大则说明图像所包含的信息越丰富。表达式如(26)所示，其中pijk的含义为，在通道k中pij像素值出现的概率：

(26)

(2) 亮度均值(AVE)，其表示图像的明暗程度，值越大则说明图像的亮度越大，视觉效果越明亮。表达式如(27)所示，其中I为所实验图像：

(27)

(3) 标准差(STD)，其表示图像中各个像素值与均值的离散程度，被用来客观评价无参考图像的质量，值越大则说明图像的质量越好。表达式如(28)所示，其中AVE为亮度均值：

(28)

(4) 平均梯度(AG)，其表示图像的清晰度和纹理细节的变化，值越大则说明图像的视觉效果越好，图像越清晰。表达式如(29)所示：

(29)

(30)

不同算法对雾霾交通图像增强的客观评价结果对比如表1所示，需要注意的是，为了方便分析增强前后图像色调的变化程度，在下表中将色调保真度指标H的结果放大了10倍。

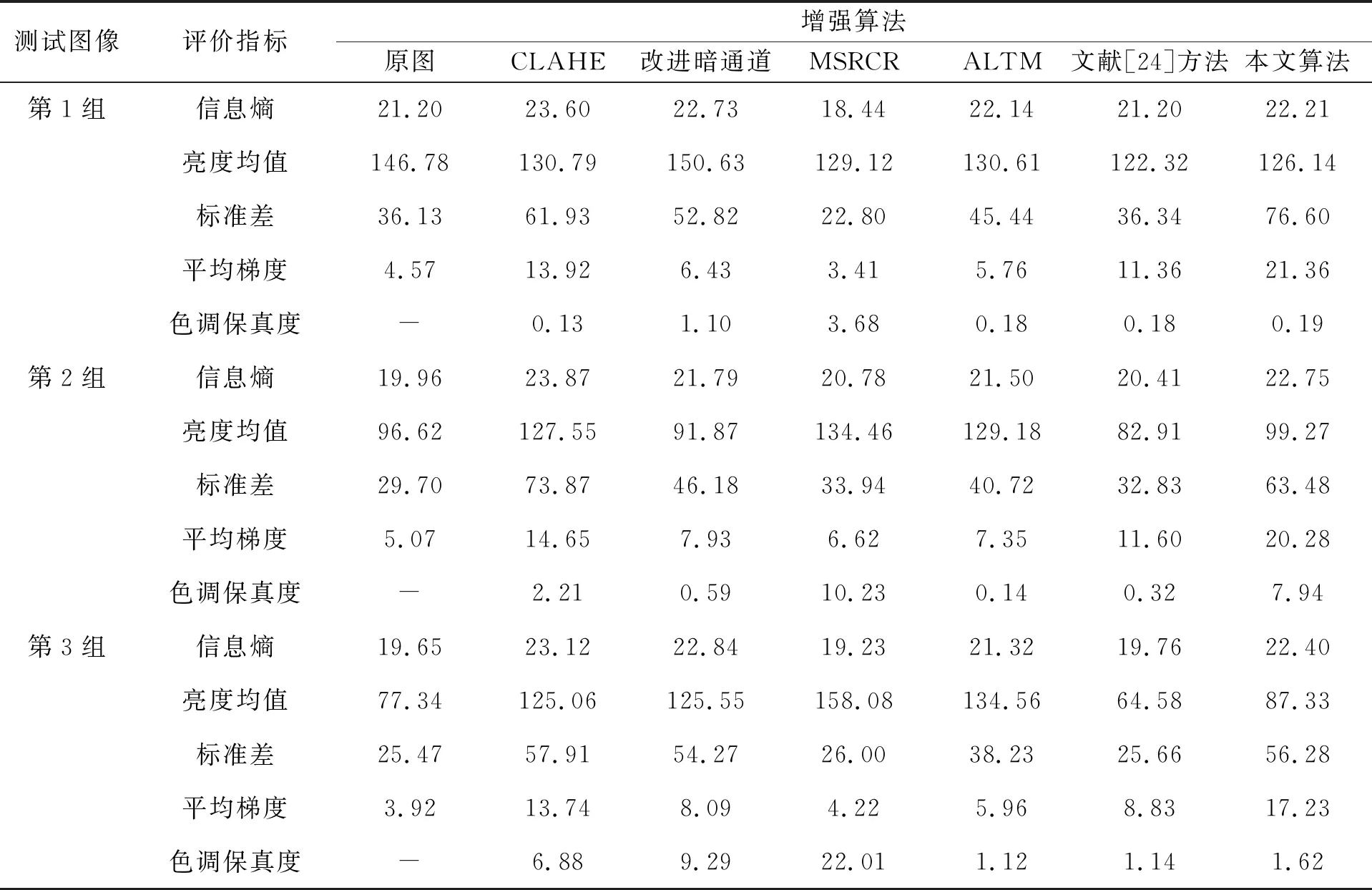
表1 不同算法对雾霾交通图像增强的客观评价结果对比

由表1的各项客观数据分析可知：对于第1组中亮度较高的轻度雾霾交通图像，MSRCR增强后的图像发生了严重失真，使图像的评价指标劣于原图。除此之外，对于3幅测试图像，本文算法与对比实验的其它算法均可以提高图像的信息熵，标准差和平均梯度，说明增强后的图像质量均得到一定的改善。新算法与CLAHE在上述3个评价指标方面的综合性能均优于改进暗通道、MSRCR，ALTM和文献[24]的方法，说明增强后的图像比其它方法的更加清晰，图像质量也更高，信息量也更丰富。对于本文算法与CLAHE，我们从另外其他2个指标(亮度均值与色调保真度)着手进行分析。首先，本文算法处理后的图像的亮度均值低于CLAHE，说明不论雾霾程度的大小，CLAHE增强后的图像都更加明亮一些，但对于雾霾严重的图像容易过增强。然后，对于色调保真度指标而言，新算法的综合性能优于CLAHE，增强后的图像色彩也更加逼真。值得一提的是，该算法在平均梯度方面的表现也显著优于CLAHE方法，即图像更加清晰，纹理细节等信息对比度更高。由客观评价指标可知，本文算法的标准差较原图提高1.12倍以上，平均梯度较原图提高4倍以上，信息熵至少提高4.76%以上，图像质量提升效果明显。

综上所述，本文提出的算法可以更好地用于提升图像的质量，提高对比度和清晰度，使得细节信息更加丰富。而且，该算法增强后的图像色彩更加接近真实值，色彩保真度较高。

4 结 论

为了提高雾霾天气条件下交通图像的对比度、清晰度和颜色保真度，改善图像的视觉效果，本文提出了一种采用快速引导滤波平滑约束的Retinex及自适应分数阶微分的雾霾天气交通图像增强算法。新算法的主要内容为：(1)为避免颜色失真，使得增强的图像更加自然，将原图从RGB转换到YCbCr颜色空间，提取亮度分量Y作为初始图像进行增强；(2)利用快速导向滤波良好的保边滤波功能和计算效率，将其作为平滑约束项求解变分Retinex来估计初始照射分量；(3)借助Retinex模型获得初始反射分量，再构造自适应分数阶微分掩膜算子来进行自适应增强，抑制噪声的同时更好地突出图像细节信息，得到增强后的反射分量；(4)将增强后的反射分量与Cb，Cr色差信息结合，再从YCbCr转换到RGB颜色空间，即得到最终增强图像。

本文对不同的雾霾交通图像进行主观分析和客观评价，由主观分析可知，新算法在图像增强和细节保持方面得到了很好的改进，清晰度和对比度提升显著，视觉效果好；由客观评价可知，新算法的标准差和平均梯度较原图至少分别提高1.12倍和4倍以上，信息熵至少提高4.76%以上。同时，增强图像的色调保真度失真较小，更加接近真实值。综上，新算法可以有效增强雾霾交通图像，提高图像的质量、对比度、清晰度，使得增强后的图像视觉效果和可视度明显改善，更加真实自然。