靶场适用的光电经纬仪光轴平行性检测

贾文武，刘培正，唐自力，张三喜，胡秋平

(中国华阴兵器试验中心，陕西 华阴 714200)

1 引 言

光电经纬仪广泛用于火箭、导弹和无人机等飞行目标的外弹道/航迹参数测量，是靶场主测设备之一。近年来，为了提高光电经纬仪遂行多样化测量任务的能力，迫切需要一种“可换负载式”光电经纬仪架构，根据不同的测试需求更换不同的成像探测组件以完成相应的测试任务。例如，通过在光电经纬仪上加装光谱成像仪可以完成目标光谱特性测量，通过在光电经纬仪上换装激光测距仪器可以实现对目标的单站定位测量等。但是更换成像探测组件后其光轴指向会发生变化，通常需要对光电经纬仪的光轴平行性进行检测，一方面依据检测值调整光轴指向以降低光轴不平行性误差；另一方面对光轴平行性误差进行修正以提高测量精度[1-3]。

目前，光轴平行性检测方法大多需要采用平行光管等专用仪器[4-7]，而靶场测试多在外场进行，很难满足专门的测试条件。现有的经纬仪的“三差”中的照准差虽然反应了成像光轴在水平方向上与理想照准轴的偏差[8]，但是其测量方法只能针对位于回转中心的单一光学系统。多光学系统之间的平行性检测必然涉及非回转中心的光学系统，因此难以实现对光轴平行性的检测。崔凯等人采用坐标变换法推导了望远镜探测系统与望远镜回转中心不重合情况下，探测系统的跟踪误差与两者位置偏差的关系[9]。王芳等人从成像系统像面脱靶量出发，基于坐标变换推导了成像系统无照准轴平行约束条件下的通用脱靶量合成公式[10]。上述方法均突破了对光学系统需要位于回转中心的限制，给成像光轴平行性检测方法提供了有益的借鉴。本文提出了一种基于方位标拍摄的光电经纬仪光轴平行性检测方法，可对位于经纬仪机架上不同位置的成像光轴平行性进行检测，有效解决了靶场试验条件下光电经纬仪光轴平行性检测的问题。

2 检测方法

2.1 光轴平行性的外场检测步骤

首先，引入涉及的三个坐标系：

一是测量坐标系(OM，XM，YM，ZM)。测量坐标系的原点为经纬仪回转中心；X轴为大地北，以北向为正方向；Y轴垂直于水平面，向上为正方向；Z轴与X轴、Y轴构成右手坐标系。

二是理想照准坐标系(OI，XI，YI，ZI)。理想照准坐标系的原点为经纬仪回转中心；X轴为经纬仪理想照准轴，其指向为正方向；Y轴为经纬仪的垂直轴，向上为正方向；Z轴为经纬仪的水平轴，向右为正方向。

三是成像坐标系(OC，XC，YC，ZC)。成像坐标系的原点为成像系统的投影中心；X轴为成像光轴，以成像方向为正向；Y轴为像面纵轴，正镜时向上为正方向；Z轴为像面横轴，正镜时向右为正方向。

当经纬仪的方位角和高低角均为零(经纬仪照准轴位于水平面内且指向大地北),理想照准坐标系与测量坐标系重合。

其次，在对光电经纬仪的成像光轴进行平行性检测之前，需要进行以下准备工作：

一是需要将光电经纬仪调平。

二是通过大地测量方法测量经纬仪回转中心和方位标十字丝中心(N)的坐标，这在靶场通常已经测量完毕。

三是在经纬仪成像光学系统更换或装调过程中，测量其投影中心(O)在理想照准坐标系下的坐标，设为(xo-i,yo-i,zo-i)。

最后，光电经纬仪光轴平行性外场检测的具体步骤如下：

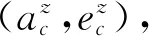
第三步，根据2.3节推导的光轴平行性检测公式计算成像光轴相对于理想照准光轴的指向偏差，从而实现对光电经纬仪光轴平行性的检测。

2.2 成像坐标系下三维坐标计算

光电经纬仪是高精度测角设备，通常只能测量目标的角度值，要对目标进行三维坐标测量还需要知道目标的距离。

目标距离的获取方法很多，比如激光测距、GPS定位等。对于靶场测量来讲，方位标、经纬仪回转中心的坐标已经通过大地测量等手段测量。因此，只需要在更换或装调过程中测量成像系统的投影中心位置，就可求出方位标十字丝中心与成像系统投影中心的距离。此时，结合图像判读测量出方位标十字丝的成像角度可以计算它在成像坐标系下的坐标。

在正镜状态下，方位标十字丝的坐标的计算公式为：

(1)

在倒镜状态下，方位标十字丝的坐标计算公式为：

(2)

2.3 平行性检测公式推导

假设成像光轴相对于理想照准轴在水平方向偏差为a，向右(顺时针)为正；高低方向偏差为e，向上(逆时针)为正。在正镜状态下对成像坐标系进行旋转和平移变换。首先成像坐标系绕Z轴顺时针旋转e角，再绕Y轴逆时针旋转a角，使得成像坐标系与理想主摄坐标系严格平行。其次将旋转后的成像坐标系平移到经纬仪回转中心与理想照准坐标系重合。此时可求出方位标十字丝中心在变换后的成像坐标系下的坐标如公式(3)所示。

在倒镜状态下对成像坐标系进行坐标旋转和平移变换。首先成像坐标系绕Z轴顺时针旋转e角，再绕Y轴逆时针旋转a角，使得成像坐标系与理想主摄坐标系严格平行。其次将旋转后的成像坐标系平移到经纬仪回转中心，使得变换后的成像坐标系与理想照准坐标系统成镜像关系。此时可求出方位标十字丝中心在变换后的成像坐标系下的坐标，如公式(4)所示。

(3)

(4)

由于正镜状态下成像坐标系经旋转、平移变换后与理想照准坐标系重合，倒镜状态下成像坐标系经旋转、平移变换后与理想照准坐标系重合但呈左右镜像关系，故方位标十字丝在两个坐标系下的坐标具有如下关系：

(5)

联立式(2)～式(4)可以得到式(6)。对式(6)中的第二项求解可得成像光轴相对理想照准轴在俯仰方向上的偏差计算公式(7)；对式(6)中的第三项求解可得成像光轴相对理想照准轴在水平方向上的偏差计算公式(8)，从而可以求出成像光轴相对于理想照准轴的偏差。

(6)

(7)

(8)

3 精度分析

对光轴平行性检测精度的影响因素包括，成像系统投影中心点的坐标测量精度、方位标十字丝与投影中心点的距离测量精度、经纬仪测角精度。

3.1 投影中心坐标测量误差对平行性测量精度的影响

经纬仪光学系统采用中心投影成像模型，所有指向目标的光线均经过该投影中心。通常认为投影中心为成像光学系统的节点，但是经纬仪的成像光学系统一般是由多组透镜、反射镜等构成，其节点位置难以精确测量。其坐标测量误差会对光轴平行性测量精度产生影响，需要进行分析。根据式(6)的第二项，利用隐函数求导法对投影中心Y方向上的坐标分量yo-i进行求导可得：

(9)

(10)

即投影中心在Y方向上的坐标测量误差主要对俯仰方向上的平行性检测精度产生影响，且距离越远，对精度的影响越小。

同理，根据式(6)的第三项，利用隐函数求导法对投影中心Z方向上的坐标分量zo-i进行求导可得：

(11)

同理，当方位标距离较远时且光轴平行性误差较小时sina≈0，sine≈0。式(11)可以近似为：

(12)

即投影中心在Z方向上的坐标测量误差主要对水平方向上的平行性检测精度产生影响，且距离越远，对精度的影响越小。根据式(10)和式(12)，当方位标距离1 km，投影中心坐标测量误差为1 cm时，引起角度偏差约为0.01 mrad(约2″)。

3.2 距离测量误差对平行性检测精度的影响

方位标相对成像系统投影中心的距离用于计算成像坐标系下的十字丝中心的坐标，其测量误差会对光轴平行性检测精度产生影响。联立式(1)，式(2)和式(6)的第二项，求出对距离Lz和Ld的偏微分，如式(13)所示。由于距离测量方法相同，因此测量误差δLz=δLd=δL，根据误差传播定律和式(13)，距离测量误差对俯仰方向上平行性检测精度的影响如式(14)所示。

(13)

(14)

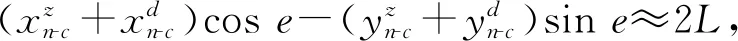
(15)

即方位标与投影中心的距离测量误差对平行性检测精度的影响也与方位标的距离有关，距离越远影响越小。比较式(15)和式(10)，在相同误差量级下，投影中心坐标的测量精度对俯仰方向上的平行性检测精度的影响远大于距离测量误差的影响。因此，当距离测量误差与投影中心坐标测量误差相当时，可不考虑距离测量误差的影响。

对于水平方向上的光轴平行性检测精度亦有类似的结论。

3.3 角度测量误差对平行性检测精度的影响

(16)

(17)

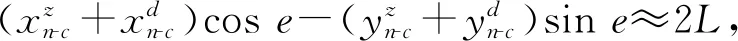
δe∝δ.

(18)

即俯仰方向上的平行性检测误差与角度测量误差相当且不受方位标距离的影响。对于水平方向上平行性检测精度的影响亦有类似的结论。

综上分析，投影中心坐标测量误差、方位标与投影中心的距离测量误差和成像系统的角度测量误差是影响平行性检测精度的主要因素。其中，投影中心的位置坐标测量精度、方位标与投影中心的距离测量精度均随方位标距离的增加而下降。在误差相等时，方位标与投影中心的距离测量误差对光轴平行性检测精度的影响远小于投影中心坐标的测量误差。当方位标距离为1 km，投影中心坐标测量误差为1 cm时，引起的角度偏差约为0.01 mrad(约2″)。成像系统的角度测量误差对平行性检测精度的影响不随距离的改变而改变，当方位标距离足够远时，它将成为影响平行性检测精度的主要误差。目前，光电经纬仪光学系统的角度测量精度可达3″，通过离焦成像等手段可以进一步提高其角度测量精度，因此其平行性检测精度可以达到很高的精度。而对于部分短焦成像系统，尽管其成像系统的测角误差较大，但是它能够在经纬仪上应用说明其测角精度是满足使用要求的，此时与其测角精度相当的平行性检测精度则通常也能够满足对该成像系统的平行性测量需求。

4 实 验

利用某型光电经纬仪进行实验验证，该光电经纬仪具有可见光测量、红外测量、红外捕获和监视电视4个成像光学系统，它们在经纬仪机架上的分布如图1所示。其中，除监视电视的焦距未进行标定，无法测量目标的角度值外，对可见光测量、红外测量、红外捕获系统的光轴平行性进行检测。

图1 经纬仪成像光学系统示意图Fig.1 Arrangement of imaging systems for photoelectric theodolite

根据设计指标，可见光测量系统的投影中心相对经纬仪回转中心的坐标为(0.0 m，0.150 m，0.000 m)，可见光相机像素当量(测角误差)为3.14″；红外测量系统的投影中心相对经纬仪回转中心的坐标为(0.0 m，-0.137 m，0.000 m)，红外测量相机像素当量(测角误差)为14.3″；红外捕获系统的投影中心相对经纬仪回转中心的坐标为(0.0 m，0.000 m，0.590 m)，红外捕获相机当量(测角误差)为41.3″。

同时根据大地测量结果，方位标相对于回转中心的坐标为(-82.526 m，-2.892 m，622.441 m)。因此根据第3节的分析，投影中心坐标测量精度为1 cm，坐标测量误差引起的平行性检测误差为3.3″。

根据误差传播规律，可见光系统光轴平行性的检测精度约为4.6″，红外测量系统光轴平行性的检测精度约为14.7″，红外捕获系统光轴平行性的检测精度约为41.4″。

在正镜状态下，旋转经纬仪对准方位标，可见光测量、红外测量、红外捕获分别拍摄图像如图2(a)、2(c)和2(e)所示。将经纬仪置于倒镜状态下，可见光测量、红外测量、红外捕获分别拍摄图像如图2(b)，2(d)和2(f)所示。

图2 方位标图像Fig.2 Image of azimuth marker

判读大靶板中间十字丝的中心相对视场中心的成像角度。其中正镜状态下可测得:可见光图像的成像角度为(-44.7″,-425.3″)，红外测量图像的成像角度为(21.5″,-257.8″)，红外捕获图像的成像角度为(-134.1″,-309.4″)。在倒镜状态下可测得可见光图像的成像角度为(-53.0″, 204.6″)，红外测量图像的成像角度为(1.8″, 350.9″)，红外捕获图像的成像角度为(-183.8″,-319.7″)。

由此可知，可见光光轴相对理想照准轴的偏差为(48.9″，61.1″)，红外测量光轴相对理想照准轴的偏差为(-11.6″，-1.5″)，红外捕获光轴相对理想照准轴的偏差为(-34.9″，-5.2″)。

由于可见光测量和红外测量位于经纬仪回转中心上下分布，它在水平方向上的偏差与经纬仪对应成像系统的照准差一致。通过三差测量方法测得的可见光测量系统的照准差为49.0″，与本文方法测量水平方向偏差48.9″相比，在误差范围内一致。而红外测量系统的照准差为-11.5″，与本文方法测量的水平方向偏差-11.6″相比，在误差范围内一致。而红外捕获系统位于回转中心右侧，因此它在俯仰方向上的偏差与红外捕获系统的零位差一致，通过三差测量方法测得红外捕获系统的零位差为-5.0″，与本文方法测量的俯仰方向上的偏差-5.2″相比，在误差范围内一致。从而验证了本文方法的正确性。

5 结 论

本文针对光电经纬仪光轴平行性靶场检测需求，提出了一种基于方位标拍摄的检测方法。通过坐标旋转变换公式推导出了光轴平行性检测公式，分析了成像系统投影中心坐标测量误差、方位标与投影中心的距离测量误差、成像系统的角度测量误差对平行性检测精度的影响。分析表明，成像系统投影中心坐标测量误差、方位标与投影中心的距离测量误差对光轴平行性检测误差随着方位标距离的增大而减小，当方位标距离为1 km、坐标测量误差为1 cm时，坐标测量误差和距离测量误差对平行性检测精度的影响约为0.01 mrad；当距离足够远时，平行性检测精度与成像系统的角度误差相当，能够满足靶场使用需求。最后，对某型光电经纬仪的可见光测量、红外测量、红外捕获系统的光轴平行性进行了检测。将位于经纬仪回转中心上下可见光测量和红外测量系统在水平方向上的平行性检测结果与其照准差检测结果分别进行比较，两种检测方法在误差范围内一致；将位于经纬仪回转中心右侧的红外捕获系统在俯仰方向上的平行性检测结果与其零位差的检测结果进行比较，两者在误差范围内一致，说明了本文方法的正确性。