非合作纹理目标单目位姿计算

冯肖维，谢安安，肖健梅，王锡淮

(上海海事大学 电气自动化系，上海 201306)

1 引 言

非合作目标位姿测量广泛应用于机器人环境感知、空间交会对接和虚拟现实等领域[1-4]。由于无法事先获得目标物体外形信息，使非合作目标位姿计算变得复杂与困难，必须首先恢复目标表面三维信息(如纹理特征、外形轮廓等)，然后利用这些信息提供的空间约束关系解算位姿[5]。

单目视觉系统无法直接获得景深信息，只能利用目标与相机间的相对运动来恢复场景三维结构(Structure From Motion，SFM)[6]。而单目位姿计算不仅要恢复目标三维结构，还需要实时精确估计相机与目标之间的相对位姿。Segal[7]首先恢复目标三维信息，然后利用扩展卡尔曼滤波算法迭代求解位姿，由于需要事先恢复目标的三维结构，无法实时在线应用。在一些非结构化应用场景中，由于无法事先恢复目标完整外形信息，只能根据逐渐恢复的目标三维表面结构信息来确定目标与相机间的相对位姿，此过程类似于同时定位与地图构建(Simultaneous Localization and Mapping，SLAM)[8]。Augenstein[9]利用粒子滤波实现目标同步三维重建与位姿估计，依靠粒子滤波的多假设估计提高算法抗干扰能力。为了实现目标特征和相对位姿的联合估计，前述方法需要滤波器对每帧图像进行处理，将时间消耗在处理具有极少新增信息的冗余图像帧中，且忽略了累积线性化误差。为此，Klein[4]和Mouragnon[10]提出基于关键帧的单目视觉方法，仅使用选定的图像帧重构三维信息，因此可以执行更费时但更准确的非线性优化。Strasdat等人证明在相同的计算成本下，基于关键帧的优化技术比滤波法更为准确[11]。

在单目视觉SLAM中，环境中的所有特征都可以用于解算位姿，当镜头移动时，连续图像帧之间存在丰富的共视特征，保证视觉SLAM具有较高稳定性与抗干扰能力。但在指定目标的位姿计算中，目标只占图像的局部区域，提取的特征数量有限，使得空间约束关系变少，算法的稳定性变差，特别是当背景特征丰富时，会进一步给目标特征辨识造成困难，导致计算失败。此外，单目视觉具有尺度漂移问题，目标模型在增量式恢复过程中会产生累积误差，进而影响位姿计算的精度。Mur-Artal等[8]利用关键帧思想增量式恢复环境三维共视特征地图，并依靠回环检测与位姿图优化保证地图尺度一致性，实现相机相对非结构环境的位姿计算，但是无法针对具体目标计算相对位姿。在此基础上，刘宗明等[12]实现非合作目标基于关键帧的纯旋转位姿测量，由于没有建立目标模型，无法分离前景与背景，因此该方法只能在结构化环境中使用。并且前述方法在优化时都只考虑成像模型约束，而没有考虑特征点与目标轮廓之间的几何关系。

非合作目标位姿计算的关键是如何在线恢复目标外形信息、抑制累积误差以及避免环境干扰。本文选择具有良好共视特性的图像帧——模型帧——构建共视特征模型，实现非合作纹理目标三维信息的合作化。利用网格模型对目标表面轮廓及其拓补关系进行估计，增量式恢复目标表面未知区域特征点与非共视特征点三维信息，增加模型包含特征的数量。并利用网格法向场引导特征模型的优化调整，减少由于网格近似造成的特征恢复误差，从而提高目标位姿的计算精度。在此基础上引入模型帧闭环优化，抑制尺度漂移形成的累积误差。依靠运动预测模型跟踪共视特征实现目标相对位姿的实时计算。

2 目标特征模型恢复

2.1 共视特征模型

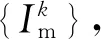
(1)

考虑实时性与尽可能多的引入视差，模型帧在选择时需要满足如下条件：

(1)模型帧的间隔大于15个连续图像帧；

(2)模型帧必须包含αm=40个以上目标表面特征点，从而提供尽可能多的约束条件，便于三维信息的恢复与优化；

(3)新增加的模型帧与某个已有模型帧之间共视特征的比率要小于βm=85%，使邻近模型帧之间具有较大的视觉变化，提高匹配特征之间的视差。

由于使用了共视特征模型，位姿计算与模型优化可以在局部区域进行，而与图像帧率无关。同时，为了控制共视特征模型M中模型帧的总体数量，每增加新的模型帧都会伴随冗余帧检测，剔除模型中特征匹配率高于γm=90%的模型帧，使得在增量式建模过程中可以灵活地扩展目标模型，当连续观测到目标表面相同区域时，模型无需被重复构建。

2.2 模型初始化

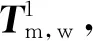
2.3 三维信息恢复

图1 特征点三维重构Fig.1 3D reconstruction of feature points

(2)

(3)

(4)

2.4 特征点的选择

为了只恢复目标表面的特征，本文利用网格模型F的拓扑关系对位于网格外的特征点进行筛选，避免背景特征加入共视特征模型。

(5)

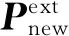
2.5 模型法向约束优化

由于三角网格模型是实际物体表面的一个近似逼近，因此根据网格模型重投影恢复的特征三维信息含有误差，影响位姿计算的精度。当共视特征模型被更新，即有新的模型帧被加入时，本文所述方法会对共视模型中与新加入模型帧具有共视关系的区域进行优化调整。

假设镜头无畸变，相机的内参矩阵为K，则成像模型π可以表示为：

(6)

其中si,k为尺度系数，取默认值si,k=1，则第i个特征点对第k个模型帧的重投影误差为：

(7)

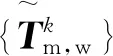
(8)

图2 特征模型局部优化Fig.2 Local optimization of feature model

如图2所示，目标表面三角网格模型F中局部区域f的某个三角面片f∈f的法向量为nf。则根据f中每个三角面片的法向量与其3条边之间的正交关系，定义如下优化正则项：

(9)

其中∂f表示面f对应的边。则最终的基于面法向场约束的模型局部优化表示为：

(10)

其中参数θ用于控制投影约束优化与模型法向约束优化之间的平衡。本文取θ=1，使重投影误差与法向调整误差具有相同重要性。本文使用Levenberg-Marquardt法进行非线性优化求解。

2.6 模型闭环尺度优化

如果相机再次采集到目标表面某个已建模区域，则可以通过模型中已建立的模型帧调整当前模型帧的尺度。

(11)

(12)

(13)

(14)

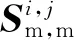
(15)

其中Λi,j=I7×7为误差项的协方差矩阵。

(16)

3 位姿跟踪计算

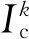
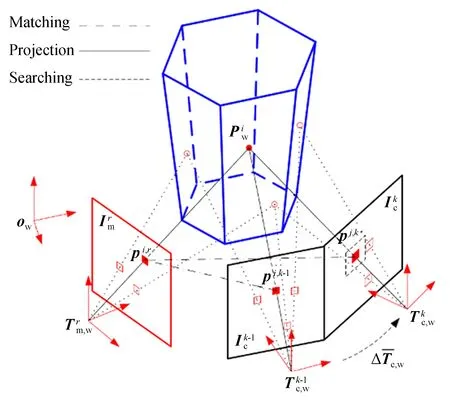
图3 特征共视关系的建立Fig.3 Establishing covisibility between features

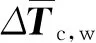
(17)

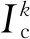
(18)

(19)

4 实验结果分析

实验中相机内参K已知，图像分辨率为640×480。程序用C++语言编写，运行于一台Intel core i5@2.40 GHz双核笔记本电脑，内存为8 GB，安装的操作系统为Ubuntu18.04 LTS。

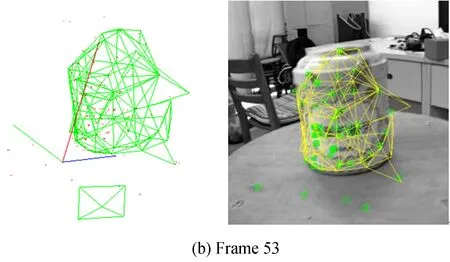
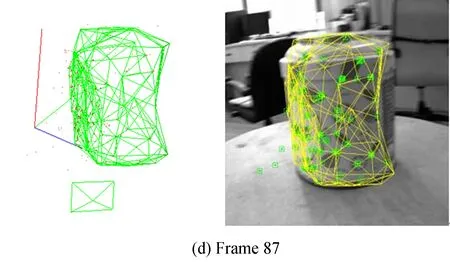
图4 圆筒增量式建模结果Fig.4 Incremental modelling results of cylinder

图4显示圆筒目标共视特征模型恢复过程(彩图见期刊电子版)。图左侧显示恢复的所有三维特征点，以及经过辨识后根据有效特征点构建的三维网格模型，绿色方框表示相机当前位姿。同时，将左侧三维网格模型根据计算出的目标位姿重投影到右侧对应二维图像帧上，右图中绿色小方框为提取的ORB特征。随着计算的推进，重投影网格与目标轮廓保持重合，说明本文所述方法可以对非合作目标进行在线同步建模与位姿计算。此外，图4(b)中有2个背景特征点被误加入模型，使模型产生了畸变，随着视角的变化，新信息的到来，干扰特征点被辨识，并从模型中剔除，如图4(c)所示，说明本文所述方法的特征选择机制可以有效区分目标与背景特征，从而保证只有目标表面的特征用于位置计算。

图5显示了图4所示建模过程中，模型帧的数量随时间变化的情况。本文所述方法的冗余帧回收机制使模型帧的数量保持在一个稳定的数量上，而不会随时间持续增长。同时由于目标识别机制，背景的变化并不会使新模型帧被加入，保证本文方法可以长时间高效运行。图中柱状图形表示不同时刻共视特征模型中每个模型帧的共视模型帧的平均数量，可以保持在5～10 frame之间，说明共视特征模型可以提供足够的特征进行位姿计算。

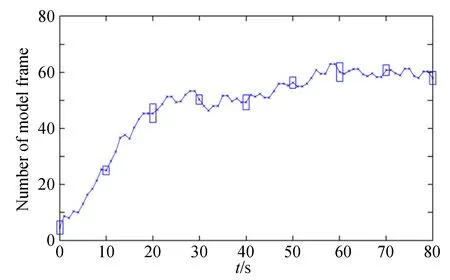
图5 模型帧数量及其共视关系的变化Fig.5 Evolution of the number of model frames and covisiblity

为了直观显示模型优化的效果，图6为目标三维网格模型在优化过程中的变化情况。可以发现，随着特征点不断优化，网格模型逐渐逼近真实目标轮廓，说明在建模过程中由于网格近似造成的特征恢复误差可以得到有效抑制。

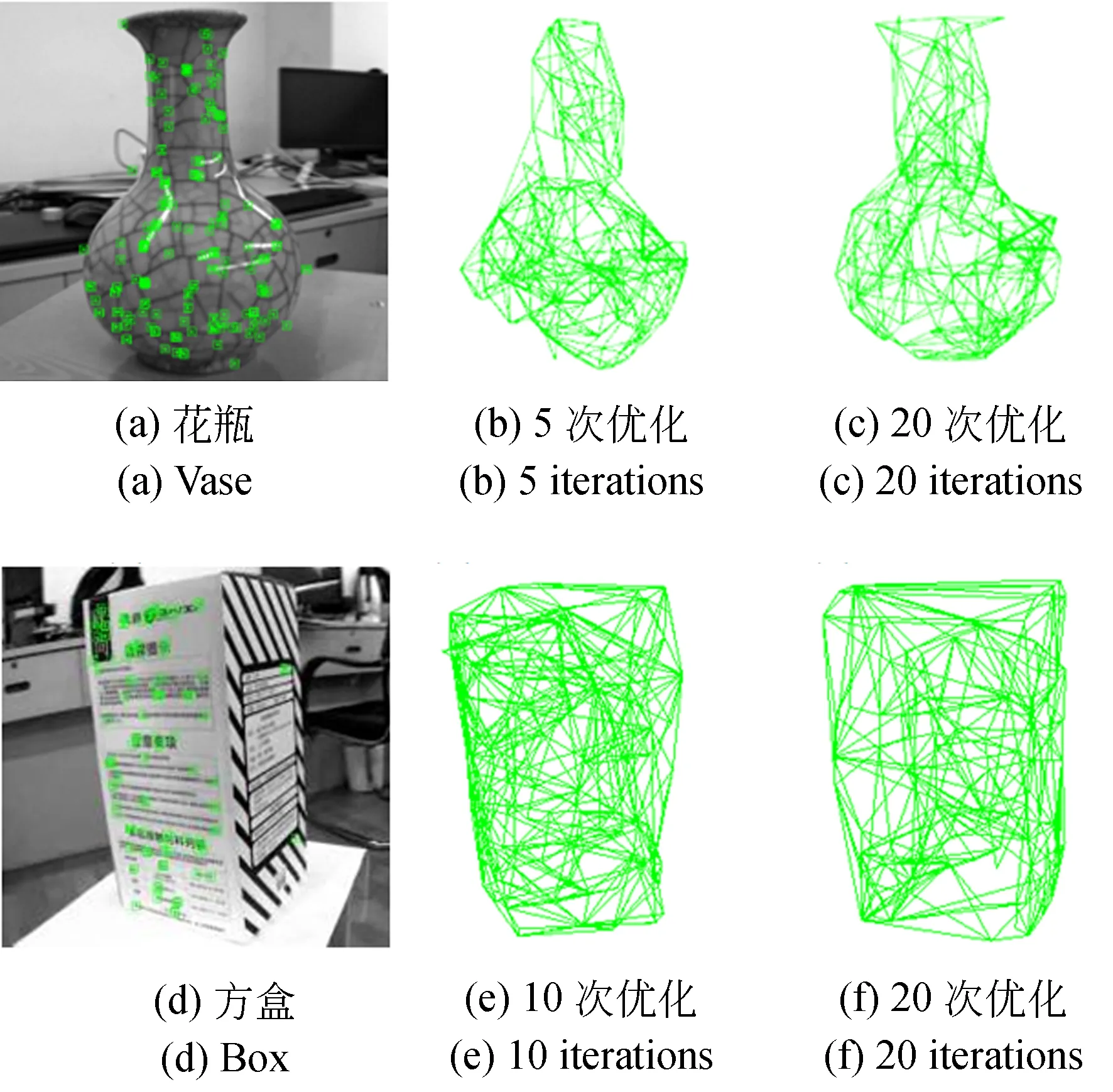
图6 目标网格模型优化结果Fig.6 Optimization results of target mesh model

图7显示了插入第40个模型帧后，模型优化前后特征模型恢复与特征重投影的结果(彩图见期刊电子版)。每幅图从左到右分别为特征模型与对应的真实目标外形线框模型、当前帧提取的特征点(绿色圆圈)和根据目标当前位姿得到的反投影特征点(红色交叉)及目标线框模型、特征重投影放大视图。图7(a)是未进行模型优化时的结果，由于初始估计的位姿与恢复的目标共视特征模型存在误差，重投影的特征与线框模型都与实际值具有较大偏差。图7(b)是模型经过无法向约束优化后的结果，通过共视特征点与位姿的优化，重投影误差得到明显改善，但是特征模型并没有收敛到目标真实轮廓。图7(c)是经过本文所述法向约束优化后的结果，重投影误差得到改善的同时，共视特征模型也得到优化，特征点朝着目标真实表面轮廓调整。

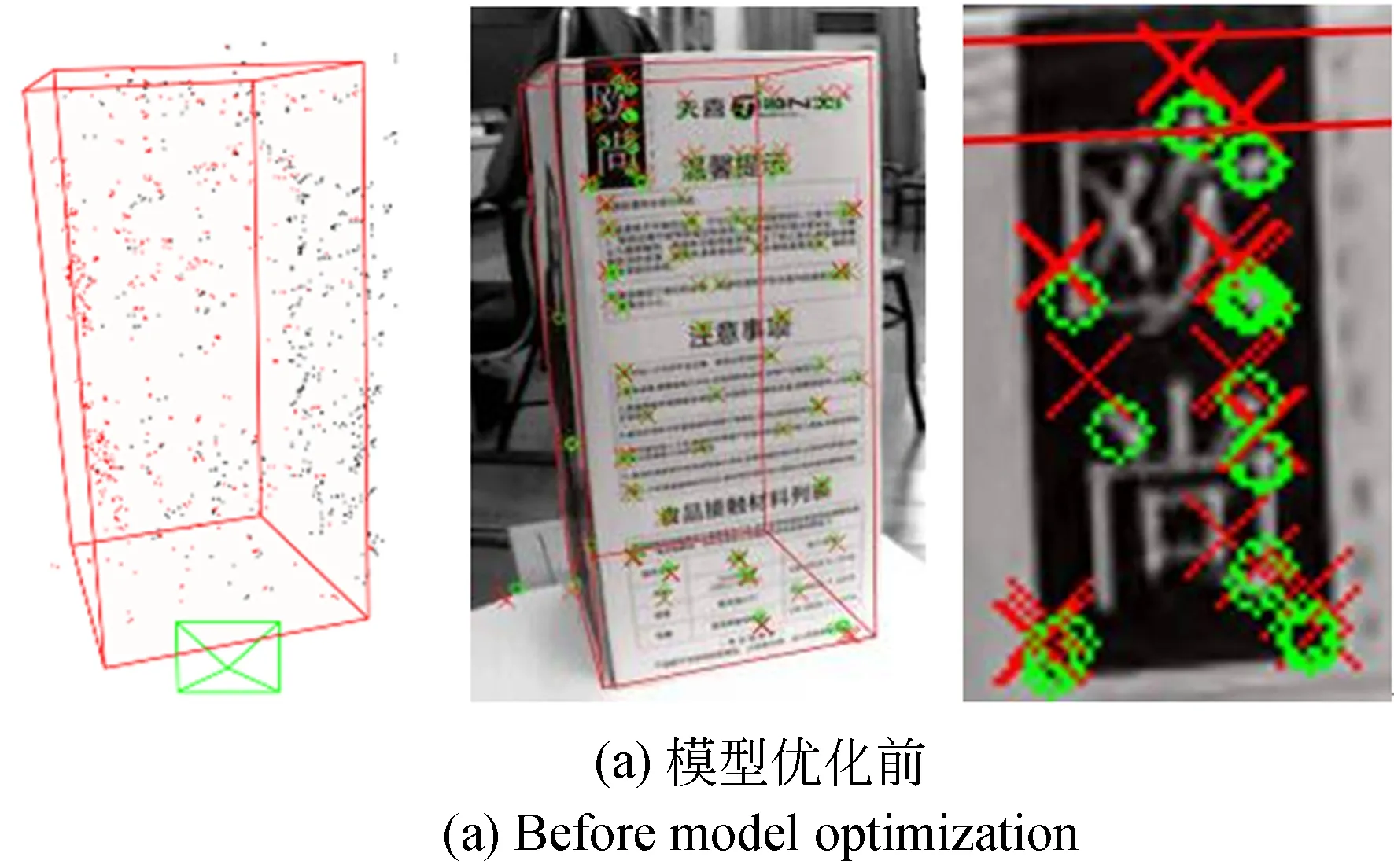
图7 特征模型与重投影误差比较Fig.7 Comparison of feature model and reprojection error

(20)

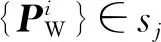
(21)

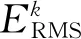
图8 特征重投影误差与偏离误差随优化的变化Fig.8 Evolution of reprojection error and normalized deviation error w.r.t. optimization

为了比较不同方法位姿计算精度，将多面体目标固定于高精度6自由度云台上做空间运动，利用固定于支架上的相机对目标进行连续拍摄，如图11所示。由于相机和目标之间的相对位姿真值未知，而云台提供的平移距离和旋转角度只能反映目标姿态的变化量，所以根据测量位姿的变化量来衡量位姿计算精度。

图9 精度分析实验平台Fig.9 Experiment platform of precision analysis

图10显示了，目标做20次位姿变换，平移距离变化量和旋转变化量的绝对和相对测量误差。将目标平移量测量值与对应云台平移量相比较，利用该比值对测量值进行尺度恢复后与云台实际平移量进行比较，得到平移误差。而旋转误差根据式(22)计算[16]：

(22)

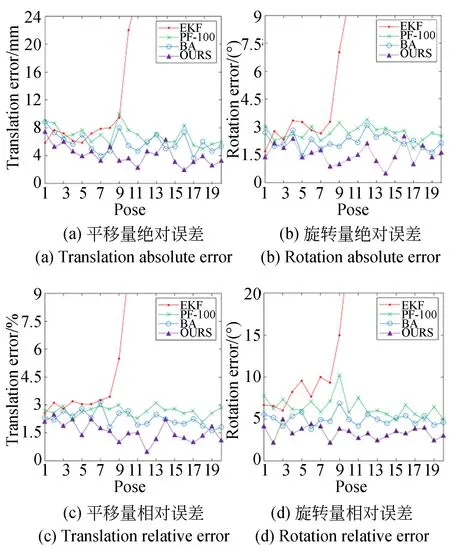
图10 回环优化对于共视特征模型的影响Fig.10 Influence of loop detection on covisibility

为了分析算法的时效性，对程序中各个功能模块的运行时间进行了统计，如表1所示。由于建模过程中网格数量是逐渐增长的，实验中等待模型帧数量稳定后再进行统计。从表中看出，位姿计算率维持在8 Hz，4个模块中最耗时的是网格构建，由于各模块采用多线程机制，因此其他3个模块对位姿计算的实时性影响较小。网格构建与模型优化过程中，当有新的模型帧插入时，局部优化会被终止，因此耗时变化较大。

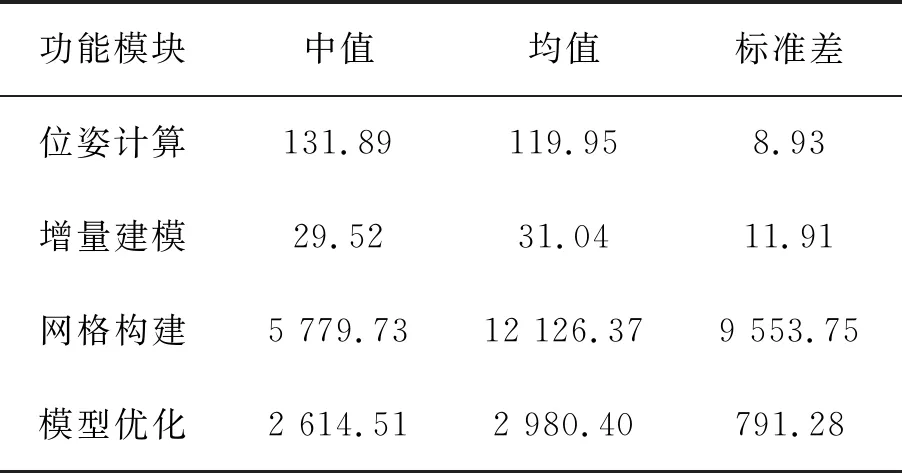
表1 位姿计算时效分析

5 结 论

本文根据机器视觉和计算机图形学相关理论，实现了非合作纹理目标在线同步建模与位姿计算。从连续图像帧序列中选择具有良好特征共视关系的图像帧构建基于ORB特征的共视特征模型，实现目标的合作化。利用网格模型指导目标未知区域特征点的增量式恢复，避免背景特征干扰和目标整体建模。在共视模型的局部重投影优化中引入法向约束，提高特征模型的恢复质量，并对模型进行闭环尺度优化，减少累积误差的同时提高位姿计算精度。实验结果表明，本文所述方法能够对非合作纹理目标进行实时的特征建模与位姿计算，为基于单目视觉的三维感知与测量建模提供一种有效方法。

在今后的研究中，可以考虑引入基于像素深度匹配的光流法进行非纹理目标的位姿计算；并利用如直线等特征施加更加稳定的空间约束关系，进一步提高算法的精度与稳定性。