小孔节流气体静压推力轴承微振动机理研究

王 伟，王 超，郑越青，崔海龙

(1.电子科技大学 机械与电气工程学院，四川 成都 611731;2.中国工程物理研究院 机械制造工艺研究所，四川 绵阳 621000)

1 引 言

“中国制造2025”提出我国要加快从制造大国转向制造强国，处于制造业顶端的精密、超精密加工装备成为必须要突破的技术瓶颈。作为超精密机床的核心部件—主轴及导轨决定了机床的加工性能，而轴承的性能又制约着主轴性能的提升。近年来，气体轴承区别于接触式和液体轴承成为了研究重点。气体静压轴承是气体轴承中应用最广泛的一类，主要原理是由外部气源供给的高压气体经节流后在相对运动部件间形成一层具有一定压力的气膜，从而支承部件所承受的载荷。其显著特点是相对运动部件间无直接的机械接触，工作时近零摩擦、磨损小、发热少、无污染、精度高且易于维护[1-2]。

小孔节流式气体静压轴承的相关研究已较为完善，其静动态性能仿真和测试方法非常丰富，这一类气体静压轴承设计准则已基本建立。而随着超精密领域加工精度的进一步提高，气体静压轴承存在的微振动问题对精度的影响已无法忽略，即使在恒定载荷作用下轴承的微振动仍存在。在改变节流器结构形状和均压槽形状对气浮轴承的优化效果渐渐失效时，提高气源供气压力作为提升气体静压轴承性能的优良办法，得到了大部分业内研究者的认同。但是提高气体静压轴承的气源供气压力，会加剧微振动的振幅，最后导致失稳现象，诱发气锤振动现象。国内外学者对微振动的研究由来已久，2007年，Shigeka Yoshimoto[3]提出由激波形成的轴承间隙内的复杂流体流动结构，发现气体从小孔流入轴承间隙后会产生湍流，而亚音速与超声速的交界处不会产生激波。2009年，Mohamed E. Eleshaky[4]通过计算流体动力学方法得到气膜的压力分布，并清晰地捕捉到小孔出口附近的流场相干结构，通过对激波结构的分解解释了气体压力突降现象；T. Aoyama等[5]发现空气静压导轨的加工精度在进入纳米量级时也受到了微振动的限制，于是通过改进节流器结构并在出口设置圆角均能有效地抑制微振动的幅度。2011年，陈学冬[6]团队对设计的不同形状的凹槽进行仿真和实验验证说明静压轴承纳米级别的振动与凹槽内的空气涡流存在一定的联系且球形凹槽在相同条件下的优越性。2012年，Tomotaka Yoshimura[7]探寻了静压轴承支撑物体产生纳米波动的原因，通过仿真计算和实验的综合验证得出了雷诺数与微振动的联系，发现低雷诺数条件下可以减小波动。2014年，陈琦等[8]发现均压槽的引入可以有效抑制微振动的产生。2017年，李运堂等[9]在均压腔内设计了一种流场扰动结构用以抑制微振动，并通过仿真和实验验证了结构的合理性。微振动的形成与气体静压轴承小孔出口附近的气旋结构有着直接联系，研究气旋产生的原因和轴承结构参数的联系就有着工程意义。

王云飞[10]于1997年提出了气锤振动的三个要素：具有一定大小的内部气容，具有激励振源和内部压强。而气锤振动可以说是微振动进一步发展而产生的，所以本文将从微观流场的角度验证这三个因素对于微振动的影响。近年来，众多学者也从不同角度探究了轴承参数对轴承性能的影响规律。2013年，孔中科等[11]研究了不同尺寸比例下的圆形和锥型压力腔气体静压轴承的气旋强度分布规律。2015年，夏毅敏等[12]探究了节流器结构参数对液体静压导轨轴承承载特性的影响，而气体静压轴承中均压腔结构的结构参数对承载性能有着更深远的影响。孙昂等[13]研究了不同轴承结构参数时的压力分布，承载力和气容比及其对轴承承载力和刚度的影响。2017年，赵艳凤等[14]研究了不同均压槽结构形状对静压干气密封性能的影响。2018年，赵晓龙等[15]发现变截面节流器的设计能有效提高轴承静承载特性。2019年，林晓亮等[16]研究了不同几何尺寸的纬线和经线槽对气体球轴承轴向承载力的影响；车健等[17]通过大涡模拟研究了不同节流孔形状对出口压力波动的影响。2020年，Li Chenhao等[18]在石油工业领域发表了气容与压力波动和内部流动特性关系的相关文章，这对研究气体静压轴承有一定的借鉴作用。轴承结构的改变实质上都是改变了气体静压轴承的气容，围绕同一结构不同参数下作微观流场分析研究流场对振动的影响就有了意义。

分析气体静压轴承的内部流场变化方式随着计算机性能的提高和计算软件的日益丰富而选择多样化。目前对静压气体轴承的仿真研究中大多停留在承载特性以及运动性能方面，较少地关注微观流场本身的变化。稳态流场特性无法描述湍流细节，只有瞬时湍流脉动细节及复杂涡结构的解析和描述才有希望从本质上解释微振动，相比雷诺平均方程(Reynolds Equation,RANS)的无法计算各尺度的湍流脉动，大涡模拟(Large Eddy Simulation,LES)是近年来发展较快并广泛应用于复杂湍流模拟的一种有效手段，虽比不上直接数值模拟(Direct Numerical Simulation,DNS)的精度，但是计算量和对计算机的要求却相对低，而且其对复杂湍流的模拟已经足以应用于气体静压轴承。2013年，陈学冬[19]团队的朱襟成采用LES对气膜流场进行了仿真分析，观察其内部复杂湍流流场和涡旋结构，将压力波动和轴承振动初步建立关系；李运堂等[20]通过大涡模拟分析了止推轴承的振动特性。2017年，陈学冬等[21]提出一种新型的阵列式微孔节流器，测试其结构效果仍然采用LES仿真来观察流场瞬态流动特性。2018年，范酬等[22]在研究气体静压径向轴承的动态性能时，也采用了LES方法，得到了明显优于RANS的结果，分析了轴承各参数对轴承振动的一定影响关系。2020年，Le Quang Phan等[23]也采用大涡模拟方法对冲击射流进行了涡旋动力学分析和波动观察，气体静压轴承中气体经小孔高速进入均压腔及气膜也可以看作为冲击射流运动。本文将通过LES模型对气体静压轴承作微观流场分析，从微观角度来与宏观振动相联系。2020年，徐抒岩等[24]利用仿真软件Fluent提出了一种方法可有效抑制气流扰动对于光学检测精度的影响，以此可以借鉴使用该软件来分析气体静压轴承的微观流场。

2 基本方程

大涡模拟的基本思想是通过密度加权过滤(Favre过滤)将湍流中的瞬时脉动分解为大尺度脉动和小尺度脉动，大尺度脉动利用可解尺度的Navier-Stokes 方程直接求得，小尺度脉动用亚格子应力模型进行模拟。本文采用LES模型，采用可压缩湍流大涡模拟控制方程来求解一定尺度湍流方程，以下为滤波后得到的连续方程、动量方程和能量方程[25]：

(1)

(2)

(3)

其中：上标“-”和“～”分别为空间滤波和Favre滤波，ρ为密度，ui和uj为速度，p为压力，e为总能，亚格子应力项为:

(4)

以过滤速度和温度为参数的分子黏性应力项:

(5)

可解尺度导热项为:

(6)

过滤后的可压缩流体的能量方程比较复杂，有更多的不封闭项，需要附加亚格子模式来进行数值模拟。亚格子应力模型的模式很多，经典的有Smargorinsky-Lilly模式、动态Smargorinsky-Lilly模式和亚格子湍动能模式，本文采用ANSYS Fluent大涡模拟计算中的WALE模式。大涡数值模拟并不求解亚格子运动，而是导出亚格子运动方程，用于可求解尺度运动和亚格子运动之间的能量交换过程。

3 建模及仿真参数设置

3.1 建立模型及仿真分组

为了保证小孔节流设计条件，需满足限制条件h3>d12/4d2和h3>d1/4-h2，保证节流形式不会变为环面节流。

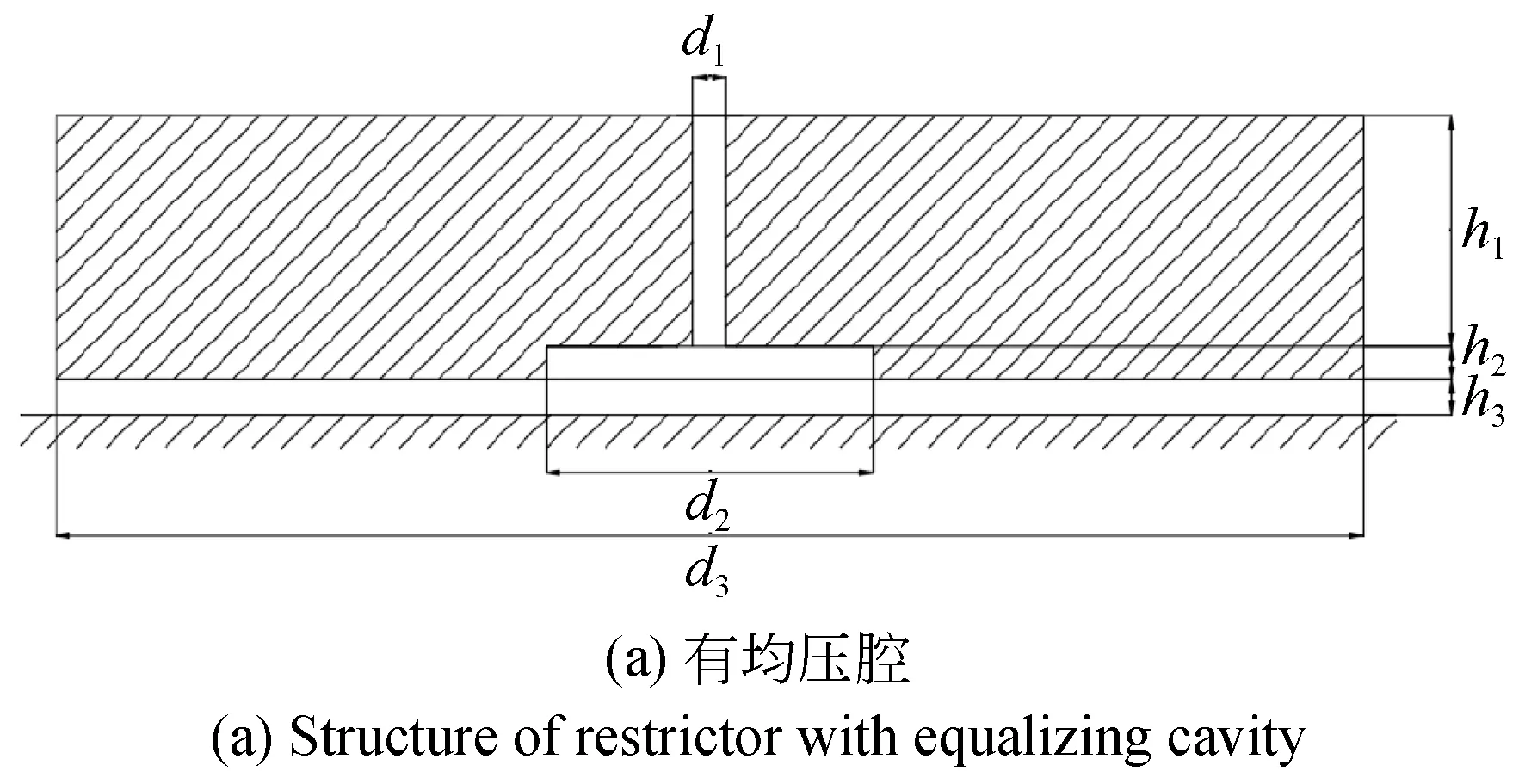
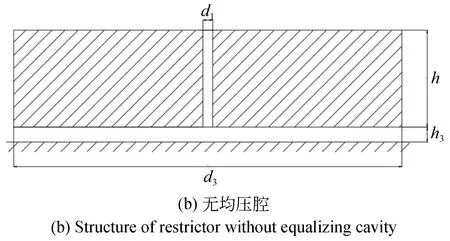
图1 静压气体推力轴承小孔节流器结构Fig.1 Structure of orifice restrictor of aerostatic thrust bearing

具有中心进气孔的有腔小孔节流静压气体推力轴承结构如图1(a)所示，对应的无腔结构为图1(b)所示。仿真实验组一和实验组二中，使用的第1组轴承基本参数为：节流孔直径为d1=0.03 mm，节流孔高度为h1=0.06 mm，均压腔直径分别为d2=0.6 mm，均压腔高度为h2=0.02 mm，轴承直径为d3=10 mm，气膜厚度为h3=0.01 mm，其对应的无腔小孔节流结构中的节流孔高度为h=h1+h2=0.08 mm。这两组仿真实验均为低相对气容比(<5%)下的设计，以小孔节流公式为限制条件，仿真实验组一中均压腔直径d2从0.3 mm变化至1.5 mm，仿真实验组二中均压腔高度h2从0.01 mm变化至0.03 mm，其节流孔高度h1相应地从0.07 mm变化至0.05 mm，满足h1+h2=0.08 mm，这是为了维持轴承整体的结构一致，使仿真实验组的对比具有实际意义。

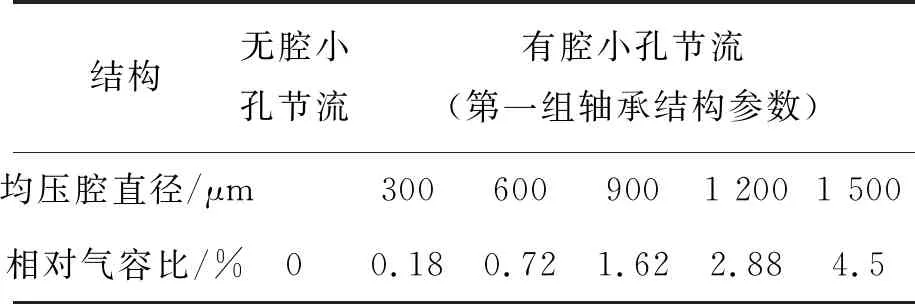
表1 均压腔直径对比仿真实验组一

前2组仿真实验组中所有结构节流形式均为小孔节流，而相应的轴承结构在实际中以现有的超精密制造水平还难以完全加工，因此后两组仿真实验的结构参数为实际可以加工的参数为基准进行的修正，在满足小孔节流下的不变基准下进行参数变化，在维持轴承整体结构一致的条件下，无腔小孔节流退化为环面节流，这也是所有仿真实验组中唯一一个环面节流结构。仿真实验组三和实验组四中，使用的第2组轴承基本参数为：节流孔直径为d1=0.15 mm，节流孔高度为h1=0.3 mm，均压腔直径分别为d2=3.0 mm，均压腔高度为h2=0.1mm，轴承直径为d3=20 mm，气膜厚度为h3=0.015 mm，其对应的无腔环面结构的节流孔高度为h=h1+h2=0.4 mm。这两组仿真实验均为高相对气容比(5%～21%)下的设计，以小孔节流公式为限制条件，仿真实验组三中均压腔直径d2从2 mm变化至3 mm，仿真实验组二中均压腔高度h2从0.06 mm变化至0.14 mm，其节流孔高度h1相应地从0.34 mm变化至0.26 mm，满足h1+h2=0.4 mm。

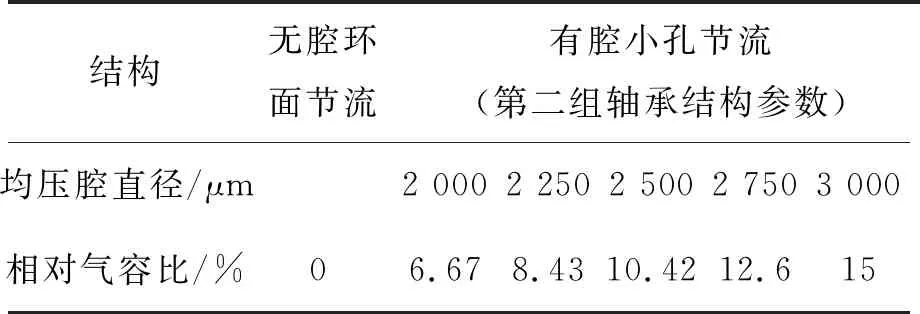
表3 均压腔直径对比仿真实验组三

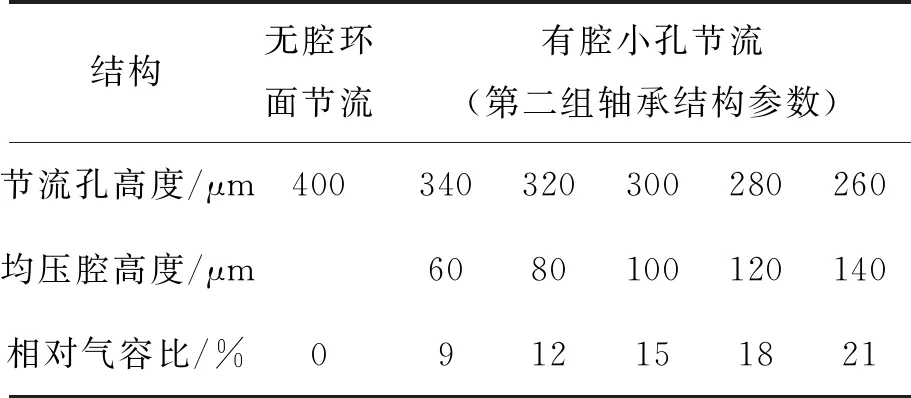
表4 均压腔高度对比仿真实验组四

前4组仿真实验需要综合分析，其唯一的共同参考要素就是气容比，前两组都属于低气容比，后两组属于高气容比，观察四组结果可以定量地得出气容比对气体静压轴承微观流场以及压力分布的影响规律。在改变均压腔直径和深度的仿真实验中，观察仿真实验组一和三以及二和四，可以得到单一结构参数在简单流态和复杂湍流下对流场的影响规律；观察仿真实验组一和二以及实验组三和四，可以得到不同结构参数在一定相对气容范围内的影响差异。仿真实验组五采用第二组轴承结构参数，单一变量为供气压力(0.5，0.6，0.7，0.8，0.9，1.0 MPa)，用以分析这一参数对微观流场的影响。

3.2 网格划分

模型建立完成后对模型进行网格划分，因为LES模型的计算量级要远高于RANS模型，所以基于结构对称性，只分析气体流场沿周向分布的十二等分之一。这里采用分块划分网格，如图2所示将流场划分为3个区域：节流孔区域，均压腔区域和气膜区域，对于节流孔和气膜区域，流场均处于较为稳定的状态，因此采用RANS模型，划分网格时不需要进行网格加密处理，而均压腔区域流场极为复杂，为了捕捉一定尺度的涡旋结构，采用LES模型，进行网格加密处理，即整个流场采用非一致网格用以节省计算资源和计算时间。

3.3 边界条件及初始化

如图2所示，定义气体压力入口(Pressure inlet)为节流孔入口，气体压力出口(Pressure outlet)为气膜出口，两个周向截面为对称边界(Symmetry)，其余外表面均为固体壁面(Wall)，因为采用非一致网格，所以节流孔、均压腔和气膜三个区域的两个交界面(Interface)也必须定义以进行数据交换。

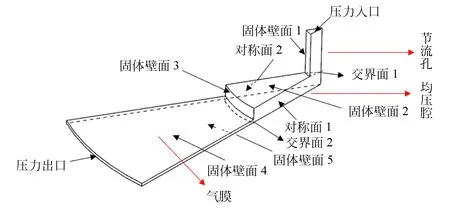
图2 小孔节流静压气体推力轴承仿真结构Fig.2 Model of orifice throttle aerostatic thrust bearing

3.4 求解计算

在进行LES计算前，先需要采用RANS模型进行稳态计算以获得流场的稳态解。这里选用基于压力的求解器，采用湍流模型中的Realizable-K-ε进行湍流稳态计算分析，气体选取可压缩流体，气体常数为一般取值，选用SIMPIE算法进行压力速度耦合计算，采用二阶迎风格式以获得更好的计算精度。实验组一至实验组四设定进口压力为0.8 Mpa，压力出口边界条件为0 Mpa，操作条件为一个大气压；实验组五设定进口压力为0.3～1.0 Mpa。

得到稳态初解后可进行LES计算，这里采用瞬态格式，选用LES模型中的WALL亚格子模式，边界条件保持不变，采用PISO算法，动量采用边界中心差分格式，其他仍采用二阶迎风格式，时间离散采用二阶隐式格式并用NITA格式加速计算，计算时间步长取Δt=1×10-8s(满足CFL条件，即运算速度快于运动速度，CFL=uΔt/Δx<1)。

4 测量实验与结果

当气体静压轴承内部相对气容超过一定比例时，会出现微振动现象。设计不同气容比的单孔小孔节流平板推力轴承结构进行对比实验，观察不同气容比下的轴承气膜微观流场可以对微振动的发生有着本质的理解。

4.1 均压腔直径对比仿真实验组一

仿真实验组一中有腔气体静压轴承只改变均压腔直径，相对气容从0.18%增至4.5%；图3是仿真实验组一的三维流线图，可以看出无腔小孔节流形式的气体轴承，从小孔到气膜，气体流动都很稳定，一直都是层流状态，没有明显涡旋存在；有腔小孔节流的结构仿真结果显示，流场开始从稳定层流向复杂湍流过渡，整体仍比较平稳。在不改变其他参数条件下，均压腔直径的持续增加虽然会加剧流场发展，但增加到一定程度时，流场的不稳定性并不会进一步扩散，都集中在均压腔区域，反而节流效果会下降。所以均压腔直径不适宜太小，流场的转捩会扩散到气膜区域；不适宜太大，节流效果会下降。

图4是仿真实验组一气膜径向压力分布图，其分布规律类似，气膜中心是压力最高点，然后沿径向先迅速下降，在扩散至均压腔后略有回升，最后平稳扩散至气膜边缘，无压力波动区域。无腔小孔节流结构在节流孔出口存在负压力区域，增加均压腔结构后消失。

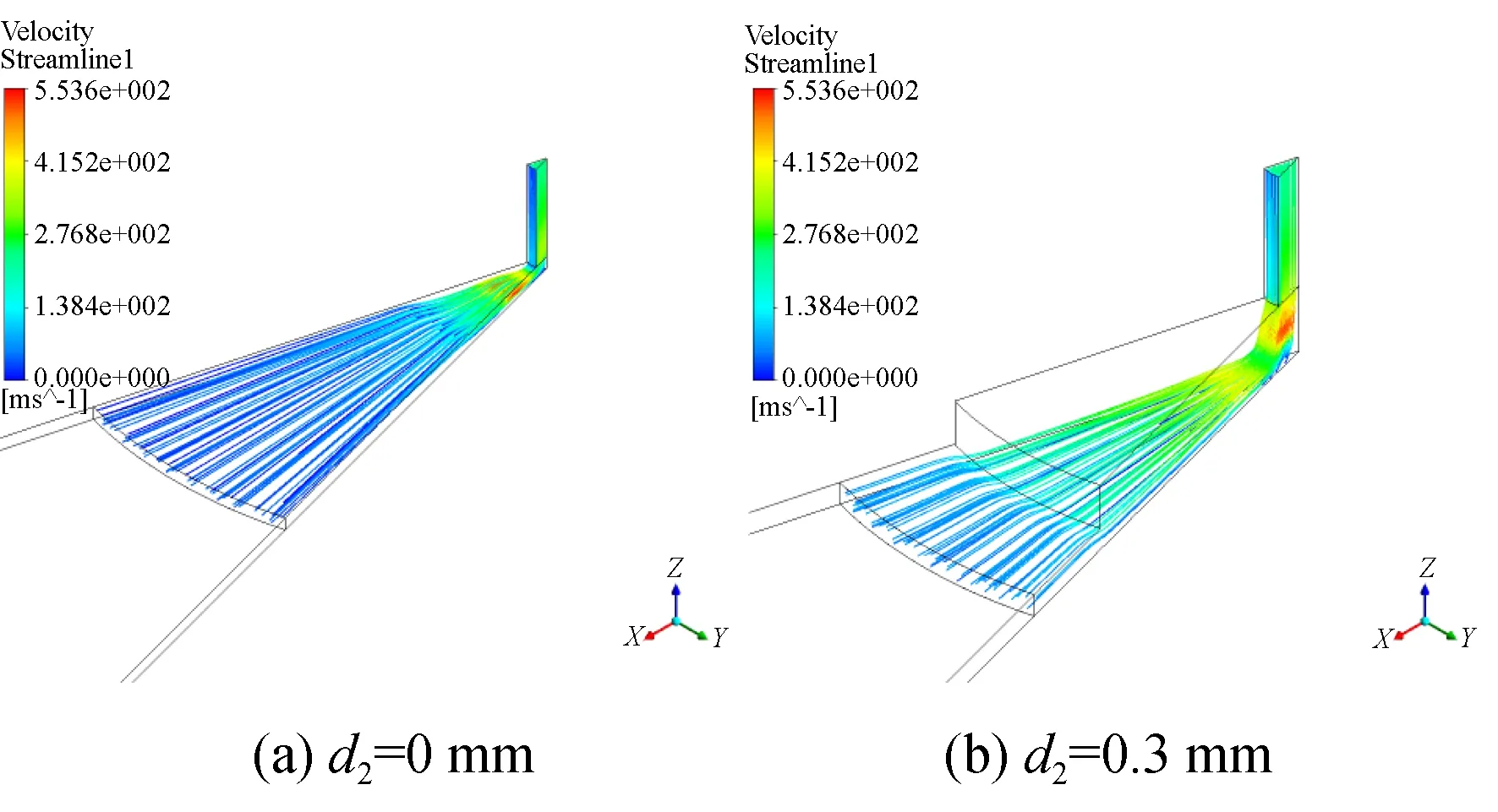
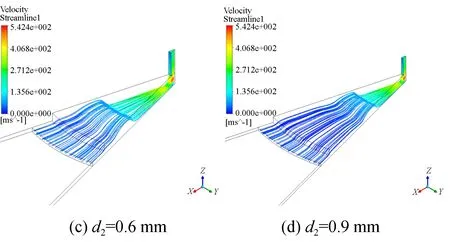
图3 仿真实验组一10 ms时刻三维流线图Fig.3 Three-dimensional flow diagram of comparison group 1 at 10 ms

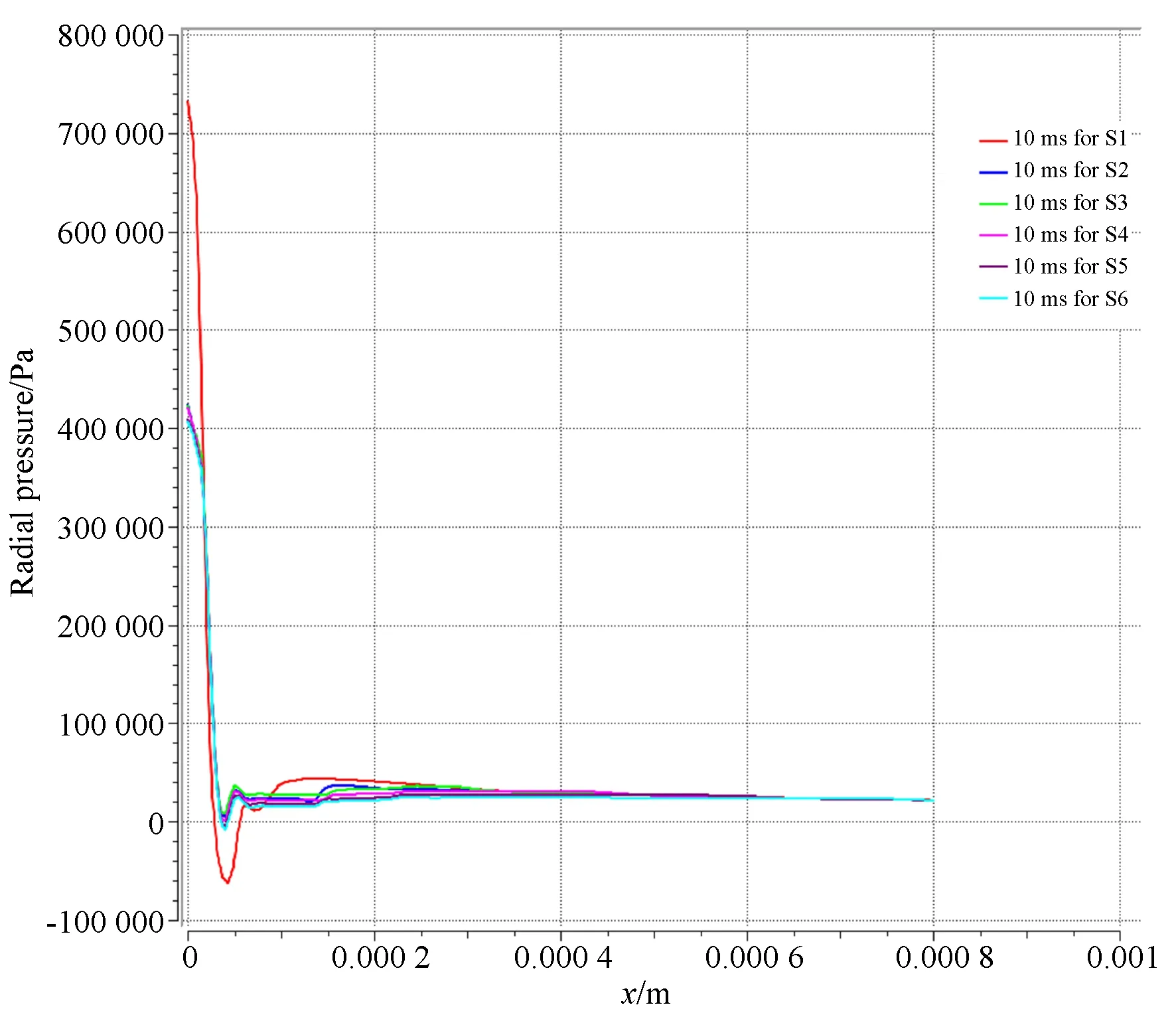
图4 仿真实验组一10 ms时刻气膜径向压力分布图Fig.4 Radial pressure distribution of gas film of comparison group 1 at 10 ms

4.2 均压腔高度对比仿真实验组二

以d2=0.6 mm的结构为参照，不改变其它参数，只改变均压腔高度，相对气容从0.36%增至1.08%。图5是仿真实验组二的三维流线图，可以看出，在不改变其他参数条件下，均压腔深度的持续增加同样会加剧流场发展，流场不稳定性会随着深度的增加而增加，相比仿真实验组一，深度的增加相比直径的增加对流场的影响更明显。

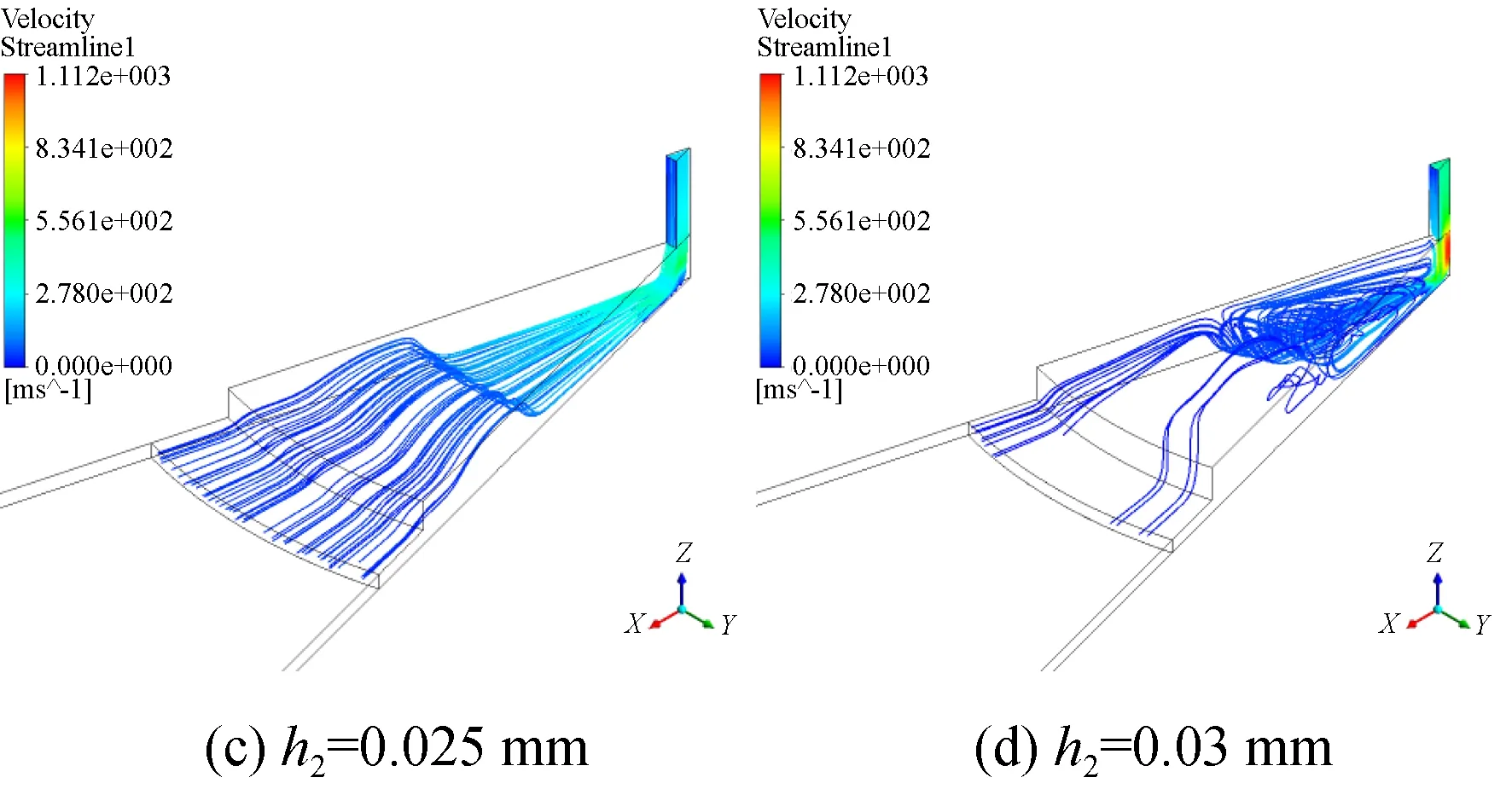
图5 仿真实验组二10 ms时刻三维流线图Fig.5 Three-dimensional flow diagram of comparison group 2 at 10 ms

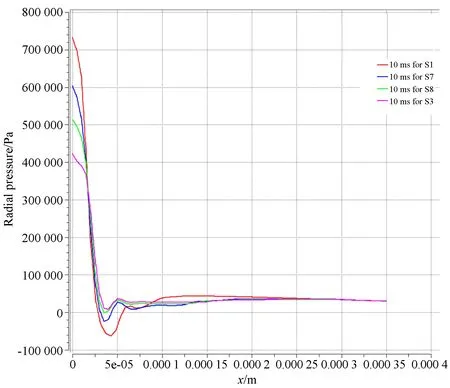
图6 仿真实验组二10 ms时刻气膜径向压力分布图Fig.6 Radial pressure distribution of gas film of comparison group 2 at 10 ms

图6是仿真实验组二气膜径向压力分布图，其分布规律类似，气膜中心是压力最高点，但深度的增加会导致峰值下降，然后沿径向先迅速下降，在扩散至均压腔后略有回升，最后平稳扩散至气膜边缘，无压力波动区域。相比无腔小孔节流结构在节流孔出口存在的负压区域，可以发现均压腔深度较低时，该负压区域仍存在，继续增加均压腔深度后消失。

4.3 均压腔直径对比仿真实验组三

图7为仿真实验组三的三维流线图，图8是对称面速度分布图。图7(a)和图8(a)环面节流的特征体现的非常明显，流体以上表面圆半径为节流孔半径的圆柱面为节流面，节流孔出口并没有向下扩散，和小孔节流形式区别明显，但在向气膜边缘的扩散中都处于层流状态，流场都比较稳定。

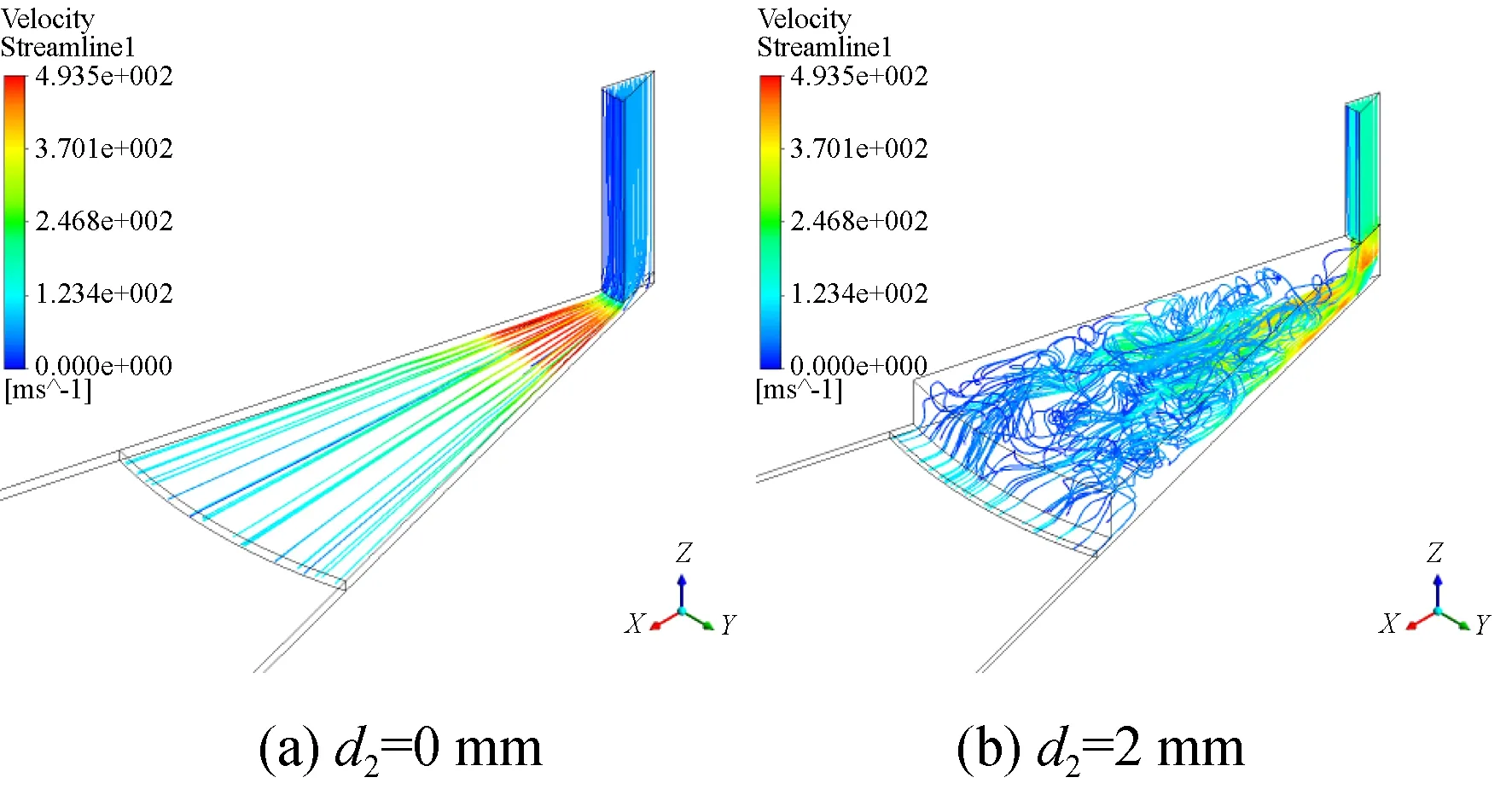
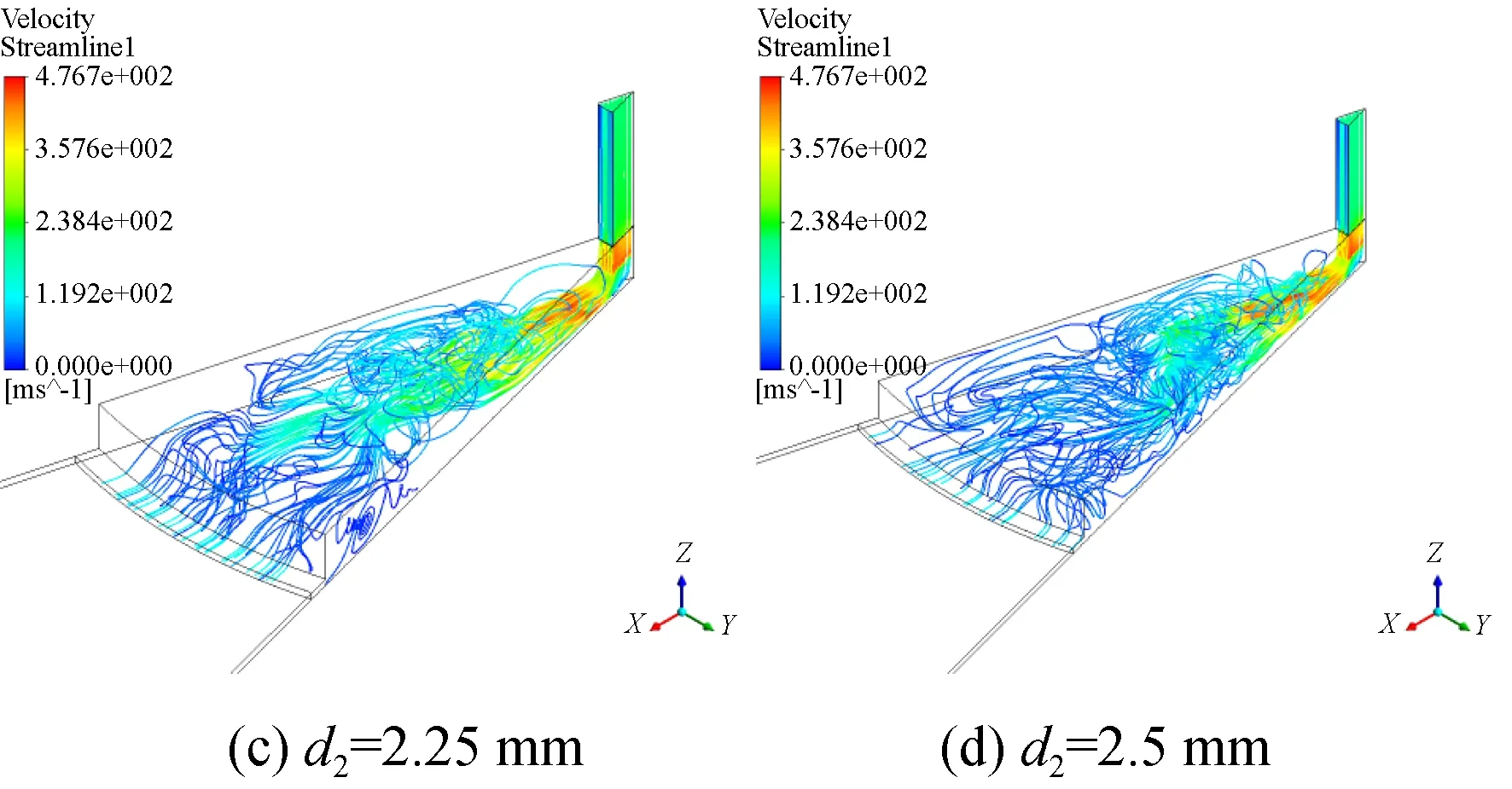
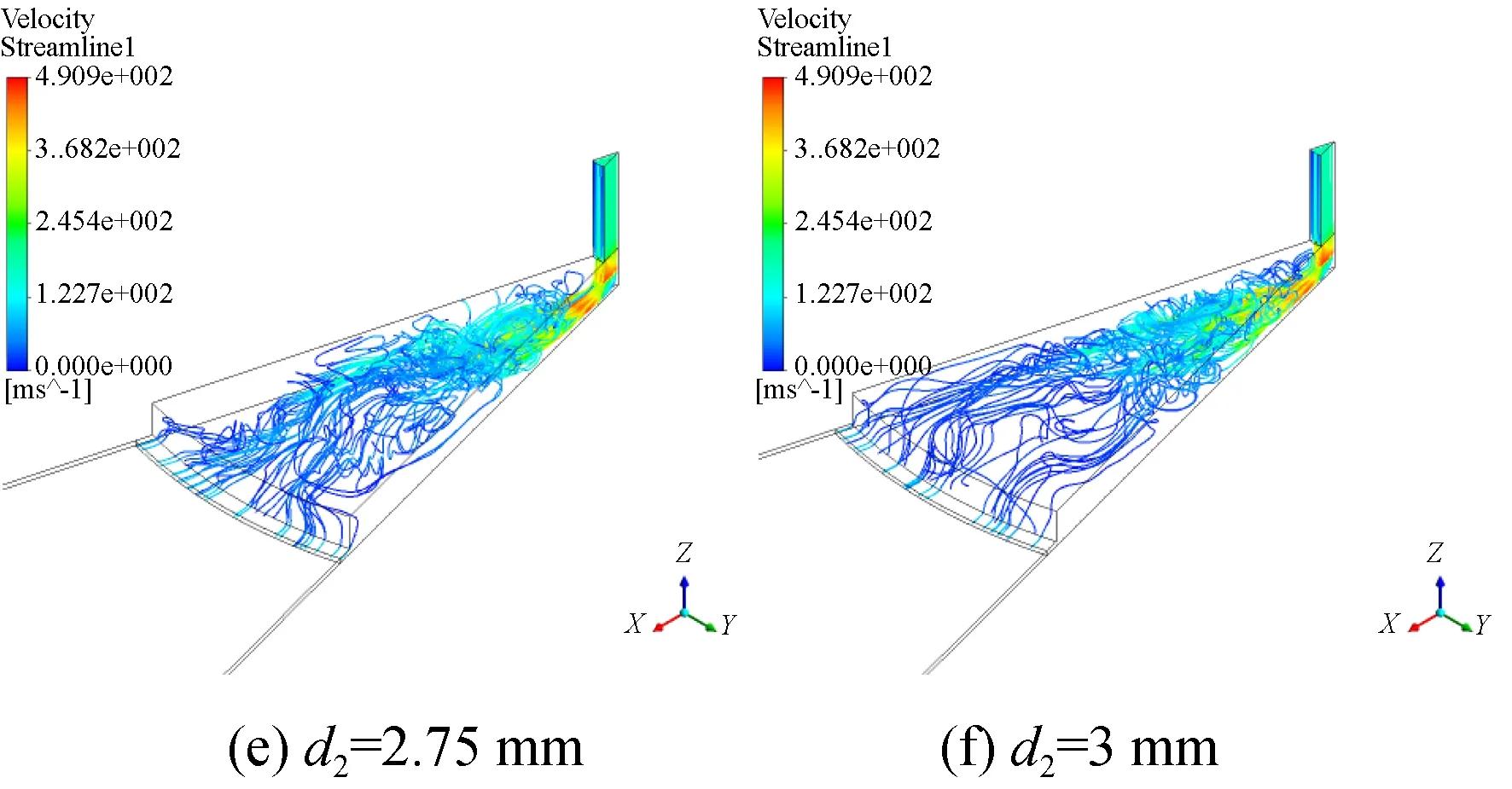
图7 仿真实验组三10 ms时刻三维流线图Fig.7 Three-dimensional flow diagram of comparison group 3 at 10 ms

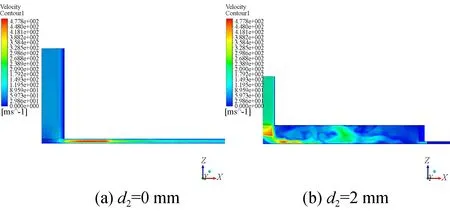
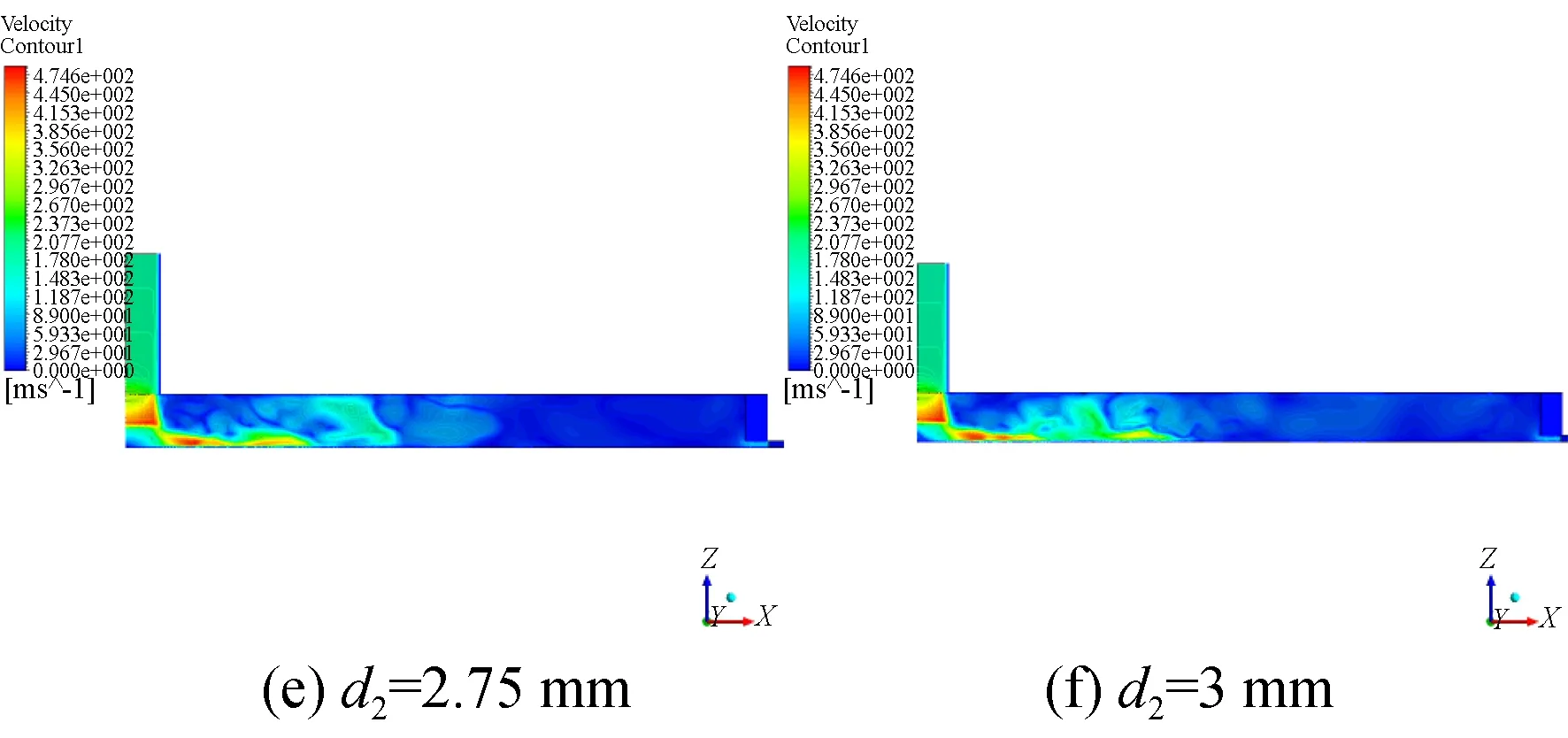
图8 仿真实验组三10 ms时刻对称面速度分布图Fig.8 Velocity profile of symmetric plane of comparison group 3 at 10 ms

观察实验组其他五个结构，可以发现当相对气容大于5%时，流体在进入均压腔后迅速变成复杂湍流，从节流孔出口至均压腔出口的涡结构开始呈现出复杂的三维特性，在极短时间内涡结构尺度和空间位置迅速且不规则发展，涡的破裂重组扩散都是极短时间内发生的，这也是湍流运动的一个显著特征，其流动方向也是不规则地迅速改变。

图9和图10是实验组三的涡量分布图，前者是大尺度涡，后者是小尺度涡。在保证均压腔内流体都变为湍流的结构中，随着直径的增加，变化最剧烈的地方一直是节流孔出口附近的区域，这一区域的流线密集而复杂，存在着迅速变化的大尺度涡结构，是气浮轴承微观流场最复杂的区域。然而主旋区并未随着直径的增加进一步扩散，只存在于节流孔出口附近。次级涡旋相比主涡旋，结构尺度偏小，且主要分布在均压腔出口附近。从流场的分布规律看，主旋区是气膜中最复杂，变化最快的区域，引发微振动的主要流区可能就是主旋区及周边区域。

图9 仿真实验组三10 ms时刻0.1 level涡量分布图Fig.9 0.1 level vorticity profile of comparison group 3 at 10 ms

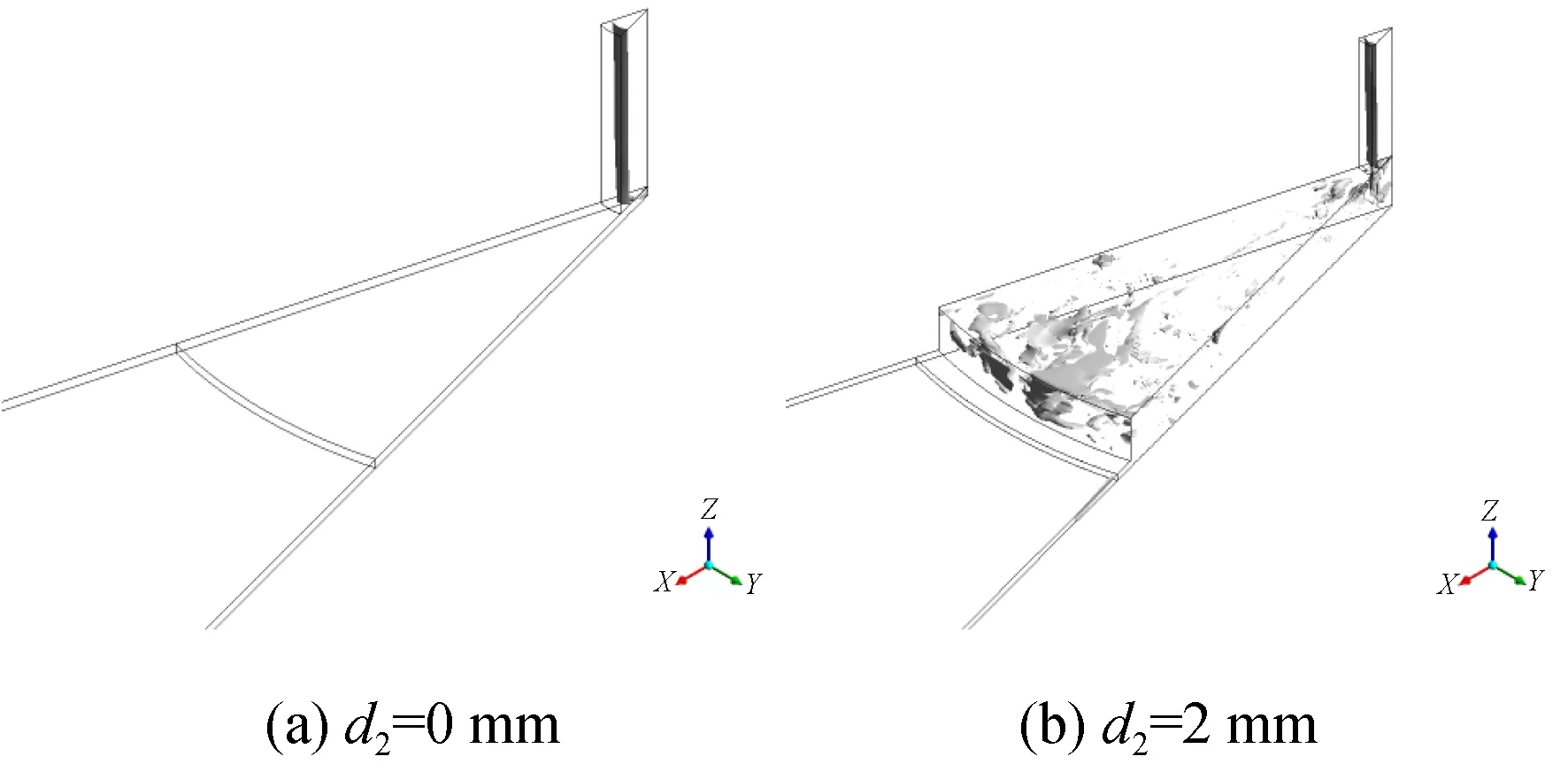
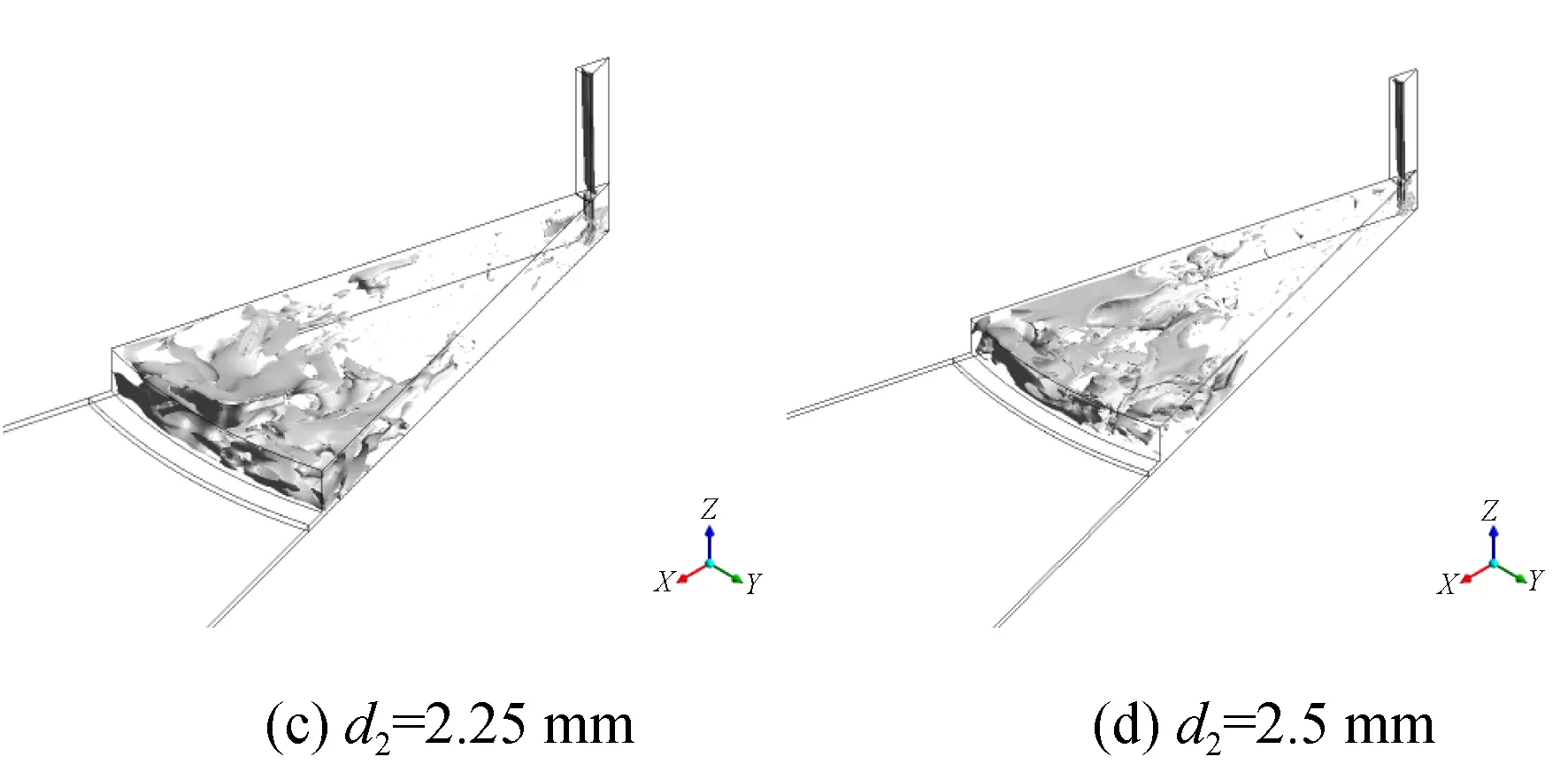
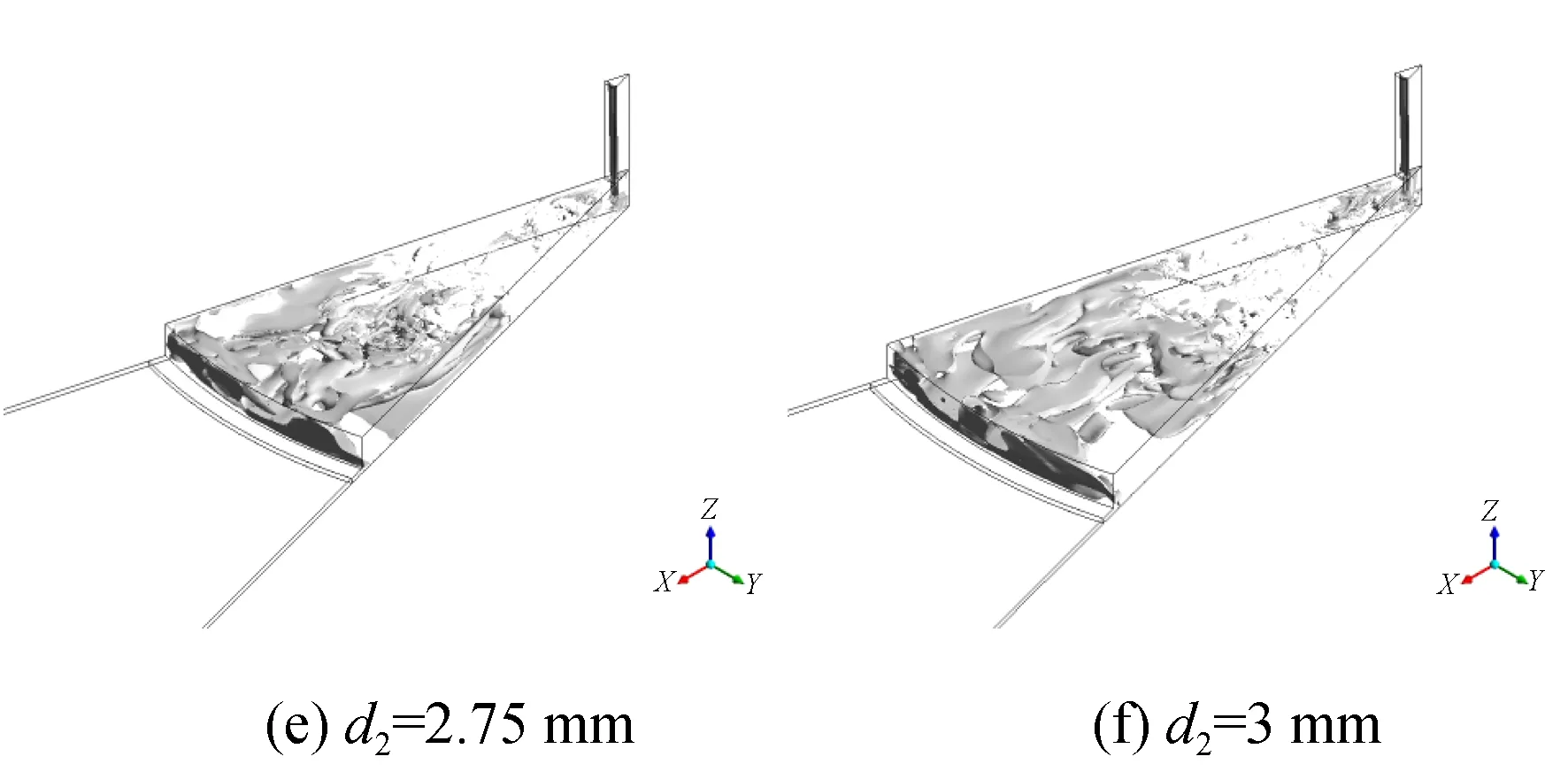
图10 仿真实验组三10 ms时刻0.01 level涡量分布图Fig.10 0.01 level vorticity profile of comparison group 3 at 10 ms

图11是气膜径向压力分布图，除了环面节流压力分布类似无腔小孔节流外，观察其余气膜表面径向压力分布，总体趋势一样，在均压腔区域靠近节流孔附近，产生一个区别于稳定层流的压力波动区，该区域压力剧烈变化；在均压腔出口还有一次压力下降，这是扩散至气膜区域产生的，变化程度远没有节流孔出口那么剧烈。相比上一组结构压力分布图，压力剧烈变化区的产生最为明显，所以认为正是节流孔出口附近的压力波动作为激励振源导致了轴在静态条件下的不稳定。

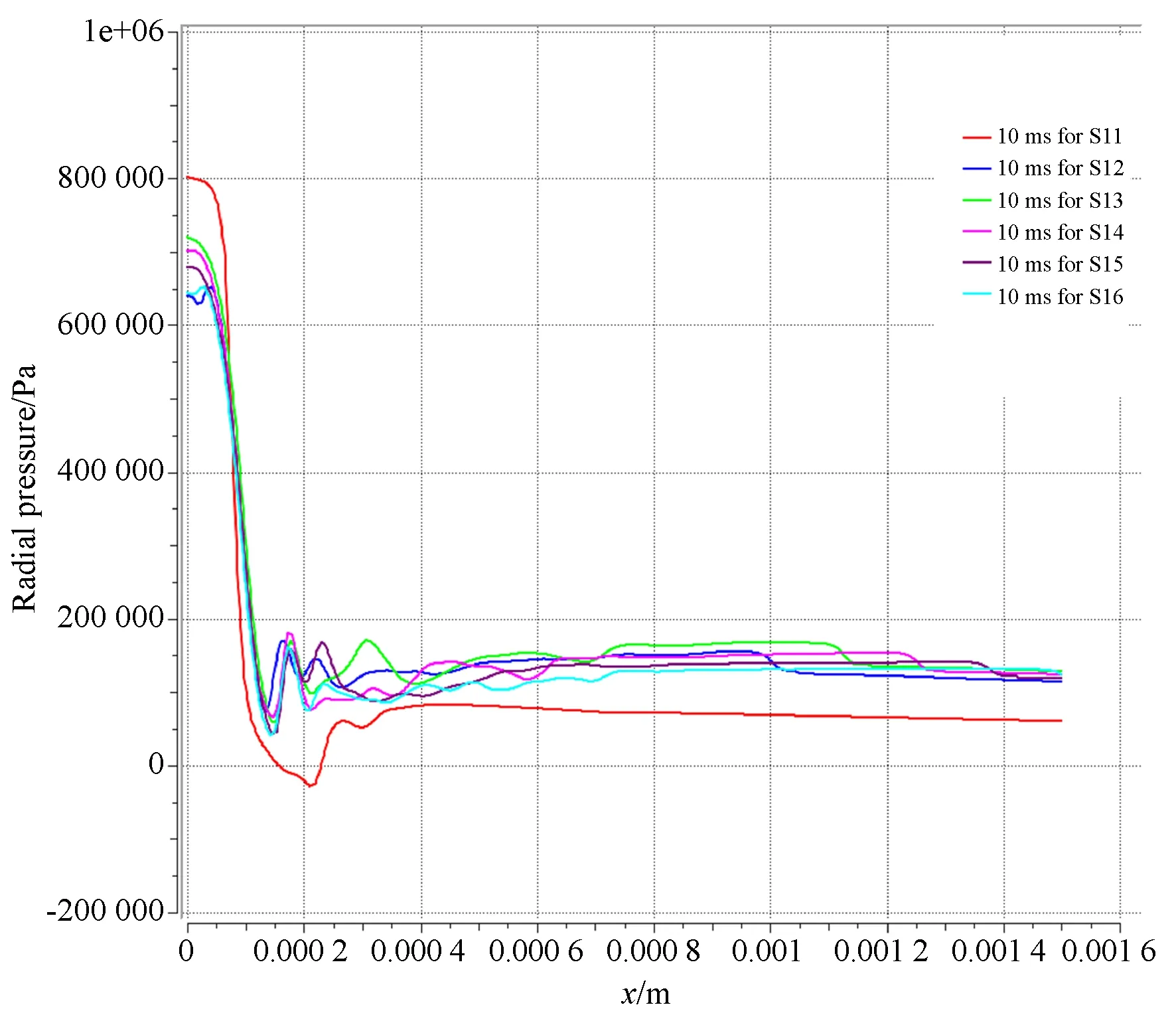
图11 仿真实验组三10 ms时刻气膜径向压力分布图Fig.11 Radial pressure distribution of gas film of comparison group 3 at 10 ms

在同等供气压力条件下，当气容比从6%向10%左右不断增加时，在压力波动最剧烈的区域，其波动压力范围和峰值也不断增加；在气容比继续增加至15%时，波动仍然剧烈，但整体压力范围和峰值随之下降；Z方向的压力梯度则随着气容比的增加一直增加，这种差异性与气流从小孔至气膜的压力突降程度有关，在一定区域内，压力变化更加剧烈，但是峰值略有下降。

4.4 均压腔高度对比仿真实验组四

以d2=3mm的结构为参照，不改变其它参数，只改变均压腔高度，相对气容从9%增至21%。图12为10 ms时刻三维流线图，图13为10 ms时刻对称面速度分布图，可以发现随着均压腔深度的增加，流场发展越充分，涡旋结构越明显，甚至扩散至整个均压腔区域，这是因为均压腔深度的增加会提供足够的空间让涡旋破裂重组。

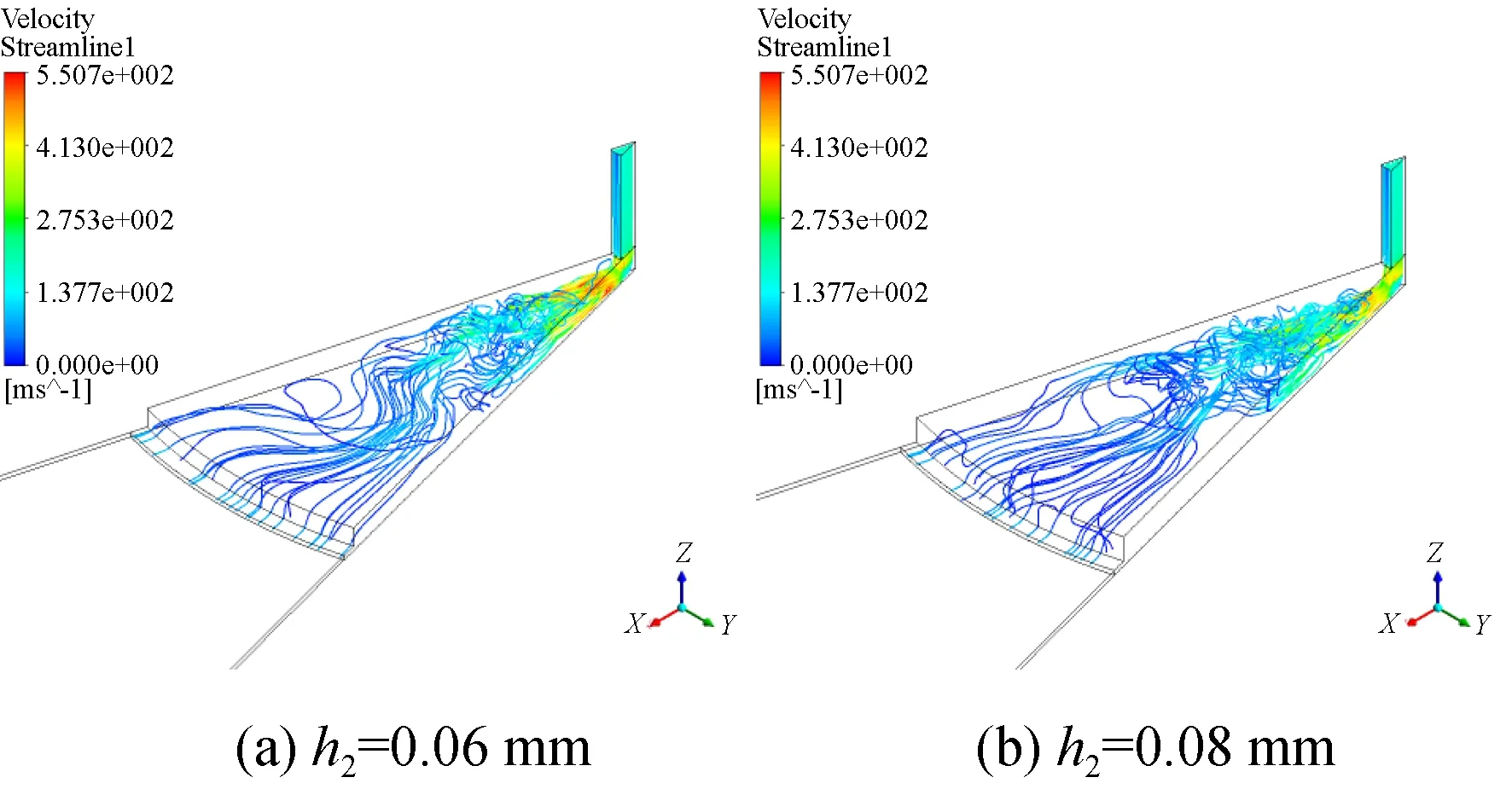
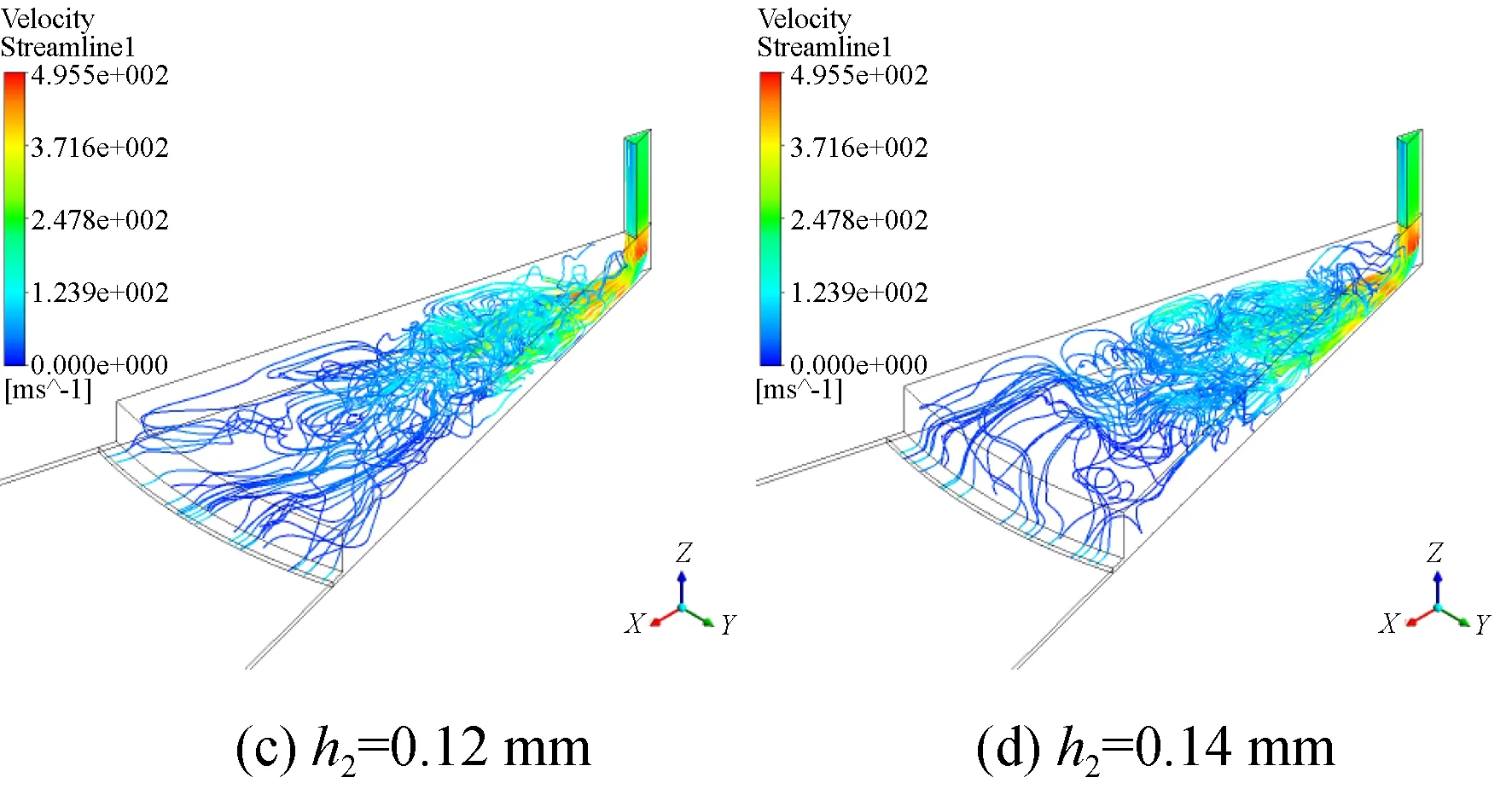
图12 仿真实验组四10 ms三维流线图Fig.12 Three-dimensional flow diagram of comparison group 4 at 10 ms

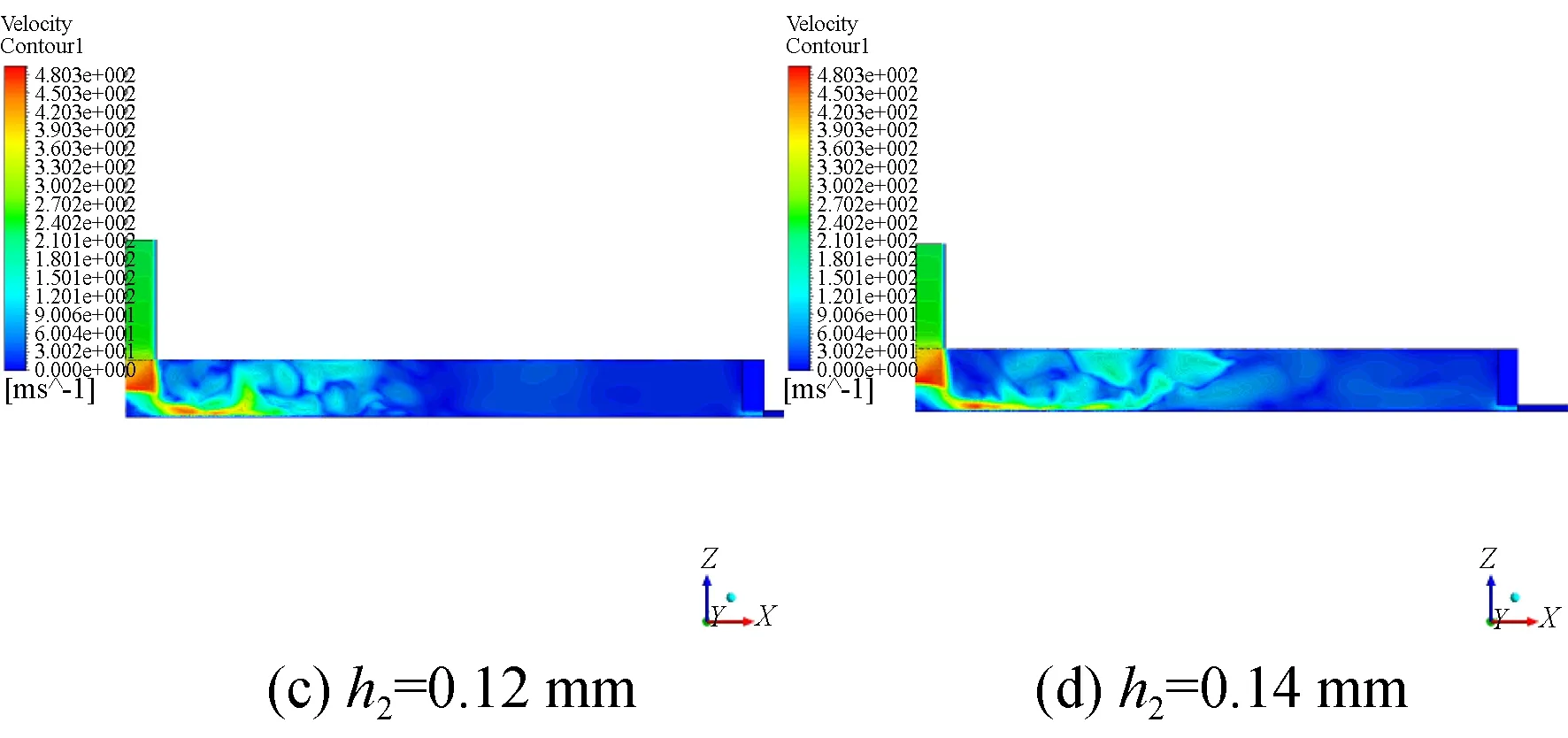
图13 仿真实验组四10 ms对称面速度分布图Fig.13 Velocity profile of symmetric plane of comparison group 4 at 10 ms

图14是10 ms时刻对比实验组四气膜径向压力分布图。均压腔深度较小时，负压现象仍然存在。随着均压腔深度的增加，压力波动范围和峰值都逐渐增加，而z方向压力梯度也是呈正相关关系，这再次说明一定程度的相对气容比会导致不稳定流场的充分发展，这也是不稳定性在微观领域的直观体现。

图14 仿真实验组四10ms时刻气膜径向压力分布图Fig.14 Radial pressure distribution of gas film of comparison group 4 at 10 ms

4.5 仿真实验组对比

(1)对比前4个仿真实验组结果，在气容比从0增至20%的过程中，微观流场整体发展趋势为简单层流逐渐过渡到复杂湍流，流场愈加不规则发展，而气旋的产生加剧了这一过程，涡旋分布有主旋区和次级涡旋且一直处于快速破碎重组的过程，再加上这一非稳区域的不断收缩和扩张，这一变化反应到宏观上就是微振动的出现和振动幅度的增加甚至发展成气锤振动。

(2)对比仿真实验组一和仿真实验组二以及仿真实验组三和仿真实验组四，可以发现改变均压腔深度在同等气容比范围内对流场影响更加剧烈，相对气容比在1%～5%以上的轴承气膜的流态会导致主轴系统的振动现象，且不同结构轴承临界相对气容比不同。

(3)对比仿真实验组一和仿真实验室三，可以发现在稳态和非稳流场下，改变均压腔直径对流场影响最直接的区域一直是均压腔出口附近，直径的持续增加并不会导致影响范围的明显扩张。

(4)对比仿真实验组二和仿真实验组四，可以发现在稳态和非稳流场下，改变均压腔深度在一定范围内对流场影响范围一直在均压腔内扩散，这一结论和上一结论有明显区别的原因在于涡旋发展需要一定的空间，而在同等相对气容比范围下改变均压腔深度更有利于流场的充分发展。

4.6 供气压力对比仿真实验组五

图15为气膜在1 ms时刻三维流线图，图16为1 ms时刻对称面速度分布图。可以明显发现，伴随着供气压力的逐步提升，流场在相同时间内变化的更为剧烈，主旋区也在逐渐向均压腔中心区域靠近，流场的不稳定性与压力变化呈现正相关。

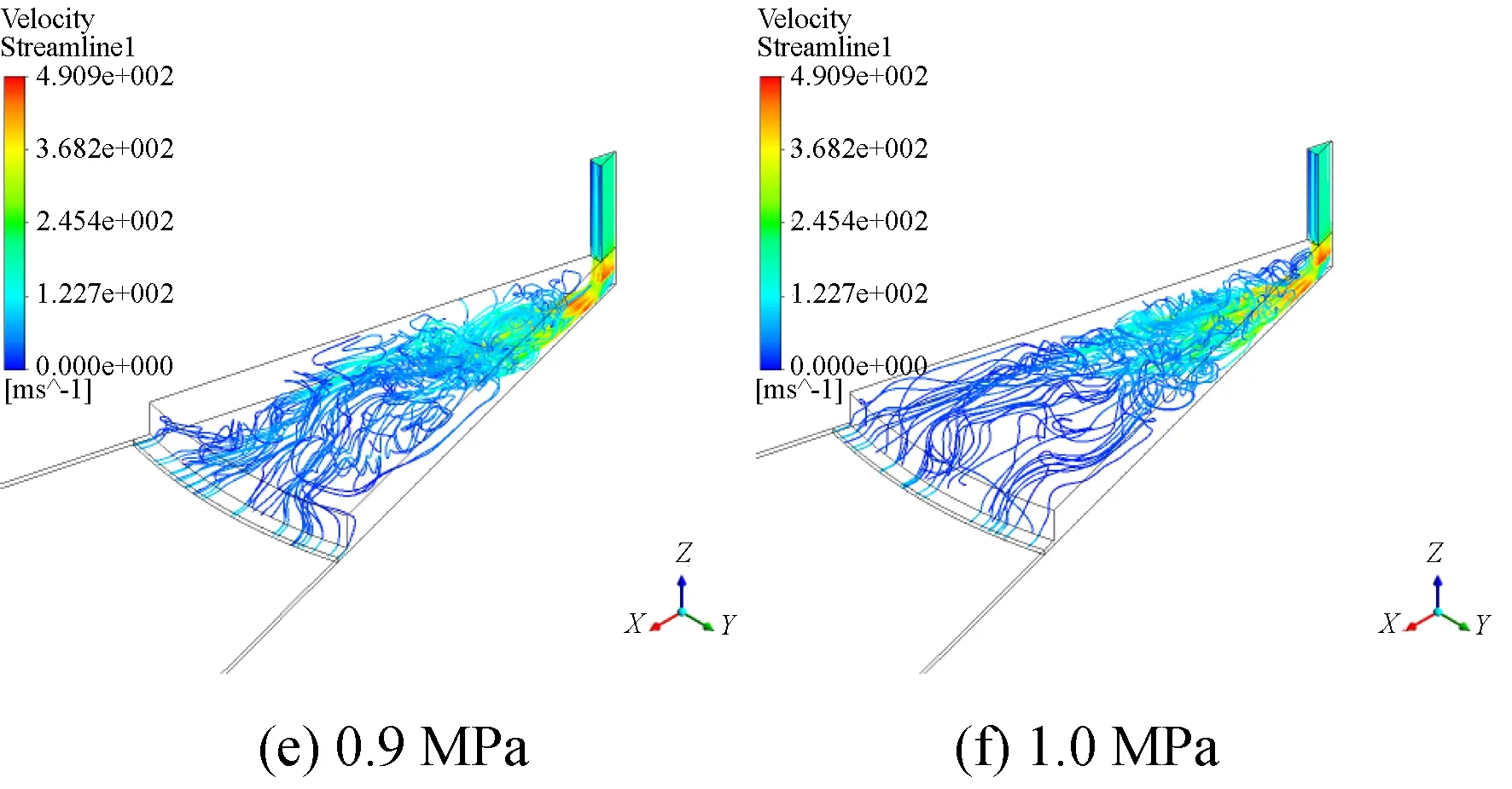
图15 仿真实验组五1ms三维流线图Fig.15 Three-dimensional flow diagram of comparison group 5 at 1 ms

图16 仿真实验组五1ms对称面速度分布图Fig.16 Velocity profile of symmetric plane of comparison group 5 at 1 ms

图17为1 ms时刻对比实验组五气膜径向压力分布图，随着供气压力的提升，气膜压力沿径向分布总体趋势变化一致，都是从小孔扩散至均压腔区域时有一个压力下降区，然后就是出现一个压力波动区，但是压力波动区域在逐渐远离节流孔出口。

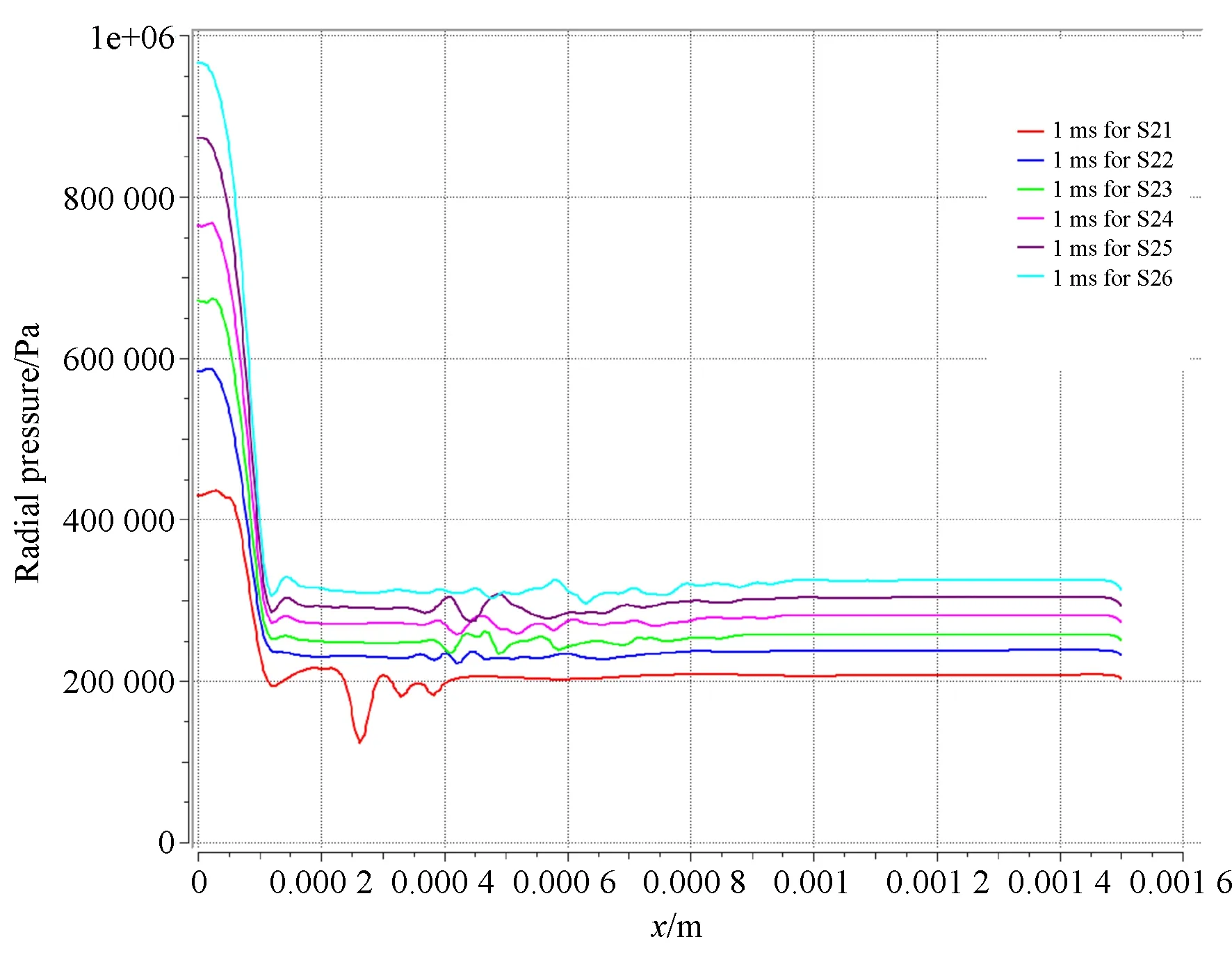
图17 仿真实验组五1 ms时刻气膜径向压力分布图Fig.17 Radial pressure distribution of gas film of comparison group 5 at 1 ms

5 实验测量与结果

小孔节流止推轴承静态特性测试实验平台如图18，静压主轴垂直放置在隔振实验平台上，在其上方放置三向加速度传感器，在气源系统正常工作下，通过数据采集装置测量气体静压轴承静态特性。如图19所示为0.4 MPa供气压力下测得主轴轴向运动数据，其最大位移为90 nm，验证了气体静压轴承在一定结构和压力下发生了微振动，其振动量级在纳米级。

图18 静态特性测试实验平台Fig.18 Experimental platform of static characteristic testing

表5 实验轴承关键参数

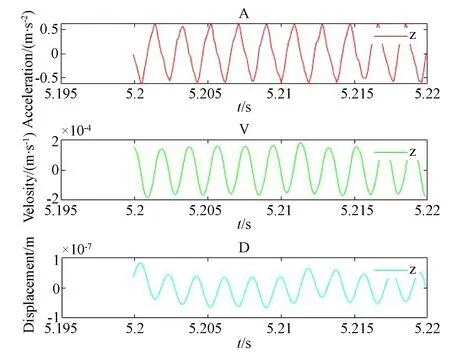
图19 主轴轴向运动测量值Fig.19 Measurement of spindle axial motion

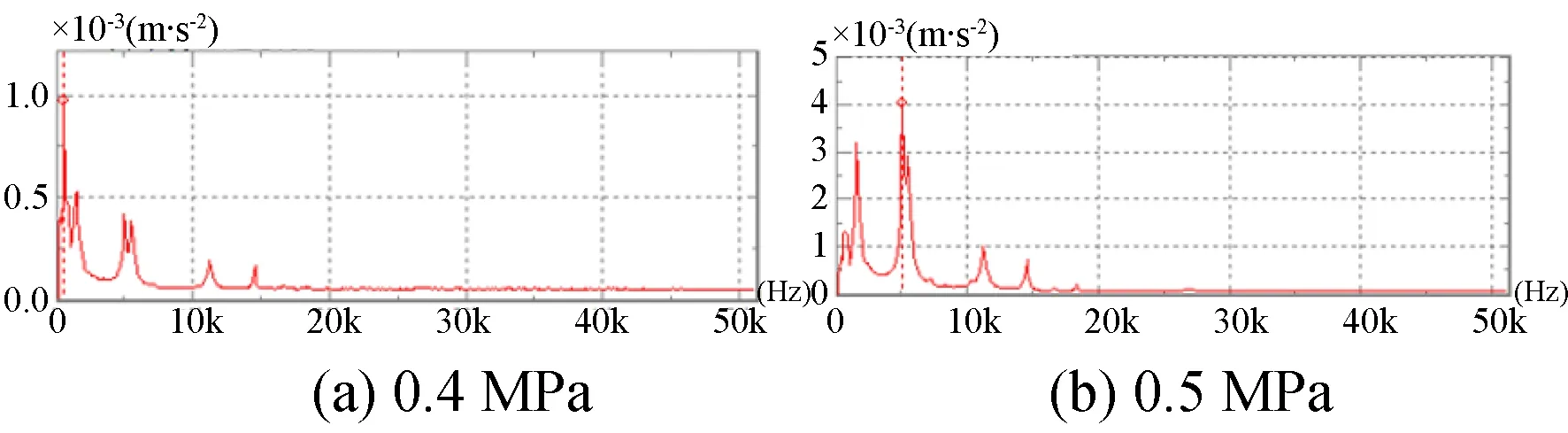
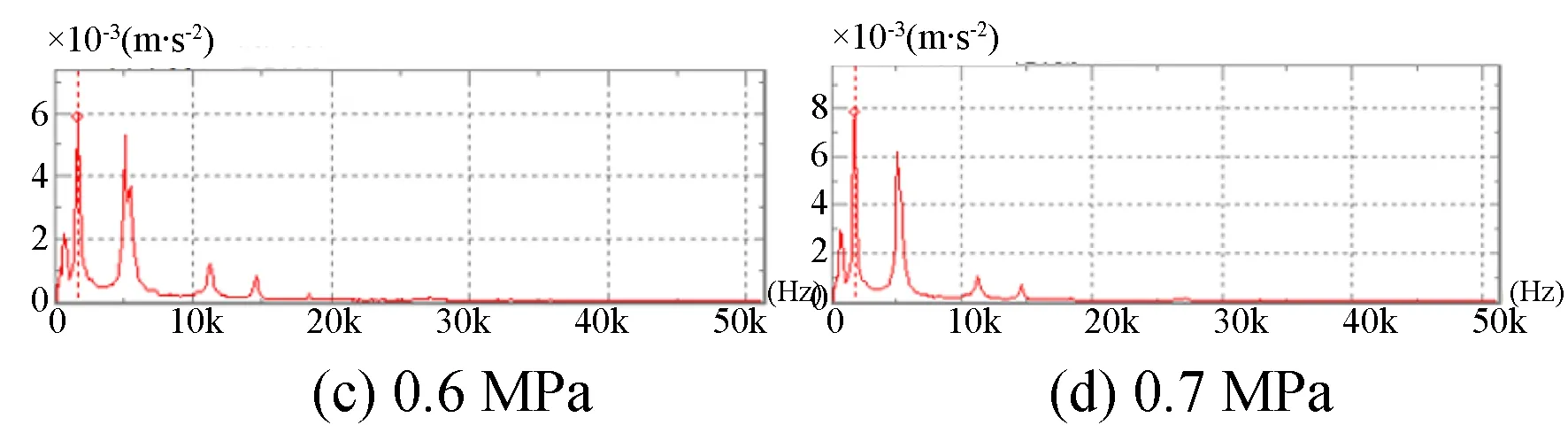
图20 加速度测量值Fig.20 Measurement of acceleration

如图21为仿真实验五气膜径向压力梯度仿真值，观察流场变化较为均匀的位置，选取0.1 mm位置的压力梯度，可以明显发现随着供气压力的提高，压力梯度也逐渐增加，由于加速度=压力梯度/密度，压力梯度和加速度呈正相关，也可以说加速度随着供气压力的提高而提高；取气膜径向上均压腔区域为测量区域，其上某点加速度在不同供气压力下的测量值如图20所示，供气压力0.4 MPa,0.5 MPa,0.6 MPa和0.7 MPa下的加速度峰值为1 m/s-2,4 m/s-2,6 m/s-2和8 m/s-2，可以发现随着供气压力的增高，加速度也逐渐增加，这一结论与仿真所得结论相符合，可以说LES仿真和实际在变化趋势上是吻合的。

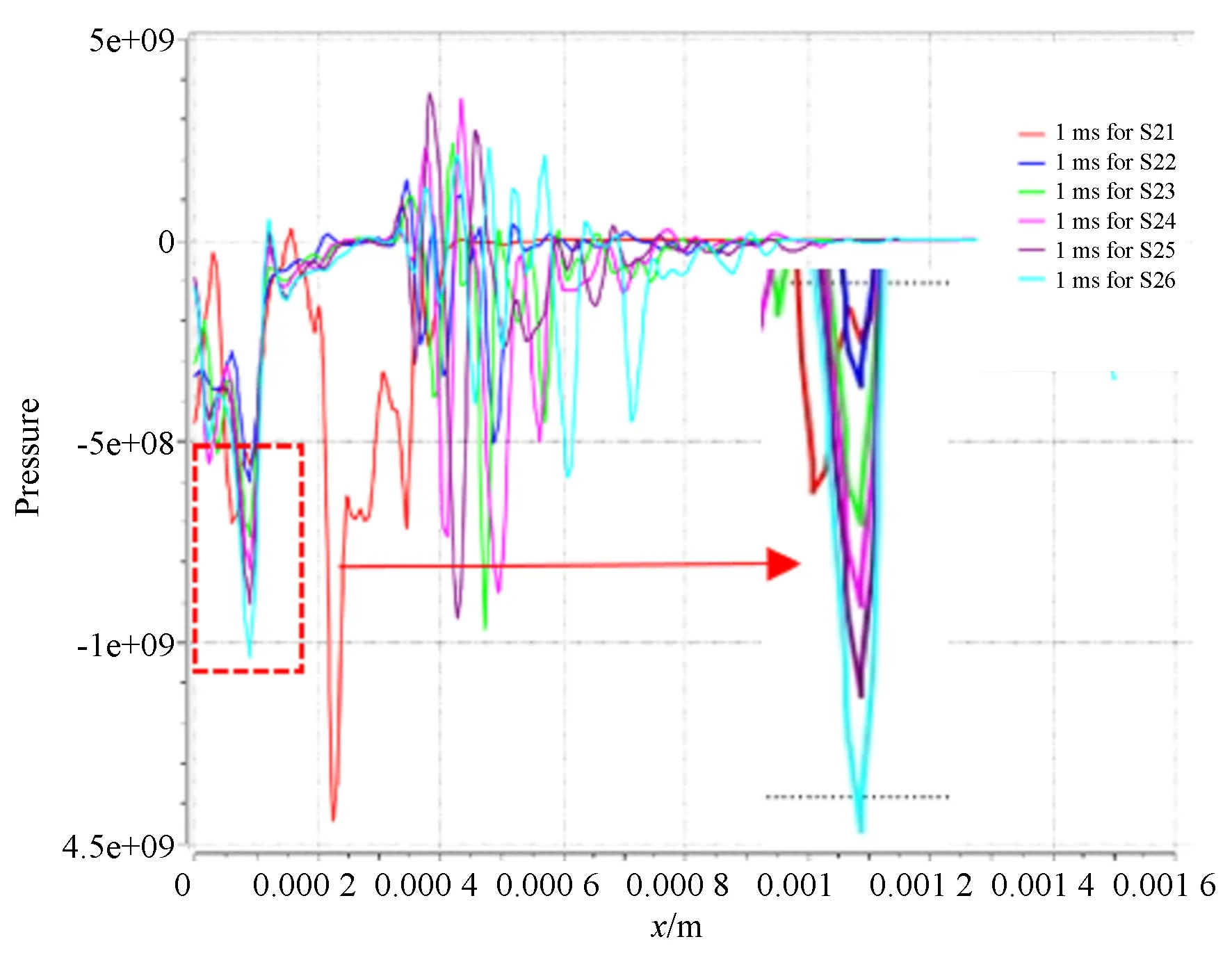
图21 气膜径向压力梯度仿真值Fig.21 Distribution of radial pressure gradient of gas film

6 结 论

本文通过建立具有中心进气孔的有腔小孔节流静压气体推力轴承模型，利用FLUENT计算软件进行LES仿真数值模拟计算，分析微观流场与微振动的关联，通过对计算结果分析可以得到如下结论：

(1)研究表面一定的内部气容是气体静压轴承微振动的必要因素。当相对气容在1%左右时，一定的内部气容就可能会导致气体静压轴承微振动。无腔结构下的微观流场整体处于层流状态，无明显涡旋，当相对气容比增加到一定程度，流场就以湍流流场为主导，流场的不规则发展和涡旋的复杂分布是微振动反应在微观流场的表现。

(2)均压腔的直径增加会加剧流场的发展，但增加到一定量时流场不会更进一步发展，流场变化最剧烈的区域一直在节流孔出口区域，并不会随着直径的增加进一步扩散，引发微振动的主流区可能是主旋区及周围流区。

(3)均压腔的深度增加同样会加剧流场发展，当深度接近气膜深度时，会有负压产生，随着深度的增加，流场充分发展，主旋区会随着深度的增加进一步扩散。

(4)相对气容比在5%以上的轴承气膜径向压力分布中存在压力剧烈波动区域，这一波动剧烈的压力作为激励振源可能诱发微振动发展为气锤振动。

(5)在供气压力逐渐提高的过程中，压力波动峰值逐渐增加，这也是主轴系统振动幅度随着供气压力增加而剧烈的原因。