一种基于斜向观测的镜面法线方向测量方法

杨再华，王子文，潘璐璐，孙 伟

（北京卫星环境工程研究所，北京 100094）

1 引 言

航天器总装集成时需要测量关键设备上光学基准镜镜面法线的方向，目前测量时需要将准直经纬仪放置在反射镜前方，通过精密位置调整，使经纬仪望远镜光轴与镜面准直。随着航天器结构日益复杂，常出现精测镜光路被遮挡的情况，因此项目组提出了一种基于斜向观测镜面法线方向的测量方法，在精测镜镜面斜前方架设一台经纬仪斜向观测反射镜中另外一台经纬仪反射来的平行光，再通过矢量计算得到镜面的法线方向。该方法源于平面镜成像原理，可以在反射镜正前方光路被遮挡的情况下实现镜面法线的测量。通过试验比对，该方法测量精度与准直方法测量精度差异在角秒量级，满足航天器测试要求。

2 测量原理

2.1 测量对象简介

航天器上设备基准经常为光学立方镜、平面镜等，如图1所示为星上某光电敏感器的立方镜基准，立方镜上3个互相正交的镜面法线代表其坐标系的坐标轴。航天器总装阶段，测量该敏感器坐标系相对航天器坐标系的姿态角度，实际上就是测量其立方镜镜面法线与航天器坐标系坐标轴的空间夹角。

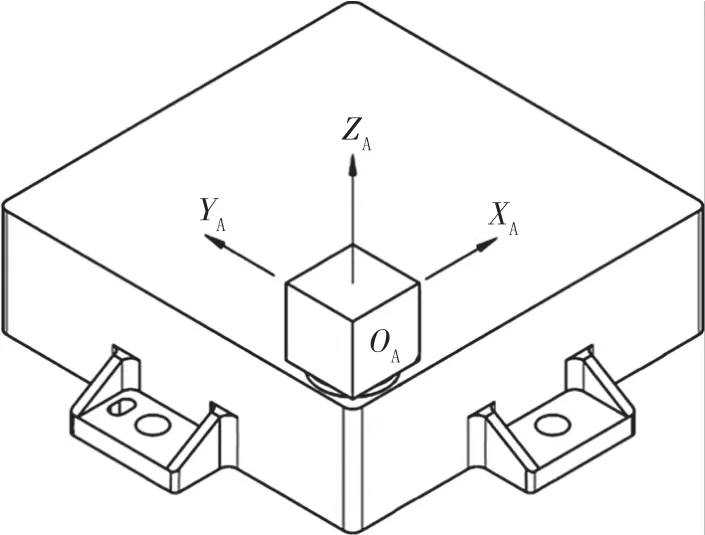
图1 带光学立方镜的星敏感器Fig.1 A star sensor with optical cube

2.2 经纬仪准直测量方法

当前航天器上设备基准测量主要使用准直经纬仪，如莱卡TM6100A。准直经纬仪是在普通经纬仪上加装了准直灯，当经纬仪物镜调焦到无穷远时，准直灯发出的点光源被望远镜扩为一束平行光。当平行光垂直入射到平面镜时沿原路返回，返回光经望远镜物镜汇聚于分划板中心。若准直光与被测镜面有夹角θ时，返回光则偏转2θ角度。设经纬仪望远镜焦距为f，则返回光汇聚点与分划板中心的距离d＝f×tan（2θ），如图2所示。

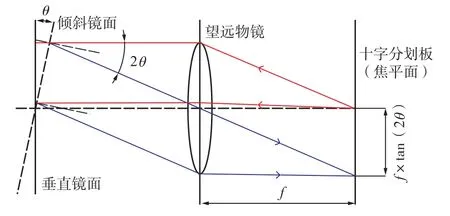
图2 镜面准直原理Fig.2 Principle of collimating plane mirror

使用经纬仪准直时，先通过支架将经纬仪概略放置于反射镜的准直光路上并调水平，再通过微调旋钮调节望远镜的方位角和天顶距，使返回光精确汇聚于分划板中心实现精确准直，此时记录下经纬仪的方位角H和天顶距V，方位角指经纬仪准直方向在水平面上投影与码盘0°方向的顺时针夹角，天顶距指准直方向与向上的铅锤方向夹角。如图3所示，架设经纬仪A准直被测立方镜A面，设得到经纬仪准直时方位角和天顶距为（H，V），以经纬仪码盘0°方向为X轴，铅锤向上为Z轴，由右手法则确定Y轴，则立方镜A面法线在经纬仪A坐标系下的矢量N按公式（1）计算

测量某被测镜面法线时，使用多台经纬仪建立测量网，通过经纬仪互瞄得到镜面法线在全局坐标系下的矢量。如图3所示，以经纬仪T坐标系OXYZ为全局参考坐标系，为了得到镜面A法线在全局坐标系下的矢量，将经纬仪T与A互瞄，设经纬仪T与A互瞄时的观测角分别为（H，V）、（H，V）。由于两经纬仪都经过精密调平和电子水平补偿，计算时忽略水平误差，两经纬仪坐标系间关系可以简化为围绕Z轴旋转一定角度θ，按公式（2）计算

图3 经纬仪准直互瞄测量原理Fig.3 Measurement principle based on theodolite collimation and bucking

则镜面法线A在全局坐标系下的矢量N按公式（3）计算

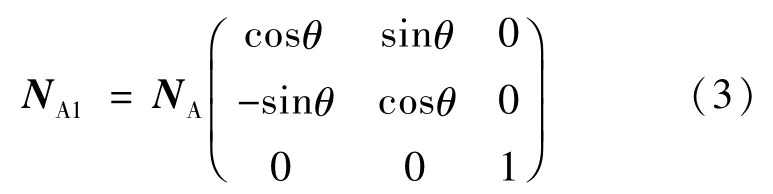
2.3 斜向观测镜面法线方法

针对被测镜面准直方向被遮挡的情况，本项目基于平面镜成像原理提出了一种斜向观测方法。如图4所示，某被测镜面正前方有障碍物，无法架设准直经纬仪由正前方观测，因此，架设经纬仪B斜向观测被测镜面并调焦到无穷远，经纬仪B望远镜投射出的平行光束被平面镜反射，在其反射光束方向架设经纬仪C，精确调整C的位置和朝向使来自经纬仪B的平行光束经过经纬仪C的望远物镜汇聚于其焦平面中心。通过两台经纬仪进一步精密微调，使经纬仪C发出的平行光经反射后汇聚于经纬仪B的焦平面中心，此时记录经纬仪B与经纬仪C的观测角（H，V）、（H，V），将其分别带入公式（1），得到在经纬仪B和C坐标系下的观测矢量N、N。

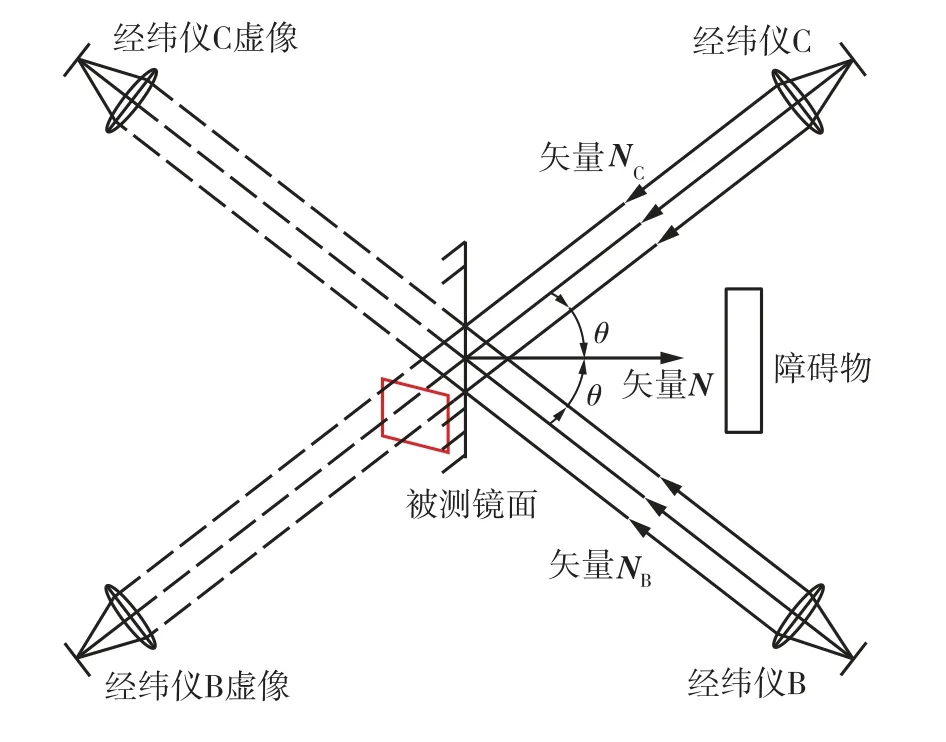
图4 斜向观测法线原理Fig.4 Principle of oblique observation with two theodolites

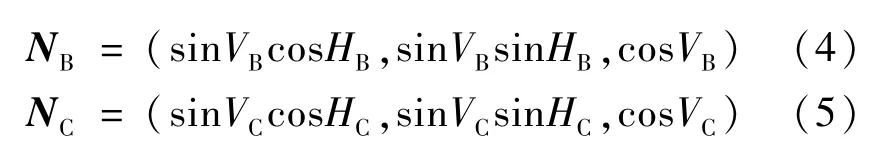
架设经纬仪T作为全局基准，将经纬仪B与经纬仪C分别与T互瞄，得到互瞄方位角分别为H、H、H、H，根据公式（2）和公式（3）将图4中经纬仪B和C坐标系下的观测矢量N、N转换到经纬仪T坐标系下得到矢量N、N。

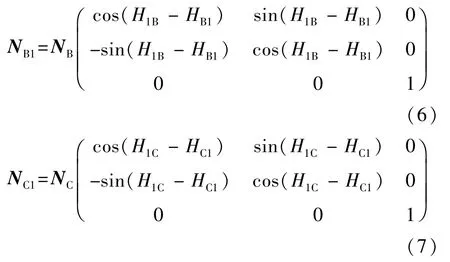
则平面镜镜面法线在全局坐标系下的归一化矢量N按公式（8）计算，原理如图5所示。

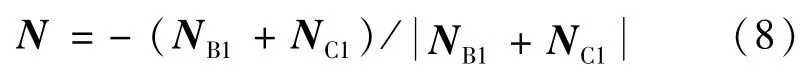
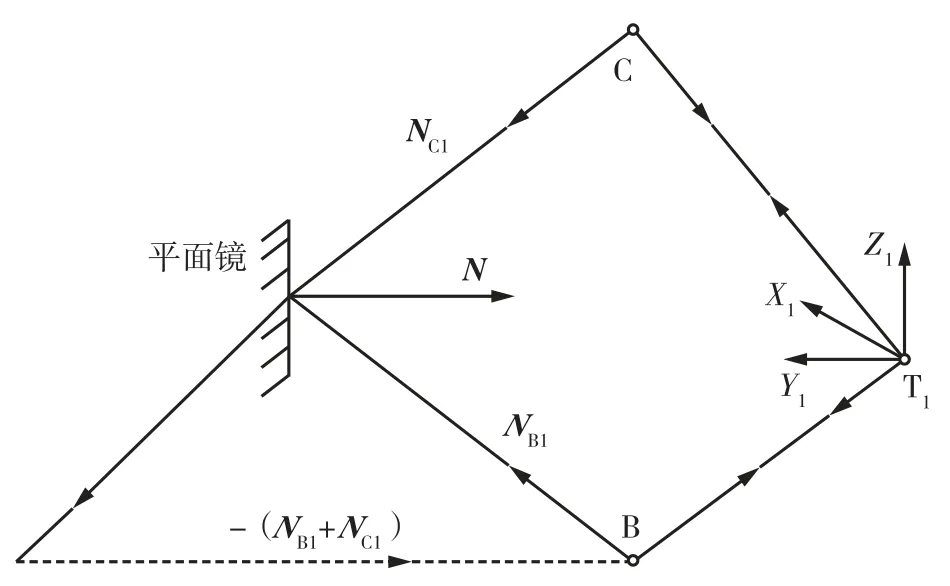
图5 矢量计算原理Fig.5 Principle of vector calculation

3 试验验证

根据第2章中提出的测量方法，搭建了试验系统如图6所示。架设一台莱卡经纬仪作为全局基准T，架设经纬仪A直接准直被测立方镜反射面，再与经纬仪T互瞄，直接测量镜面法线在全局基准坐标系下的矢量。架设经纬仪B，斜向瞄准立方镜反射面上十字线中心，然后将物镜调焦到无穷远并打开准直灯。保持经纬仪B不动，架设经纬仪C在另一侧，斜向瞄准反射镜十字线中心，进一步调整经纬仪的位置，使其观测到经纬仪B的反射光，并使反射光精确聚焦于分划板中心。将经纬仪C物镜调焦到无穷远，此时经纬仪C的平行光也应聚焦于经纬仪B的分划板中心。通过反复精确调整，最终完成斜向观测。试验中进行了多次重复测量，其中一组观测数据见表1，计算结果见表2，准直测量与斜向观测差异0.001 8°，即6″。

图6 测量试验现场Fig.6 Experiment with theodolite measurement

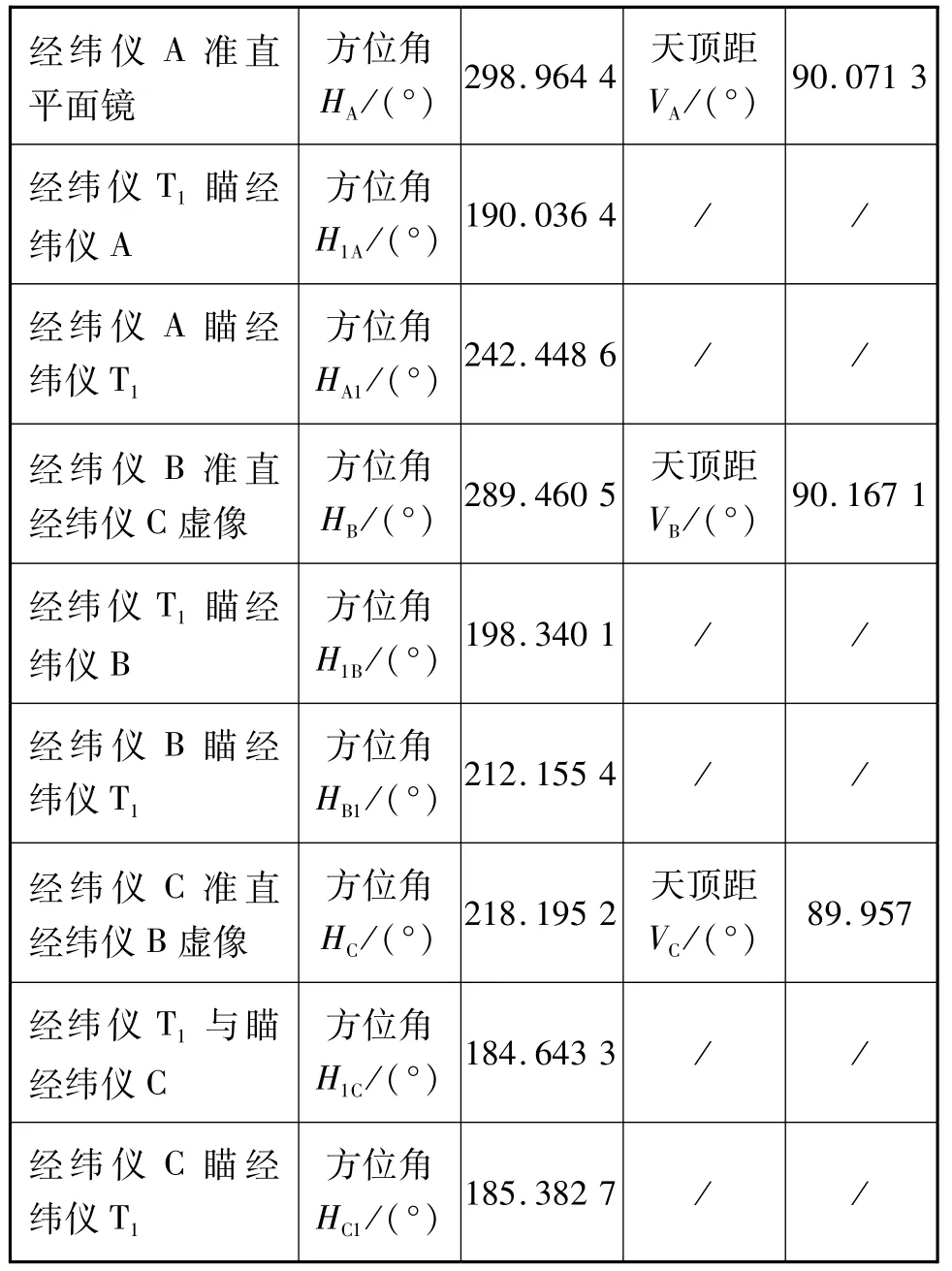
表1 观测数据Tab.1 Observed data

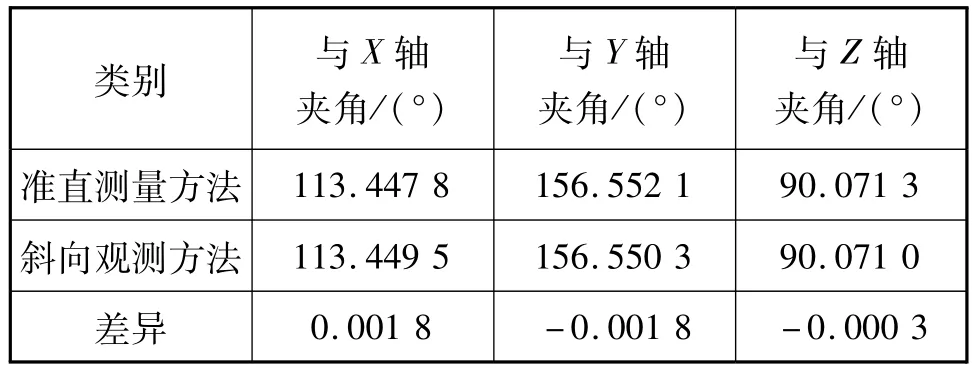
表2 计算结果Tab.2 Calculation result

4 结束语

本文针对航天器上光学基准镜准直光路被遮挡时镜面法线无法测量的问题，提出了一种基于两台经纬仪斜向观测的镜面法线测量方法。通过试验比对，该方法与经纬仪准直测量精度相当，差异在角秒量级，可以满足航天器测试需求。使用该方法不仅可以解决某些光学立方镜侧面被遮挡时无法测量的问题，还可以将两台经纬仪架设在高处从斜向测量立方镜的顶面法线，在航天器总装测试阶段有广泛的应用前景。