筒形铝合金件半固态触变成形过程有限元分析

牛海侠，张 琼

筒形铝合金件半固态触变成形过程有限元分析

牛海侠，张 琼

（安徽三联学院 机械工程学院，安徽 合肥 230601）

以圆筒形A357铝合金件为研究对象，通过创建几何模型、物理模型和有限元模型，运用DEFORM有限元仿真分析软件，对其半固态触变成形过程进行了有限元分析与模拟，获得在不同变形条件下的密度，并从中发现了其变化规律，为铝合金半固态触变成形的研究提供技术支持。

半固态触变成形；铝合金；有限元分析；DEFORM

半固态金属成形技术相比传统热加工和塑性变形具有很多优势。经过多年的研究和发展，铝合金半固态成形技术已在汽车零件制造业中得到广泛应用[1]。目前国内外学者对不同类铝合金半固态坯料的制备方法进行了大量研究[2-4]，并在常用的重熔再结晶方法（RAP）和应变诱导熔体激活（SIMA）法的基础上提出了新型的坯料制备方法[2-7]。

半固态成形技术充分利用金属材料在半固态温度区间特殊的微观组织和成形性能，能够在较低的成形载荷下实现复杂构件的高效近净成形，该技术的应用对于提高金属材料的利用率、延长模具的寿命以及实现绿色加工和节能减排等方面具有重要的作用[8]。

研究铝合金半固态坯料在感应加热过程中的组织演变规律，并实现复杂构件近净成形，对圆筒形铝合金件的半固态触变成形过程进行有限元分析与模拟，能够更直观和深入研究铝合金半固态触变成形的变形过程，帮助研究人员进一步优化模具设计相关参数，制定生产过程中的工艺参数，更好地把握产品的质量和性能，以及更好地了解各参数间的相互影响规律。因此，半固态成形的有限元分析与模拟尤为重要。

实际的半固态加工变形包含非常复杂的变化过程，主要是热力耦合的刚-粘塑性变形过程。在半固态的触变成形过程中，和塑性变形量相比较，弹性变形量非常小，可以忽略不计。在本文中把铝合金A357看成是刚-粘塑性有限元模型。DEFORM有限元仿真分析软件提供了145种材料的流动应力模型。本文采用的流动应力模型的形式是：

这个应力应变模型需要以表格的形式输入，并且，应力应变数据需要在实验中测量，以获得A357铝合金材料在不同的温度和应变速率下的应力——应变关系。

本文通过等温压缩实验，分别测得A357铝合金在568、574、580℃的温度下，在不同的应变速率下的真应力——真应变关系曲线来创建A357的流动应力模型。将测得的数据输入到软件的前处理系统，并运用log-log空间线性差值分析方法构建材料的流动应力模型。

1 几何模型的建立

运用UG三维造型软件，创建模具和坯料的实体模型。本设计是为了分析材料在模具中的变形和流动情况，因此，只设计了凸模和凹模的实体模型。设计完成，将零件保存为stl格式。下一步，将三维模型导入DEFORM软件，通过前置处理器输入接口得到三维实体模型，将坯料模型划分网格，在筒壁和底部连接处增加网格数量，以便在受力分析过程中能够得到更精准的数据。在整个有限元触变模拟中，由于凸模、凹模的受力变形比较小，不考虑凸模和凹模的受力和变形变化。因此，把凸模、凹模定义为刚体，把坯料定义为多孔材料的伪塑性体。这样，在DEFORM软件中，就把坯料、凸模、凹模的几何模型创建成功。

接下来，要定义坯料、凸模、凹模之间的空间位置关系以及运动方式。根据设计，将凸模定义为主动件，在机床滑块的带动下能够上下运动，实现对坯料的挤压成形。由于凹模装配在机床的工作台上，因此，将其定义为静止不动。坯料作为从动件，在凸模和凹模的共同作用下实现被动运动。本模拟中，定义的坯料、凸模和凹模都是轴对称零件。

通过DEFORM软件主要模拟了坯料触变成形过程中相对密度的变化情况，然后分析研判，得到筒形件触变成形中的密度变化规律，并为筒形件密度不均匀的问题提供解决方案。

2 物理模型的建立

模拟中所需要的物理模型主要包括坯料的材料性能、触变成形温度、凸模与凹模和坯料之间的摩擦系数等相关参数。半固态A357铝合金的材料的性能问题是定义其本构方程。半固态成形的模拟结果是否精准，主要取决于材料的本构方程能否正确地描述材料在半固态下的变形行为。其方程如下：

薄守生、董照辉（2007）在考察了生态语言学的一些研究之后,从语言多样化、濒危语言、国家发展模式、普通话推广、不可知论等五个方面进行了论述。金志茹等（2009）综合国内网络语言的发展现状，分析国外关于网络语言的政策和措施,提出对待网络语言的规范化问题。沈艺虹（2004）、孙辉（2010）从网络语言规范化角度对相关语言政策进行了论述。

（1）微分平衡方程或运动方程

（2）速度和应变速率关系(协调方程)

（3）应力-应变速率关系

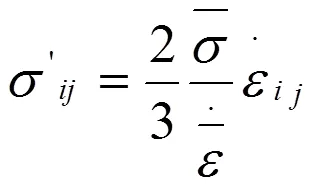
（4）屈服准则

（5）体积不可压缩条件

（6）边界条件

在力面S上：

在速度面S上：

要准确地模拟A357铝合金的半固态触变行为，还需要创建合理的摩擦模型。金属在半固态下变形，应变量比较大，变形温度也高，相对来说，材料的摩擦力比较大，屈服力相对较小。凸模、凹模和坯料之间的摩擦关系采用剪切摩擦，其模型如下：

式中：为剪切应力；为剪切屈服强度。

在DEFORM的前处理器中建立几何模型和物理模型后，通过设定各项控制参数后就可以利用求解器进行计算求解。求解过程中，DEFORM可以自动进行网格重划，以优化参数，得到更加精确的解。求解结束后，用后处理器导出结果，进行分析和判断。

3 有限元网格划分

考虑半固态铝合金A357的材料性能和模拟分析要求，将材料的初始密度定义为0.960；模具与坯料之间的摩擦系数定义为0.4；应用Absolute法划分网格，单元体的最小尺寸为1.3 mm；尺寸比为3，单元体的个数为18 692，步数为450步，步长为0.1 mm。

有限元模拟的触变成形过程中，网格的变化情况如图1所示。由图可以看出，在模拟的过程中，出现了网格细化的情况，这是因为在DEFORM的前处理器中，设置了局部网格细化，系统将自动重画网格，在变形复杂的地方网格比较密，这样就提高了模拟结果的精确度。

图1 触变过程中的网格变化

4 模拟结果与分析

4.1 触变成形过程中的相对密度变化

流体力学中所谓的不可压缩通常指流体的密度是恒定的。然而在半固态凝固过程中，液固相密度还是有微小的差异的。半固态时，密度随着温度的变化而变化，亦会随着凝固过程中的压力的大小而产生差异，如图2所示。因此，在有温度梯度下的流动不完全是恒密度流动。导热系数、比热容、密度等都是当地温度的函数，这是因为凝固区内的介质既非单纯的液相介质，又非单纯的固相介质，可以认为凝固区内的密度随温度是线性变化的[9]：

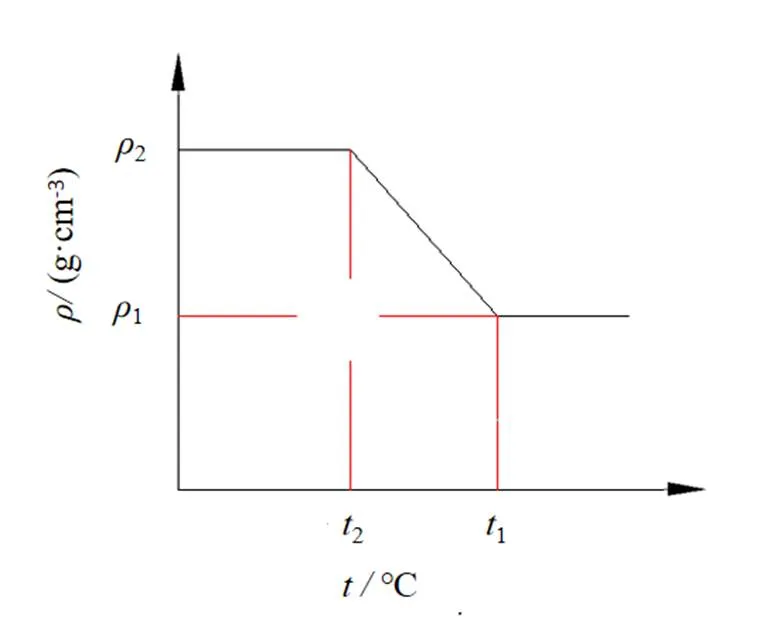
图2 密度随温度的变化趋势

根据上述原理，研究了半固态触变成形过程中相对密度的变化情况：

（1）压力恒定为100 MPa时，坯料的高度分别为35、40、45、50、60 mm，得到的相对密度的变化如图3所示。

由图3可以看出：压力增大，坯料各处的相对密度都增加，且在触变成形初期增加的最快；随着压力的不断增加，1、3点区域的相对密度增加比较快，在很短的时间就达到几乎稳定的状态；而2点增加的比较缓慢。但是随着压力的增加，此点的相对密度最后超过1点，几乎和3点相同；随着坯料高度的增加，2点的相对密度增加的越来越缓慢。可见，增加坯料的高度，对2点的影响比较大，使其相对密度越来越小，成形件的致密性越来越差。

（2）坯料的高度35 mm时，压力分别为60、80、100、120、140 MPa，得到的相对密度的变化如图4所示。

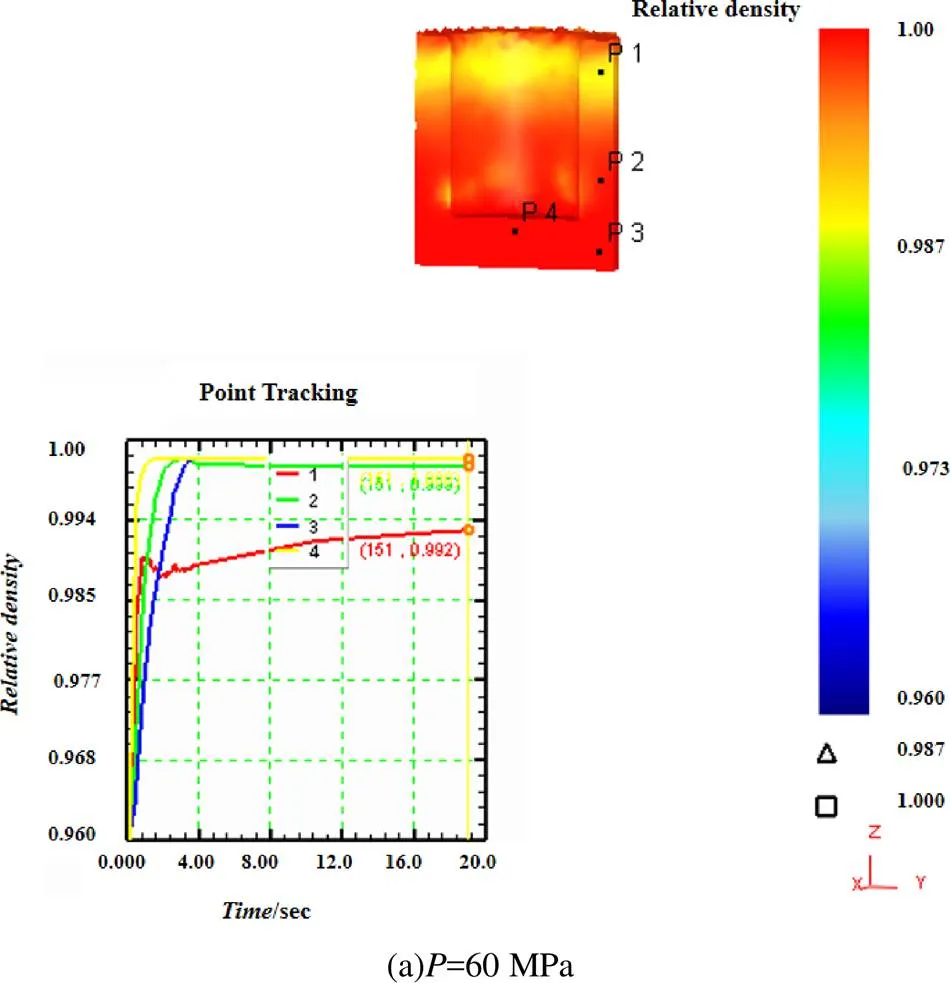
由上组图看出：施加的压力增加，筒各处的相对密度都有所增加。并且在很短的时间内，2、3、4点处的相对密度达到了最大值。在随后的触变成形过程中，变化不再明显；1的相对密度也是随着压力的增加逐渐增大，但是整体的变化过程比较缓慢，还有一定的保持阶段，在触变成形结束后，此处的相对密度仍低于其它点的值；2、3、4点区域的最大相对密度在很小的压力下(120 MPa)就达到0.999，而对1点来说，即使压力增大（140 MPa），最大相对密度值也仅从0.987增大到0.998；在半固态触变成形筒形件时，需要适当增大压力以使侧壁与底部的相对密度一致；模具施加压力的大小对筒形件侧壁的相对密度影响较大。因此，对触变成形件的性能也有较大的影响。为使筒形件的筒壁与底部有相同的性能，需要采用局部加载的方式以获得较好的成形效果。

4.2 筒形件筒壁与底部密度差的减小

通过以上的模拟结果可以看出，筒形件的筒壁与底部之间存在相对密度的差异，为了减小这些差异，使零件相对密度一致，筒壁的相对密度值增大，采用局部加载的方式将会很好地解决这一问题。其示意图如图5所示。

图5 触变模锻局部加载示意图

图6是数值模拟的结果，可以看出采用局部加载后筒壁的相对密度值几乎达到1.000，整个成形件的密度比较均匀一致。因此，数值模拟证实：采用局部加载这一措施可以减小密度差异。本方法正确、可行。

图6 局部加载后数值模拟的相对密度值

5 结论

通过有限元模拟半固态A357铝合金筒形件的触变成形过程，得出其相对密度的变化规律：筒形件的筒壁与底部之间存在相对密度的差异。为了减少密度差异，增大筒壁的相对密度值使零件相对密度一致，采用局部加载的方式解决了这一问题。

[1] 孟毅. 半固态成形工艺特点及发展现状[J]. 精密成形工程, 2016, 8(4):21-27.

[2] IANG J F, WANG Y, QU J. Effect of Process Parameters on Microstructure and Properties of AM50A Magnesium Alloy Parts Formed by Double Control Forming[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(2): 321-333.

[3] NEAGA Adriana, FAVIERB Veronique, BIGOTC Regis, et al. Microstructure and Flow Behaviour During Back[1]ward Extrusion of Semi-solid 7075 Aluminum Alloy[J]. Materials Processing Technology, 2012, 212: 1472-1480.

[4] BOLOURI A, SHAHMIRI M, KANG C G. Study on the Effects of the Compression Ratio and Mushy Zone Heating on the Thixotropic Microstructure of AA 7075 Aluminum Alloy via SIMA Process[J]. Journal of Alloys and Compounds, 2011, 509(2): 402-408.

[5] 王雪, 李萍, 朱广余. 3A21铝合金半固态坯料制备工艺研究[J]. 精密成形工程, 2012, 4(6): 71-77.

[6] 陈刚. 高强变形铝合金触变成形及缺陷控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.

[7] 朱广宇, 薛克敏, 李萍, 等. 新SIMA法制备铝合金 3A21 半固态坯料[J]. 精密成形工程, 2010, 2(4): 32-35.

[8] 孟毅. 半固态成形工艺特点及发展现状[J]. 精密成形工程, 2016.(7): 21-28.

[9] 崔成林. 半固态AlSi7Mg合金连铸坯料制备[D]. 北京:北京科技大学, 2002.

Finite Element Analysis of Semi-solid Thixoforming Process of Cylindrical Aluminium Alloy

NIU Hai-xia, ZHANG Qiong

（School of Mechanical Engineering, Anhui Sanlian University, Hefei 230601, China）

Taking the cylindrical A357 aluminum alloy as the research object, through the creation of geometric model, physical model and finite element model, DEFORM finite element simulation analysis software used, the semi-solid thixoforming process of A357 aluminum alloy is analyzed and simulated by finite element method, and the density under different deformation conditions is obtained, and the change rule is found out, which provides technology for the research of semi-solid thixoforming of aluminum alloy.

semi-solid thixoforming; aluminum alloy; finite element analysis; DEFORM

TG146.3

A

1674-3261(2020)04-0240-06

10.15916/j.issn1674-3261.2020.04.007

2019-07-08

安徽省教育厅高校自然科学重点项目（KJ2019A0892）；安徽三联学院科研基金重点课题（KJZD2018007）

牛海侠(1979-)，女，山东菏泽人，副教授，硕士。

责任编校：刘亚兵