基于Dijkstra算法的智能快递柜乡镇选址研究
黄杜鹃,张天圆
基于Dijkstra算法的智能快递柜乡镇选址研究
黄杜鹃1,张天圆2
(1.安徽财经大学 工商管理学院,安徽 蚌埠 233030;2.安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
随着“最后一公里”的逐步深入,以丰巢为代表的各大智能快递柜纷纷进驻社区。但相比城市,对乡镇智能快递柜选址合理化的研究却鲜有涉及。为了弥补以上空白,本文以安徽怀远县下属7个乡镇为例,首先确定了选址的影响因素,其次通过AHP-TOPSIS组合评价模型确定候选乡镇,最后利用Dijkstra算法得到最优选址地点。本研究结果可为我国农村智能快递柜的网络布局,拉动农村电商物流提供有益的借鉴。
智能快递柜;乡镇选址;AHP-TOPSIS组合评价模型;Dijkstra算法
在“互联网+”背景下,我国快递行业得到了飞速发展,由此衍生出的快递柜自进入末端市场以来,凭借“安全、便捷”等特点迅速在国内站稳脚跟,成为“最后一公里”的重要解决方案,并引起学者们的广泛关注。但是他们对快递柜的研究大多聚焦在如市场分析、前景调查等描述性研究上[1-2],对选址的合理化问题涉及不多,忽略了客户体验的重要影响。在仅有的一些研究中,大致可以分为以下两大脉络:第一,在研究思路上,大多以总成本最小化讨论快递柜的投放数量及选址。施书彪等[3]将总成本划分为租金成本、配送成本和惩罚成本,设立了快递柜选址模型,并加以实例检验;第二,在研究对象上,主要针对大学校园的快递柜设置。如张晶蓉[4]讨论了郑州市龙子湖大学城的快递柜选址问题。本文认为,随着乡村网上购物的兴起,加之国家对振兴农村战略的推进,如何解决针对乡镇的末端配送问题意义重大。因此,和以往研究不同,本文将以安徽怀远县7个乡镇为例,利用Dijkstra算法,从地区人口密度和经济意义上的综合评价结果角度对智能快递柜在乡镇的合理布局展开研究。在快递柜的选址上,综合考虑了该地址的经济效益及需求覆盖率最大化因素,纳入了日快递总需求量、人均可支配收入和人口密度等评价指标。在求解算法上,将TOPSIS评价模型和AHP分析法结合起来,简化了AHP分析法处理综合指标的过程,并且提高了TOPSIS模型评价乡镇的准确性。旨在优化乡镇配送网络,进一步释放农村市场活力,拉动消费需求,实现城乡一体化。
1 基于AHP-TOPSIS组合评价模型候选地址的确定
本部分将首先确定选址地区的影响因素,其次采用AHP-TOPSIS方法计算各个影响因素的权重占比,最后将权重大小引入与理想解的相对贴合度的计算,从而对各个乡镇进行排序和评估,得到适合放置快递柜的候选乡镇[5]。
1.1 模型介绍
AHP-TOPSIS组合评价模型主要结合了层次分析法和TOPSIS评价法全面解决问题。其中前者计算影响因素的权重,后者进行评估。通过对评价问题分别构造正、负理想解,即各指标的最优、最劣解,可以将得到的各影响因素的权重来计算每个乡镇被选择设置智能快递柜的合理性到理想乡镇设置快递柜的相对贴近度,即靠近正理想解和远离负理想解的程度,从而对乡镇选择设置智能快递柜的合理程度进行排序并予以评价。在求解与正理想解和负理想解之间的欧氏距离中将使用熵权求和的方法,进而增加评估模型的准确性。
1.2 模型的建立
1.2.1 快递柜选址影响因素的选择
参考主流研究的做法,本文选择日快递总需求量、日平均交通总密度以及人均可支配收入作为该区域快递柜选址的影响因素。

人均可支配收入主要是用于反映该地区居民的消费水平和储蓄水平,指在2个月内各个家庭的人均可支配收入的平均值,记为。
1.2.2 权重向量的确定


图1 怀远县附近的乡镇地理位置图
根据上述影响因素,在数据的选择上,统计了2018年8月—12月流入该地区的快递件数量,1天内观测路段的车辆数,观测路段的长度以及这段时间的人均可支配收入[6],如图2、图3所示。

图2 8—12月份乡村的总快递量

图3 8—12月份乡村的观测路段的车辆数
由图可以看出,在总快递量和总车辆数方面,乡镇11月份的数据一般都比10月份的数据要高一些,并且在11月份的某一段时间出现快递量突增的现象。


表1 1~9标度法规则表
根据表1内容,邀请该领域内学者和企业管理者等相关专家进行打分,比较两两影响因素之间的重要性,从而构造出-比较判断矩阵为:

然后对其判断矩阵进行一致性检验,具体步骤为:
①计算一致性指标

②查找对应的平均随机一致性指标,结果如表2所示。

表2 一致性指标RI表
③计算一致性比例
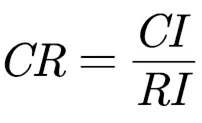
若一致性比例<0.1,则可以接受判断矩阵的一致性,相反若一致性比例大于0.1,则修正判断矩阵。通过公式计算,得到=0.0243,因此判断矩阵具有一致性。
利用算术平均法对上述比较判断矩阵中各因素的权重进行求解,计算步骤具体如下。
①将比较判断矩阵先按照列归一化。
②将归一化的各列相加,即按照行进行求和。
③将相加后的列再归一化即可得出准则层对目标层的权重向量。
通过计算,本文得出-比较判断矩阵的权重向量为(0.4738, 0.2168, 0.3094)T,可见就智能快递柜选址的影响因素而言,其作用程度为日快递总需求量>人均可支配收入>日平均交通总密度(如表3所示)。

表3 乡镇快递柜选址影响因素排序及编号
1.2.3 数据标准化处理
由于上述3个影响因素都是极大型指标,所以不需要对影响因素的数值进行处理。为规避不同量纲对评价结果的影响,使评价体系中的指标可以在相同量纲水平下进行比较,需对原始数据进行标准化处理。具体处理的方法如下:

1.2.4 计算与理想解相对接近度并归一化
1.3 模型的结果与分析
通过AHP-TOPSIS组合评价模型,得到了各个乡镇的相对接近程度W,并对其数值大小进行排序。W指标的数值越大,代表该乡镇设置智能快递柜的合理性越高,反之亦然。因此,本文对各个乡镇的影响因素归一化后,得到如表4所示的排序结果。

表4 AHP-TOPSIS模型结果
根据表4中结果,确定了排序在前4位的乡镇为快递快选址的候选地,即朱岗村、许桥村、普渡村和泰山村。
2 基于Dijkstra算法对候选点到各个地区最短路径的确定
通过对上述候选乡镇的选择,并结合依据乡镇之间相对距离构造的邻接矩阵,下面将利用Dijkstra的标号算法依次计算候选乡镇到其他各个乡镇的最短路径[7-8]。
2.1 Dijkstra算法原理

图4 Dijkstra算法原理图
2.2 模型的求解



④重复第3步,一直到t点得到标号为止。
2.3 模型的结果与分析
为了表示相互地区之间的距离,本文根据7个乡镇的相对位置,以两乡镇之间实际距离的大小代表两乡镇之间的直线距离,并用直线简化地区之间的位置关系(如图5所示)。
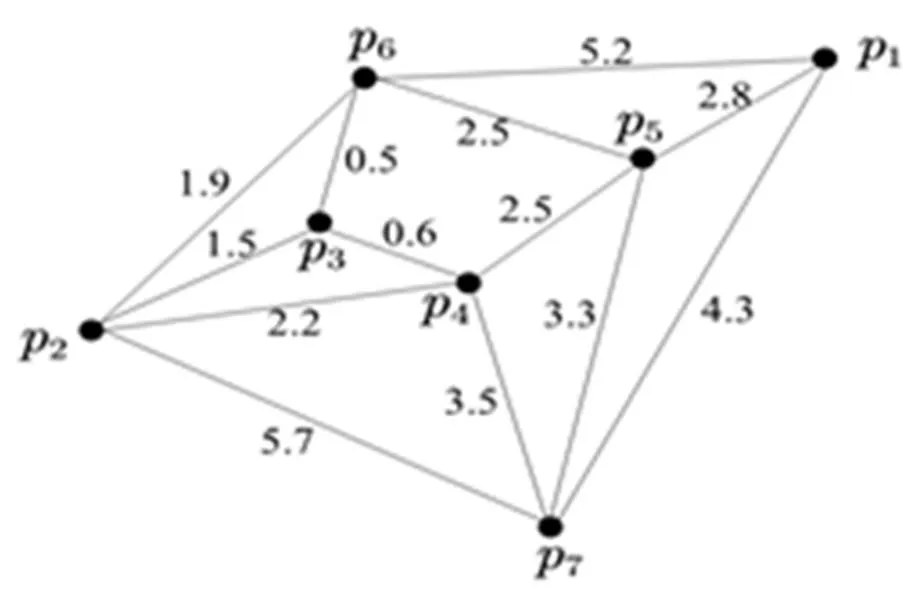
图5 乡镇相对地理位置拓扑图
在乡镇地理位置拓扑图的基础上,通过Dijkstra标号算法来求解建立的模型,得到候选地区到其他各个地区的最短路径的距离,结果如表5所示。

表5 候选地址到其他乡镇最短路径距离表 km
3 智能快递柜最佳选址的确定
以往大多对于最优选址的研究仅以某地到他地的最短距离总和最小为目标,忽略了该地区人口数量对结果的影响。本文采用乡镇人口数与到其他乡镇最短距离的乘积(简称距离人口加权值[9])来判断乡镇放置智能快递柜选址的合理性,并设怀远县附近的候选地区到其他乡镇的最短距离为D,其他乡镇的人数作为计算表达式中最短距离的权重P。根据上述假设,放置智能快递柜的候选地址到其他乡镇的距离人口加权和计算表达式为:

其中S指候选乡镇p的距离人口加权值,=1, 2, 3, 4;=1, 2,…, 7。

表6 候选地址的距离人口加权值表
由表6中结果可知,普渡村的加权值最小,即普渡村是最为合理放置智能快递柜的乡镇。所以在普渡村设置智能快递柜,可以一定程度上提高该乡镇“最后一公里”终端配送的效率。
4 结束语
乡镇智能快递柜的选址问题是现有研究少有涉足的重要问题,与农村配送的高效网络布局息息相关。本文基于AHP-TOPSIS组合评价模型和Dijkstra算法,探索了快递柜选址的合理化。通过对安徽省怀远县下属的7个乡镇为实例对象的研究,结果表明该方法综合了人口密度和经济评价,具有较好的科学性和可行性,对拉动农村电商物流亦大有裨益。
[1] 姜能涛, 吕梦琦. 智能快递柜在城市末端物流应用现状及发展对策研究——以苏州为例[J]. 物流工程与管理, 2019, 41(10): 47-52.
[2] 郑林静. 智能快递柜在高校中推广的前景调查与分析——以江苏师范大学科文学院为例[J]. 中国物流与采购, 2019(23): 42.
[3] 施书彪, 黄有方, 严伟. 智能柜在校园快递配送中的应用研究[J]. 计算机仿真, 2015, 32( 9) : 421-424.
[4] 张晶蓉, 曹沙沙, 王振肖, 等. 大学城内智能快递柜服务网点选址研究—以郑州市龙子湖大学城为例[J]. 物流技术, 2018, 37(4): 23-28.
[5] 王卫红, 王园. 基于PCA-AHP-IE的多指标评价模型研究与应用[J]. 浙江工业大学学报, 2019, 47(6): 591-596.
[6] 徐洋洋, 王山东, 王秀云. 基于Dijkstra改进算法的城市交通阻塞研究[J]. 地理空间信息, 2019, 17(11): 80-82.
[7] 张本俊, 周海娇, 刘淑琴. 改进Dijkstra算法在公共交通出行的研究[J]. 物联网技术, 2018 ,8(11): 45-48.
[8] 李耀庭, 刘怡君, 蔡维晓, 等. 基于改进Dijkstra算法的应急物流路径规划[J]. 军事交通学院学报, 2018, 20(7): 54-58.
[9] 曾志聪, 李嬉慧, 文舒鹏, 等. 基于Dijkstra最短路径算法的校园快递服务集中区选址研究——以五邑大学为例[J]. 现代商业, 2019(5): 174-175.
Research on Location Selection in Villages and Towns of Intelligent Express Cabinet Based on Dijkstra Algorithm
HUANG Du-juan, ZHANG Tian-yuan
(1.School of Business Administration, Anhui University of Finance and Economics, Bengbu 233030, China; 2. School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu 233030, China)
With the gradual deepening of “the last kilometer”, various intelligent express cabinets represented by Fengchao have entered into the community. However, compared with cities, researches on the rationalization of the location of intelligent express cabinets in villages and towns are rarely involved. In order to fill the above gaps, this paper takes 7 subordinate towns in Huaiyuan county, Anhui province as examples, firstly the influencing factors of site selection are determined, then the candidate towns are determined through AHP-TOPSIS combined evaluation model, and finally the optimal site selection is obtained by Dijkstra algorithm. The results of this study can provide useful references for the network layout of intelligent express cabinets in rural areas and the promotion of rural e-commerce logistics.
intelligent express cabinet; villages and towns site selection; AHP-TOPSIS combined evaluation model; Dijkstra algorithm
F251
A
1674-3261(2020)04-0259-05
10.15916/j.issn1674-3261.2020.04.011
2019-12-30
安徽省人文社科研究项目(SK2020A0053);安徽省高校自然科学重点项目(KJ2020A0009);安徽财经大学科研项目(ACKYC19029)
黄杜鹃(1985-),女,安徽蚌埠人,讲师,博士。
责任编校:孙 林

