三点预瞄的智能控制补偿驾驶员模型＊

杨浩 黄超群 魏显坤 税永波

（重庆工商职业学院，重庆 401520）

主题词：三点预瞄 智能控制 驾驶员模型 经验指数模型 补偿校正

1 前言

基于驾驶员的前视作用、推理决策能力和补偿跟踪行为，不同学者分别提出了预瞄驾驶员模型[1-3]、智能控制驾驶员模型[4-6]、补偿校正模型[7-8]。文献[1]基于不同的假设，通过控制横向误差建立了5种单点预瞄模型。文献[2]基于不同的评价指标，通过优化所设置的权重，建立了预瞄时间自适应的驾驶员模型。文献[3]假设驾驶员根据侧向偏差决策出最优加速度变化率，建立了三阶预瞄模型。文献[4]利用神经网络对任意函数的逼近能力，建立了BP 神经网络驾驶员模型。文献[5]通过对一段路程进行预瞄，结合模糊控制，提出了一种路程预瞄驾驶员模型。文献[6]针对转向控制中对于驾驶员参与和驾驶员状态考虑较少的问题，提出一种基于驾驶员状态预测的人机力矩协同转向控制方法，进一步提出驾驶员参与和状态模型预测控制算法。文献[7]提出一种任意车速下校正环节参数的求解方法，用于人-车闭环仿真，具有较高精度。文献[8]提出一种对汽车非线性动力学具有自适应性的复合校正方法，对汽车动力学的非线性特性具有很好的自适应能力。上述方法在路径跟踪方面取得了一定进展，但关于不同预瞄风格驾驶员对预瞄距离的动态调节机制、转向决策的输入与输出量的非线性、补偿校正时期望的稳态转向等问题的分析较少。

为此，本文提出一种三点预瞄的智能控制补偿驾驶员模型，根据前方远、中、近3个点的坐标对目标路径的位置关系进行判断，基于所判定的位置关系和当前车速建立预瞄距离自适应的经验指数模型，逼近不同经验驾驶员对预瞄距离的动态调节过程，根据人-车-路闭环系统的特征建立以车速、航向角、中点侧向误差为变量的三维输入，转向盘转角为输出变量的模糊逻辑智能控制驾驶员模型。最后基于车辆的稳态转向特性，以理想侧向加速度与实际侧向加速的差值进行转向角补偿校正。

2 三点预瞄模型

为逼近真实驾驶员的预瞄跟踪机理，本文设计远、中、近3 个点进行预瞄跟踪，基于所判定的位置关系和当前车速，建立了预瞄距离自适应的经验指数模型，最后选取中点进行横向误差的输出跟踪，如图1所示。

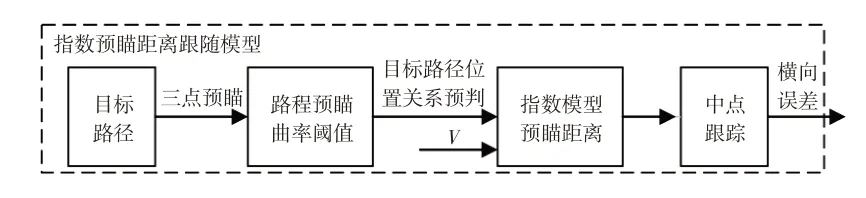
图1 三点预瞄模型结构

2.1 目标路径位置关系判断

驾驶员跟踪的目标路径f（x）往往是直线路径与弯道路径的组合。不妨设f（x）是由直线路径过渡到弯道路径再回到直线路径的一般形式，如图2所示。

图2 三点预瞄模型的几何关系

驾驶员在完成整个路径跟踪时，要依次通过直线路径阶段、直弯过渡阶段、弯道路径阶段、弯直过渡阶段、直线路径阶段5 个组成部分。设驾驶员所处的位置为车辆质心处O，在视线前方x轴方向等间距预瞄了一系列点，计为，其在x轴的坐标值计为2，3，…，n），对应的近点预瞄距离计为di，远点预瞄距离计为di+2，远、近点的距离差值设为di，i+2，相邻两点的距离计为Δd。对应的目标路径上的点计为，相应的侧向误差计为

假设驾驶员在f（x）上预瞄了任意等间距的3个点Ai、Ai+1、Ai+2，对应的坐标值分别为xi、xi+1、xi+2，则f（x）从近点Ai到远点Ai+2的区间上的累积误差为：

式（1）为连续积分，不便应用于工程实际，因此借助Simpson积分算法[9]，用数值计算代替积分计算：

为了判断f（x）在预瞄方向上5个阶段的对应位置关系，做如下几何分析：

Ai+2、Ai与f（x）上对应的Pi+2、Pi所构成梯形的面积（以下简称梯形面积）计为：

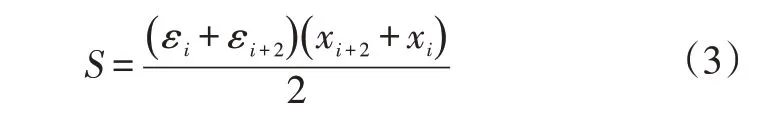
令

基于图2，由εsum与S的几何关系得：q=0时，f（x）为直线路径，如P1P2P3；q＜0 时，f（x）为偏离的弯道路径，如P3P4P5；q＞0 时，f（x）为偏向的弯道路径，如P6P7P8。|q|越大，其道路曲率越大。参考文献[5]，将|q|定义为路程预瞄曲率阈值，通过对q的取值进行判断可得到f（x）相对于预瞄方向的位置关系（直线、偏离或偏向）。

2.2 预瞄距离的经验指数模型

驾驶员预瞄的一般方式为车速越高时预瞄距离越远，目标路径曲率越大时预瞄距离越近。研究表明[10-11]：驾驶员在预瞄跟随时视线集中的范围主要包括“远”（车前方10～20 m）、“近”（车前方6～8 m）2个区域。因此，本文给出预瞄距离自适应的经验指数模型：

式中，d为预瞄距离；η1、η2、η3分别为不同的经验系数，取不同的值代表了不同的预瞄风格；η3体现了驾驶员对预瞄距离的取值下限，本文取η3=6；基于直线路径（q=0）的车速最高为120 km/h，此时预瞄距离应最大，本文取d=18 m，因此，η1=0.1；为简化模型，取η2=1。

2.3 动态三点预瞄策咯

本文采用3个动态点Ai、Ai+1、Ai+2来获取前方f（x）的信息，远、中、近点的预瞄距离满足：

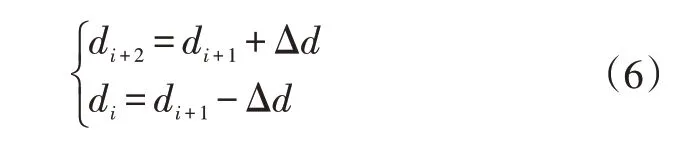
参考远、近点的预瞄区间，其预瞄区域的间隔可取14 m，故式（6）中Δd=7 m。

图3所示为q和d对f（x）的预判机理和远、中、近3个点的动态调节过程。

图3 远、中、近3个点的动态调节示意

当车辆刚进入直线路径（i=1）时，驾驶员在视线前方预瞄了等间距的A1、A2、A3点，对应的f（x）上的点分别为P1、P2、P3。此时εsum=S，即|q|=0恒成立，d处于最大值。

当预瞄视线恰好进入直弯过渡阶段（i=2）时，视线前方预瞄了等间距的A2、A3、A4点，即q=0，d处于最大值。随着预瞄过程的推进，P4点渐进至P5点的过程中，|k|逐渐增大，d由最大值向最小值过渡（如P4P5阶段）。

当预瞄视线完全进入弯道路径阶段（i=4）时，视线前方预瞄了等间距的A4、A5、A6点，即q＜0。同时，|k|保持恒定的最大值，d处于最小值（如P5P6）。

当预瞄视线刚移出弯道路径时，|q|由最大值降至0，d由最小值变至最大值。在之后的弯直过渡和直线阶段，|q|和d的变化规律与直弯过渡阶段相反。

3 转向盘智能控制模型

由于人-车-路闭环系统具有非线性，其精确的数学模型难以建立，而模糊逻辑控制器能够很好地适用于非线性系统，因此，本文将模糊逻辑控制器用于决策转向。

模糊逻辑控制器主要控制流程包含输入变量的模糊化、隶属度函数的选择、模糊规则的制定、模糊推理、解模糊化。本文模糊逻辑控制器的结构为3 维输入、1维输出，以当前车速V、横向误差ε、航向角ψ作为输入变量，输出变量为当前转向盘转角δ0，如图4所示。

图4 转向盘转角模糊逻辑控制器控制流程

3.1 模糊化及隶属度函数选择

我国高速公路最高车速限定为120 km/h，因此将V的基本论域设置为0～120 km/h。参考CarSim 软件中路径宽度为10 m，因此道路中心线与两边界的距离为5 m，将ε的基本论域设置为-5～5 m。根据车辆模型的特性参数和仿真跟踪效果，将ψ的基本论域设置为-30°～30°。参考最大转向盘转角，将δ0的基本论域设置为-540°～540°。V的模糊集论域均为0～5，ε、ψ、δ0的模糊集论域均为-5～5，且输入变量的模糊值y和输出变量的比例因子zk分别为（V的处理方法类似）：

式中，yin、Ymax和Ymin分别为输入变量的精确值、输入变量基本论域的最大值和最小值；zout和zm、Zmax和Zmin分别为输出变量的精确值和模糊值、输出变量基本论域的最大值和最小值。

为了使所设计的控制器具有较高的精确性和灵敏性，定义V的模糊子集为{PS，PM，PB}，ε和ψ的模糊子集为{NM，NS，ZE，PS，PM}，δ0的模糊子集为{NB，NM，NS，ZE，PS，PM，PB}，NB、NM、NS、ZE、PS、PM、PB 分别表示负大、负中、负小、零、正小、正中、正大。输入和输出变量模糊子集的隶属度函数采用三角形函数的形式，如图5所示。

图5 输入与输出变量的隶属度函数

3.2 模糊规则库

模糊规则的制定是模糊逻辑控制器设计的核心部分，它反映了整个控制逻辑的推理过程。本文以V、ε、ψ作为推理的输入量，δ0作为推理的输出量。ε的大小反映了轨迹跟踪的误差，因此，ε越大，期望的δ0越大。ψ反映了车辆的行驶姿态，期望的行驶姿态为车身与道路平行，即ψ应尽快收敛于0。因此，ψ越大，期望的δ0越大。为符合驾驶习惯和提高行驶稳定性，V越大，期望的δ0越小。基于以上分析，建立了模糊控制规则库{R1，…，R75}，定义了75 条判断语句，其中每条语句规则均采用“IFTHEN”判断语句，即

其中，VWi、EWi、ΔWΨ、ΔW分别为Vi、εi、ψi、δ0的模糊语言变量。

模糊控制规则如表1所示。

表1 转向盘控制规则

3.3 模糊推理及解模糊化

为了提高控制算法的速度和精度，采用Mandani模糊推理法。模糊推理后输出的是模糊子集，而车辆模型仅识别精确的控制量，因此需要解模糊化。本文采用重心法解模糊化，该方法主要以隶属度函数和所围成面积的中心坐标作为模糊量的精确值，精确量z为：

式中，zi为输出变量在论域中的值；μzi为zi的隶属度函数值；n为模糊规则的语句总数。

4 转向的稳态补偿校正

高速行驶时轮胎易处于非线性状态，车辆的跟踪稳定性将有所降低，导致跟踪精度下降。此时行驶状态主要表现为侧向加速度较大，而驾驶员所期望的转向状态为稳态转向。因此将理想的稳态侧向加速度与车辆实际侧向加速度的差值作为转向盘转角的补偿校正，补偿转向流程如图6所示。

图6 稳态补偿校正流程

以2自由度车辆模型作为参考模型，其运动微分方程为：

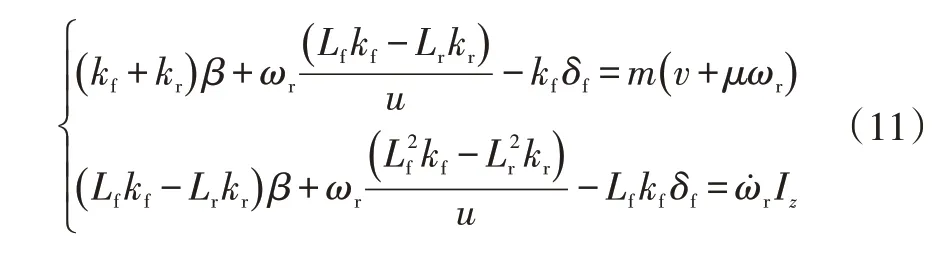
式中，m为整车质量；kf、kr分别为前、后轮胎的等效侧偏刚度；Lf、Lr分别为车辆质心到前、后轴的距离；L=Lf+Lr为轴距；v、u分别为车辆横、纵向速度；β、ωr、δf、Iz分别为质心侧偏角、横摆角速度、前轮转角、转动惯量。

驾驶员在路径跟随时期望的理想状态为稳态转向，即有：

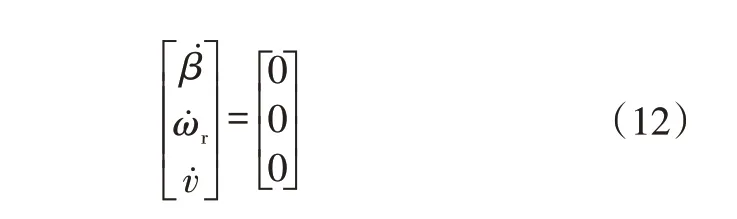
将式（12）带入式（11），得到ωr对δf的增益为：

由转向盘转角与前转向轮的传动关系可知：

式中，δsw、isw分别为转向盘转角和转向系传动比。

将式（14）带入式（13）得到ωr对δsw的增益为：

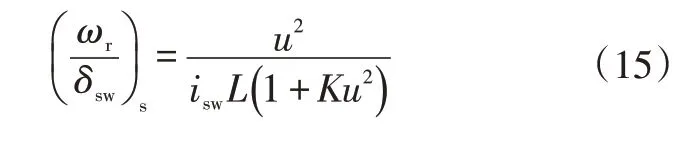
车辆转向时，期望的侧向加速度a2为：

将式（12）和式（15）代入式（16），可得a2对δsw的增益为：

当驾驶员以实际侧向加速度ay进行跟踪时，期望的理想加速度为a2，设Δa=a2-ay，若将车辆的当前时刻冻结，计模糊逻辑控制器输入的当前时刻的转向角为δ0，此时驾驶员对车辆施加额外的转向盘转角Δδsw进行补偿，使得该转角增量补偿Δa为：

式中，kδ为补偿系数，不同的取值代表了不同驾驶员的补偿风格。

但在转向跟踪时，所期望的理想状态是车辆处于稳态特性，结合式（17），kδ可表示为：

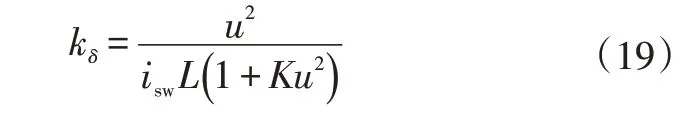
将式（19）带入式（18）可得稳态补偿转角为：

由于稳态时，车辆应处于适当的不足转向，取K=1，稳态补偿转角简化为：

因此，最终决策的转向盘转角为：

式中，δsw为基于δ0和Δδsw之和的有补偿校正模型，δ0为智能控制模型（无补偿校正模型）。

由于预瞄模型仅为δ0和δsw提供f（x）的位置关系，未参与转向角的决策，因此，预瞄模型与δ0和δsw两者之间不存在耦合。

5 仿真验证

为测试本文提出的驾驶员模型路径跟踪的有效性及适应性，跟踪路径分别选择双移线和Alt3路径。双移线路径测试是国际标准的车辆稳定性能测试项目，在一定程度上表现出汽车转向运动的综合能力[12]；Alt3路径是美国高速公路测试路径。根据图6 所示的控制系统模型，结合表2 的仿真参数，基于CarSim 与MATLAB/Simulink 构建的联合仿真平台进行仿真验证，并将有、无补偿校正的2种模型的仿真结果进行对比分析。

表2 仿真参数表

5.1 80 km/h双移线路径跟踪

图7所示为80 km/h双移线路径仿真结果。由图7a可知，有、无补偿校正的2种跟踪方法路径跟踪轨迹与目标路径趋于重合，且跟踪曲线平滑，表明2种方法均具有较好的跟踪效果。在第1个弯道（100 m）处，2条轨迹曲线先于弯道路径进行偏离，表明驾驶员提前预瞄到前方弯道并进行了转向控制。在第2、第3 个弯道（110 m 和160 m）处产生了较小横向误差，在第4 个弯道（170 m）处，跟踪轨迹经过小的超调量后与目标路径趋于重合。由图7b可知，2种方法形成的误差均在-0.8～0.6 m范围内，在4个弯道处产生的横向误差幅值依次在-0.20 m、0.42 m、0.20 m、-0.70 m内，最后经过0.05 m的超调量后误差稳定为0，其中有补偿较无补偿跟踪的侧向误差更小，表明补偿校正可降低横向误差。由图7c 可知，2 种模型的侧向加速度变化趋于一致，均在-0.8g～0.8g范围内，表明有补偿校正模型在提高跟踪精度的情况下并没有增加失稳的风险，兼顾了路径跟踪的有效性和稳定性。由图7d 可知，2 种模型的转向盘转角变化趋于一致，均在-80°～80°范围内，其中有补偿跟踪模型较无补偿跟踪模型所决策的转向盘转角在4 个弯道处有一定增量，用于补偿跟踪误差，提高路径跟踪精度，这也是有补偿跟踪模型的轨迹误差更小的原因。

图7 80 km/h双移线路径仿真结果

5.2 100 km/h双移线路径跟踪

图8 所示为100 km/h 双移线路径仿真结果。由图8a可知，2种跟踪方法路径跟踪轨迹与目标均有一定的横向误差。在第2～4 个弯道处的误差明显增加，2 个模型均经过较大超调量后误差稳定为0。对比图7a可知，随着车速的提高，轨迹误差有所增加。由图8b 可知，2种方法形成的误差均在-1.0～0.8 m 范围内，最后经过0.4 m 的超调量后误差稳定为0。其中有补偿跟踪的侧向误差更小，表明补偿校正可降低误差。对比图7b 可知，随着车速的提高，对应的轨迹误差增加近0.2 m，导致跟踪精度有所降低。由图8c可知，2种模型的侧向加速度在-1g～1g范围内且变化一致，表明补偿校正在降低横向误差时并未增加侧向加速度。对比图7c 可知，侧向加速度增加了0.2g，这也是跟踪误差有所增加的原因。由图8d可知，2种模型的转向盘转角变化趋于一致，均在-80°～80°范围内，其中有补偿跟踪所决策的转向角在4 个弯道处补偿增量均接近10°，用于补偿跟踪误差，这也是有补偿跟踪轨迹误差更小的原因。

图8 100 km/h双移线路径仿真结果

5.3 60 km/h Alt3路径跟踪

图9所示为60 km/h Alt3路径仿真结果。由图9a可知，2 种跟踪方法的跟踪轨迹与目标路径趋于重合，表明在低速时均具有较好的跟踪效果。由图9b 可知，有补偿跟踪模型的侧向误差为-0.2～0.2 m，无补偿跟踪模型的侧向误差为-0.3～0.3 m，表明2 种模型的跟踪精度均较高。在200～400 m、500～600 m、700～900 m的3个弯道处，有补偿较无补偿校正的轨迹误差降低了近0.1 m，表明有补偿跟踪的精度更高。由图9c可知，2种模型的侧向加速度变化趋于一致，均在-0.3g～0.3g范围内，表明有补偿校正模型在提高跟踪精度的情况下并没有增加失稳的风险，兼顾了路径跟踪的有效性和稳定性。由图9d 可知，2 种模型的转向盘转角变化趋于一致，均在-40°～40°范围内，由于轨迹误差小，因此需要补偿校正的量小，导致转向盘转角变化趋于一致。由图9e 可知，当预瞄到0～250 m的直线路径时，d保持了最远距离14.2 m的预瞄跟踪，当进入第1个弯道（250～350 m）时，d由最远14.2 m 自适应地降低到10.5 m，直到驶出弯道进入直线路径350～500 m时，d又从最近10.5 m自适应地升高到14.2 m。在之后的第2、第3个弯道（500～650 m和700～850 m）时，d的动态调节过程与第1 个弯道的调整过程呈周期变化趋势，这与本文建立的三点预瞄动态调节相吻合。

图9 60 km/h Alt3路径仿真结果

5.4 120 km/h Alt3路径跟踪

图10所示为120 km/h Alt3路径仿真结果。

图10 120 km/h Alt3路径仿真结果

由图10a 可知，2 种跟踪方法的跟踪轨迹与目标路径趋于重合，表明在高速时这2种方法也具有较好的跟踪效果。

由图10b可知，有、无补偿跟踪模型的侧向误差分别为-0.6～0.6 m、-0.6～0.8 m，表明2 种模型的跟踪精度均较高，其中补偿校正的跟踪精度更高。在200～400 m、500～600 m、700～900 m的3个弯道处，前2个弯道2种模型的轨迹误差趋于一致，而在第3 个弯道处，有补偿跟踪模型的跟踪误差较无补偿跟踪模型降低了0.25 m，表明补偿校正方法可显著降低轨迹误差。

由图10c可知，在第3个弯道处，2种模型的侧向加速度达到最大值1g，此时车辆处于较大的失稳状态，而补偿校正模型正是基于稳态转向的理想状态，在不增加侧向加速度的情况下，决策出所需补偿的转向角来提高跟踪精度。因此，补偿校正模型在车辆处于较大失稳状态时，对减小轨迹误差的作用更显著。

由图10d 可知，2 种模型的转向盘转角均在-80°～80°范围内，前2个弯道变化趋于一致，在第3个弯道处，有补偿校正较无补偿校正模型增加5°，故轨迹误差降低了0.25 m。

由图10e可知，当在0～250 m的直线路径时，d保持了最远距离18 m 的预瞄跟踪，当进入第1个弯道（250～350 m）时，d自适应地降低到10.5 m，直到驶出弯道进入直线路径（350～500 m）时，d自适应地升高到18 m。在之后的第2、第3个弯道（500～650 m和700～850 m）时，d的动态调节过程与第1个弯道的调整过程往复循环，再次验证了三点预瞄动态调的有效性。

6 结束语

本文提出了一种三点预瞄的智能控制补偿驾驶员模型，给出了适应不同驾驶员预瞄风格的预瞄距离自适应调节策略，建立了转向模糊控制器和稳态转向的补偿校正模型，并基于CarSim 与MATLAB/Simulink 构建联合仿真平台进行仿真验证，结果表明：

a.预瞄距离调节策略能够根据车速和路程预瞄曲率阈值自适应地调节预瞄距离，逼近了不同驾驶员对预瞄距离的决策行为；

b.该模型具有较好的适应性，能够适应从低速到高速的多种复杂工况的跟踪；

c.全程路径跟踪的轨迹误差未超出1 m，表明该模型具有较高的跟踪精度；

d.通过有、无补偿校正的仿真结果对比可知，有补偿较无补偿校正模型的轨迹误差更小，且侧向加速度越大，补偿量也越大，对降低轨迹误差的作用越明显，表明所设计的补偿校正方法是有效的；

e.有补偿校正模型在提高路径跟踪精度时，轨迹误差始终比无补偿校正模型（智能控制模型）小，且在弯道处的补偿效果更明显，同时未额外增加侧向加速度，表明这2种模型之间不存在耦合关系，可以兼顾路径跟踪的有效性和稳定性。