汽车多元动态系统仿真模型响应分析方法*
雷正保 邢欢 陈小勇
(1.长沙理工大学,大型结构碰撞实验室,长沙 410114;2.长沙理工大学,公路工程教育部重点实验室,长沙 410114)
主题词:车辆安全技术 动态系统 模型验证 主成分分析
1 前言
模型仿真技术在一定程度上已经取代物理样机试验成为汽车碰撞安全性能的主要研究工具[1-3],但仿真模型同实际物理对象始终存在一定差距,因此,对其进行验证十分必要。动态系统的高度非线性及复杂性使得模型验证较为困难,主要表现在:动态系统的输出响应数据具有高度的时间相关性和时变性,其相位、幅度及频率等曲线特征差异都需要纳入监控范围,这要求模型验证方法能够全面分析输出响应间的曲线特征差异;复杂动态系统通常包含多个输出响应,且响应间存在着很强的相关性[4],这要求模型验证方法能够有效解决输出响应间的相关性问题;模型验证工作涉及的验证方法较多,实施起来较为繁琐。
针对上述问题,本文基于误差评分法和主成分分析法对动态系统仿真模型的验证方法展开研究。
2 误差评分法
全局误差为时域内每个时间步长具有相同权重时,完整的曲线特征误差。时间响应误差评估(Error Assessment of Response Time Histories,EARTH)方法将全局误差划分为3 个独立的误差,即相位误差、幅度误差和频率误差(拓扑误差)。相位误差为两组时间序列间的总体时间差;幅度误差为无时间滞后时,两组时间序列间的幅度差;频率误差为两组时间序列间的形状差异。这三者分别与信号处理中的相位、幅度及频率相对应,简单的时间序列可表示为正弦函数的形式:

式中,φ为相位;Y为幅度;ω为频率;ti为i点的时间。
相位、幅度及频率三者之间存在着很强的耦合关系,如何对其进行有效测量是本文研究的重点。误差评分法主要分为3 个步骤,即相位误差的测量、幅频误差的测量和误差评分,如图1所示。

图1 误差评分法流程
2.1 相位误差的测量
采用文献[5]中的互相关系数方法进行相位误差测量。该方法通过移动1 个时间序列步长的方式最大化互相关系数,此时,移动的时间步长数eε即为相位误差的线性测量。文献[6]对几种常用的相位误差测量方法进行了对比分析,结果表明,互相关系数方法对相位误差更为敏感,因此,本文在研究过程中选用此方法进行相位误差测量:
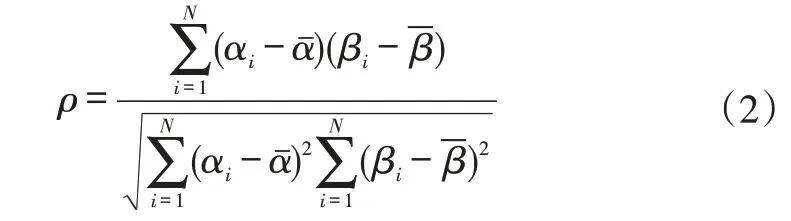
式中,ρ为互相关系数;N为加速度时间序列的长度;αi、βi分别为加速度时间序列i点的实际测量值和理论值;分别为αi、βi的均值。
2.2 幅频误差的测量
幅度误差与频率误差之间存在着很强的耦合关系,独立测量的方式会产生误导性的测量结果,H.Sarin 等曾尝试采用响应误差评估(Error Assessment of Response Time Histories,EARTH)[7]方法对两者进行独立测量,但分离效果不够理想,频率误差的测量结果中包含了过多的幅度信息,这导致最终的验证结果不准确。因此,本文将两者综合考虑,称为幅频误差。
测量幅频误差前,必须最小化由相位误差引起的时间序列间的差异,EARTH 方法通过将原始时间序列移动时间步长数eε的方式对相位误差进行补偿,此方法在某种程度上实现了对相位误差的补偿,但当两条时间序列间的相位误差较大时,需要移动的时间步长数势必较多,此时相移及截短的时间序列无法很好地反映原始时间序列的幅度及频率特性,因此,需要一种新的方法对相位误差进行补偿。
本文拟采用动态时间弯曲距离(Dynamic Time Warping,DTW)算法对原始时间序列进行相位误差补偿,DTW 算法可以通过弯曲时间序列时间轴的方式实现数据点间的错位匹配,这本质上是对数据点的复制与平移,它能够很好地对齐两条时间序列间的波峰和波谷,那么时间序列间的相位误差就可以很好地得到补偿,但此时,DTW 能够反映的主要是幅度信息,如何使得距离矩阵中的基础距离能够同时反映幅度和频率特性是接下来研究的关键。
由式(1)的导数公式可知,去除相位φ的影响后,正弦曲线的导数数据中包含了更多的幅度及频率信息,即对时间序列间的相位误差进行补偿后,其斜率数据间也就包含了更多的幅频误差信息,那么此时两组斜率数据间的动态时间弯曲距离即为幅频误差的测量值。
相位误差eε和幅频误差eφ之间存在数量级差异,从而无法给出直观的评分结果。可以将误差测量值转变为0~100%的数值形式,相位评分Eε和幅频评分Eφ分别为:

相位、幅度及频率三者同为曲线特征的重要度量指标,在进行响应分析时,如何有效确定相关权重一直是研究重点。层次分析法(Analytic Hierarchy Process,AHP)作为一种多目标决策技术,能够定量地分析每个目标的重要程度。文献[8]曾利用AHP 对相位、幅度以及频率在单个评分值间的重要程度进行了定量分析。
文献[9]根据汽车安全模型验证领域的ISO 标准要求以及专家领域知识(Subject Matter Expert,SME)确定各误差评分间的权重,对相位误差、幅度误差以及频率误差的权重分配为1∶1∶1。本文在确定综合评分权重时参考文献[10]的方法,由于本文将幅度误差和频率误差统一为幅频误差来考虑,因此对相位误差和幅频误差的权重分配为1∶2。则最终的误差评分Ee为:
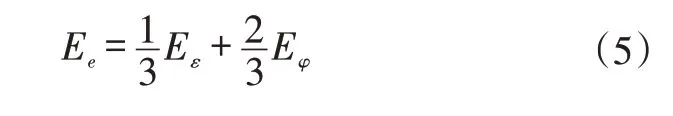
3 主成分分析法的概念及基本思想
3.1 主成分分析的几何意义
传统的降维方法有很多,如主成分分析[11]、核主成分分析[12]和多尺度主成分分析[13]等,其中,主成分分析法是最为常用的一种特征提取方法,能够将高度相关的高维数据映射为相互独立的低维数据[14]。从几何的角度来看,综合变量是向量x1、x2、……、xp构成的坐标系旋转产生的新坐标系。
如图2所示,呈二元正态分布的点大致可形成椭圆形状,沿X1轴、X2轴方向都具有很大的离散性,可以用方差定量表示,如果只考虑1 个方向,将会丢失原始数据中的大量信息,若分别在椭圆的长轴和短轴方向取坐标轴F1和F2,相当于进行了坐标变换,即将原始坐标轴按逆时针方向旋转角度θ,则新坐标与原坐标之间的关系为:
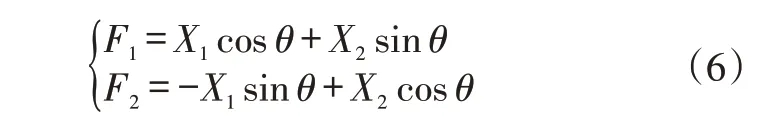
矩阵表示为:
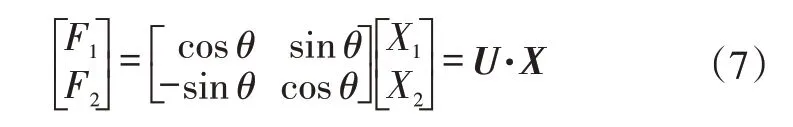
显然UT=U-1,且U为正交矩阵。

图2 主成分的几何意义示意
从图2中可看出,椭圆中的点在F1轴方向上波动较大,在F2轴方向上的波动较小。若椭圆的形状是相对扁平的(短轴非常小),则可以忽略F2轴方向上的波动,此时二维问题便可降为一维问题。一般情况下,p个变量组成p维空间,n个样本是p维空间的n个点,对p元正态分布变量来说,寻找主成分的问题就是寻找p维空间中椭球体的主轴问题。
3.2 主成分分析的步骤
a.首先需要对原始数据进行标准化,主要目的是实现数据的无量纲化及同趋势化。数据无量纲化指的是将不同量纲的原始数据转变为无量纲的新指标数据,使其具有可比性;数据同趋化是指将不同性质的指标数据转换为具有同一性质的新指标数据,使得所有指标的增量方向对测评方案的作用趋势相同。数据标准化的方法主要有“按小数定标标准化”“Z-score 标准化”和“最大值-最小值标准化”等[15]。原始指标数据经过标准化处理后,转换为无量纲且各指标值均处于同一数量级的新指标数据。
b.计算出标准化后数据的协方差矩阵,并计算出该矩阵的特征值及特征向量。
c.确定主成分数量,将求出的特征值按从大到小的顺序排列,若需保留的主成分能反映原始数据95%的信息,则根据≥95%可确定前k个主成分,其中λn为特征向量。
d.根据确定的k个特征值选出与它们相对应的特征向量,将标准化后的原始数据与此特征向量相乘,即可得到前k个主成分。
4 多元响应分析方法
为解决动态系统仿真模型验证中的相关性问题,基于主成分分析法和误差评分法提出了一种多元响应分析方法(Multivariate Responses Analysis,MRA),具体流程如图3所示。

图3 MRA法流程
将降维后的仿真数据和试验数据在同一维度空间中进行比较,最后对试验数据和仿真数据的主成分进行误差评分,由此得到MRA的最终评分公式为:

式中,EM为总误差评分;λj为各主成分权重因子;Ee为各主成分的误差评分。
5 实例验证
选用文献[16]中驾驶员侧乘员约束系统仿真模型对MRA方法进行验证。该模型用于模拟试验车辆100%重叠正面撞击固定刚性壁障,碰撞速度为56 km/h,该试验共有11个响应量[17],响应间相关性较大。设相位阈值为40,幅频阈值为0.2,图4所示为利用主成分分析法提取的试验和仿真数据的前4维主成分。第一、第二、第三和第四主成分分别占原始数据信息的65.4%、20.7%、6.7%和3.2%。
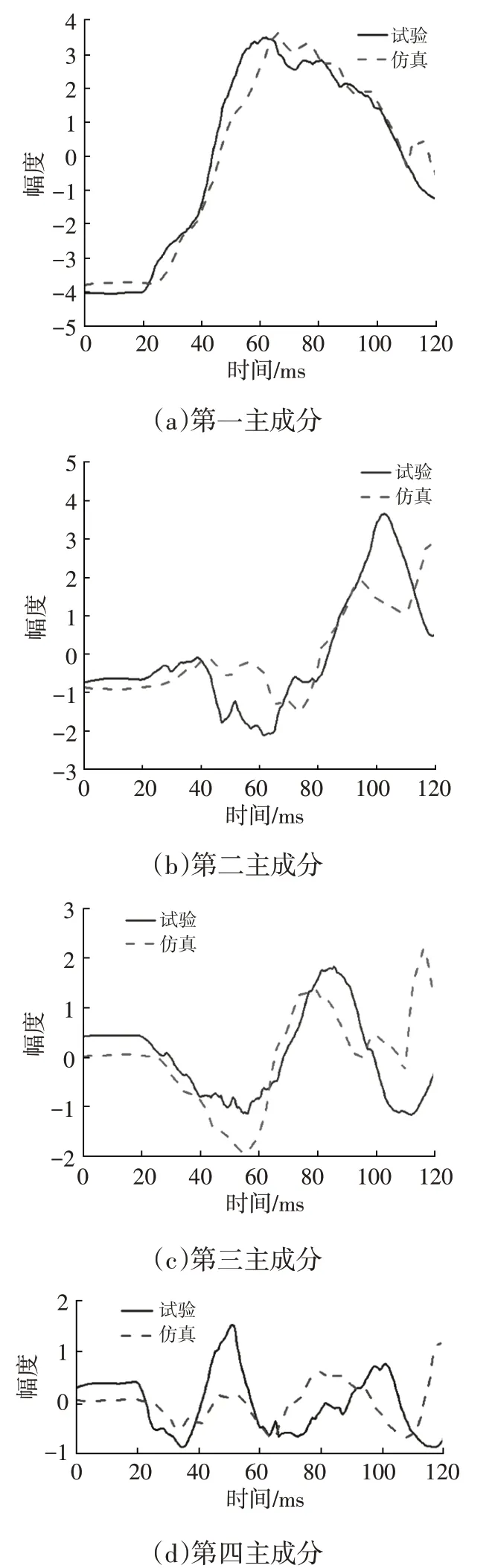
图4 试验和仿真数据前4个主成分对比
使用试验数据各主成分的信息比例加权得到仿真模型的MRA 评分,结果如表1 所示。结合图4 可知,第一主成分的仿真曲线与试验曲线拟合度最高,第四主成分两条曲线的拟合度最低。本文在进行相位误差测量和幅频误差测量时,第一主成分的相位和幅频误差最小,第四主成分的相位和幅频误差最大,这说明本文得到的结果与图4的结果具有一致性,也说明本文提出的方法具有可行性。
原始响应数据误差评分结果的均值为62.25%,两者存在较大差异,这是因为幅度误差和频率误差之间存在强烈的耦合关系,文献[17]对幅度误差和频率误差分别进行测量,这种耦合关系势必对结果造成影响,在进行幅度误差测量时,虽然文献[17]对相位误差和频率误差进行了误差补偿,但是依然存在着局部误差和本地时间误差。本文将幅度误差和频率误差统一为幅频误差,由此解决了动态输出响应相关性问题,这也是本文得到的结果与原始文献的结果具有较大差异的原因,也充分说明解决相关性问题是实现仿真模型有效验证的重要保证。
6 结束语
为了全面分析动态系统输出响应间曲线特征差异,同时解决输出响应间相关性问题,本文基于误差评分法和主成分分析法提出了一种多元响应分析方法,通过降维的方式对11 个响应数据进行了主成分提取,降维后的数据在保留了原始数据足够信息的前提下,大幅简化了计算强度和难度,同时解决了动态输出响应相关性问题,并对各响应进行误差评分。通过误差评分法对输出响应间曲线特征差异进行了全面度量,并通过具体案例验证了该方法的有效性。结果表明,该方法能够直接对多元动态响应间的一致性进行评分,能够全面分析输出响应间的曲线特征差异并消除输出响应间相关性对验证结果的影响。MRA方法受人为影响因素较少,因此,其评分结果更加客观,适用范围也更加广泛。

