基于李雅普诺夫稳定性理论的路径跟踪控制器设计*
郑鑫 赵又群
(南京航空航天大学,南京 210016)
主题词:路径跟踪稳定性LQR自适应控制
1 前言
路径跟踪作为智能车运动控制的核心,已成为国内外学者的研究热点,其最常用的控制手段是模型预测控制(Model Predictive Control,MPC)、最优控制和鲁棒控制。Amir[1]等人针对MPC计算量大的问题,提出了一种利用机器学习选择最佳模型的运行时切换算法,在保证精度的情况下,有效提高了效率。Wang Zejiang[2]等人提出了一种基于查表的在线参数选择方法来提高MPC的效率。Guo Hongyan[3]等人采用微分进化算法对MPC 进行了优化,提高了计算性能和控制性能。Hamid[4]等人为提高控制器鲁棒性,设计了非线性MPC 控制器。Lima[5]等人在MPC 目标函数中综合考虑了平顺性约束。杭鹏[6]等人在分布式驱动汽车上验证了MPC 路径跟踪控制器的可行性。郭应时[7]等人考虑乘坐舒适性,分别对比了基于预瞄和最优控制的控制器跟踪效果。黄海洋[8]等人提出了一种基于多点预瞄最优控制的路径跟踪控制方法,保证了跟踪精度和算法实时性。Zhang Xizheng[9]等人提出了一种最优预见线性二次调节器,实现了精确的路径跟踪和最优的转矩分配。Alipour[10]等人基于轮式移动机器人路径跟踪提出了一种基于滑模鲁棒方法的控制器,提高了系统抗干扰性。Zhao Zhiguo[11]等人提出的紧急转向避撞(Emergency Steering Evasion,ESE)辅助控制器可优化预瞄距离,提高了路径跟踪精度和车辆稳定性。Barbosa[12]等人提出了一种利用鲁棒递推调节器对参数不确定车辆进行路径跟踪和横向控制的方法。
以上路径跟踪研究大多采用MPC,该算法的高计算量使得控制器一般无法满足汽车高速行驶时的实时性,其他算法,如滑模控制中的颤振,对执行机构的可靠性也有很大影响。本文基于李雅普诺夫(Lyapunov)稳定性理论设计模型参考自适应控制器,结合最优控制思想,引入系统反馈补偿矩阵,化为线性二次最优问题,最后利用CarSim/Simulink联合仿真平台,将设计的控制器与MPC在速度和路面附着系数均不同的仿真工况下进行对比。
2 车辆动力学建模
本文的研究目标是使车辆快速而稳定地跟踪目标路径,为了提高控制器的可靠性,降低控制算法的计算量,尽可能地简化动力学模型,本文采用线性二自由度模型作为车辆动力学模型,如图1所示。
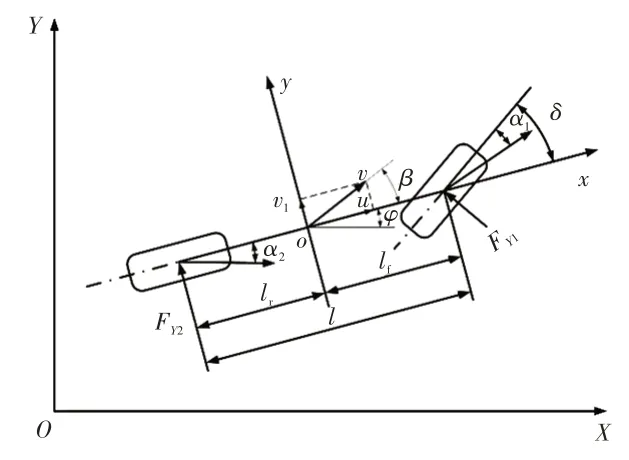
图1 车辆动力学模型
由图1可得汽车二自由度微分方程为:

式中,Ccf、Ccr分别为前、后轮的侧偏刚度;lf、lr分别为质心到前、后轴的距离;φ、β分别为汽车横摆角和质心侧偏角;ω为质心横摆角速度;u为纵向速度;v1为横向速度;δ为前轮转角;m为整车质量;Iz为质心绕z轴的转动惯量。
3 路径跟踪控制器设计
3.1 基于Lyapunov 稳定性理论的模型参考自适应控制器设计
3.1.1 控制系统
本文基于Lyapunov稳定性理论的模型参考自适应控制系统设计了路径跟踪控制器,如图2所示,系统输入为前轮转角δ,uw为汽车模型的输入,系统内环由可调参数前馈控制器、反馈控制器和参考模型组成,系统的外环由自适应机构组成,自适应机构可以自动调整内环可调参数的取值,使被控对象的状态或输出尽可能地跟踪理想值。
根据本文选取的汽车动力学模型,将式(1)写成矩阵形式:

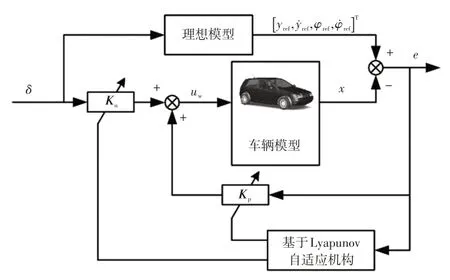
图2 基于Lyapunov稳定性理论的自适应控制器结构
在设计路径跟踪控制器时,参考的输出值分别为理想横向位移yref、理想横向速度、理想横摆角φref和理想横摆角速度,将式(2)代入如下变换:

式中,e1为车辆实际路径与理想路径之间的横向误差;ay为实际横向加速度;ayref为理想横向加速度;e2为实际横摆角φ与理想横摆角φref之间的误差;y为横向位移。
利用误差变量e1和e2可以写出新的误差状态方程:
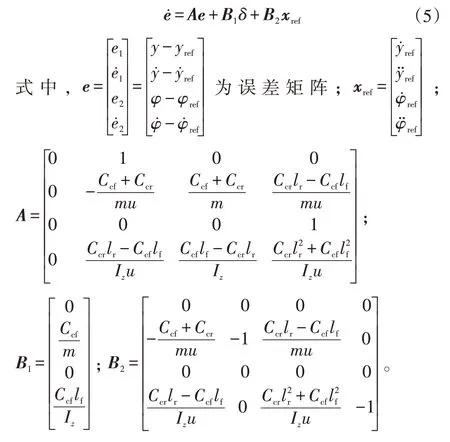
由图2可知,被控对象的输入由反馈控制器和前馈控制器组成:

式中Ku为前馈矩阵;Kp为反馈矩阵。
3.1.2 基于线性二次型最优控制的稳定补偿矩阵求解
本文根据Lyapunov 稳定性理论设计控制器,根据李雅普诺夫第二法,设计能量方程为:

式中,V为能量函数;P为正定矩阵。
设计过程中需要满足:

其中Q也是正定矩阵,由此设计的控制器才能保证系统的稳定性。
而矩阵A的第1 列为0 向量,代入计算发现无法满足上述要求,故本文将反馈控制器Kp写为Kp1和Kp2,其中Kp1作为状态反馈补偿矩阵,保证系统的稳定性,Kp2用作反馈控制器,则将式(6)改写为:

由此,原系统补偿后,新的李雅普诺夫方程有解:
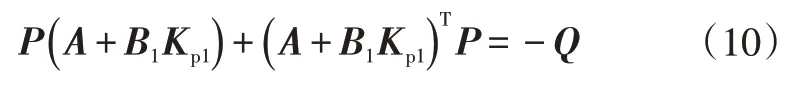
因此,本控制器中P和Kp1的设计也成为关键。则Kp1和P的设计可以由求解线性二次型最优控制(Linear Quadratic Regulator,LQR)问题得出。由于系统中A、B1可控,则Riccati方程必定有解:

由式(11)可设计出P和Kp1。
3.1.3 路径跟踪自适应控制器设计
根据李雅普诺夫第二法,由式(11)求解得到的正定矩阵P构造包含Kp2和Ku的正定二次型能量函数V:

式中,r1、r2为权重系数。
将式(12)对时间求导,得:

将式(9)代入式(13)可得:
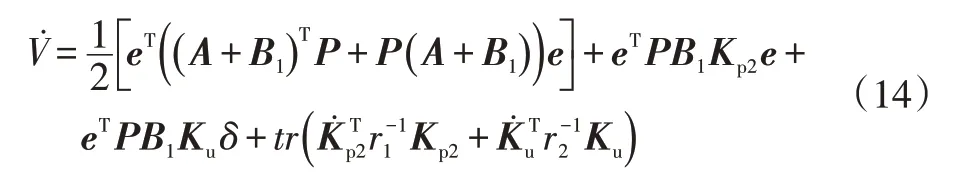
又因为:

则原式(14)转化为:

由李雅普诺夫稳定性理论得到系统稳定的条件为:

由式(10)可知,式(18)一定成立,则Kp2与Ku为:
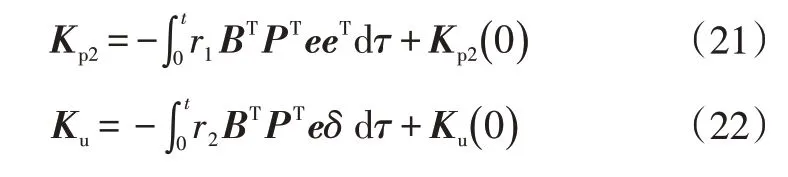
式中,Kp2(0)=0、Ku(0)=0分别为Kp2、Ku的初值。
3.2 模型预测控制器
3.2.1 预测方程
在设计MPC控制器时,需要对汽车纵向运动状态进行预测,在线性二自由度模型基础上考虑纵向运动[13],得到沿x轴、y轴和绕z轴的受力平衡微分方程:
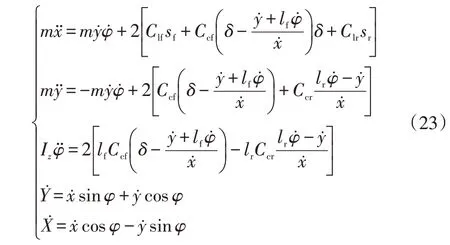
式中,(x,y)为车辆坐标系中的坐标;(X,Y)为地面坐标系中的坐标;Flf=Clfsf、Flr=Clrsr分别为前、后轮纵向力[14];sf、sr分别为前、后轮滑移率。
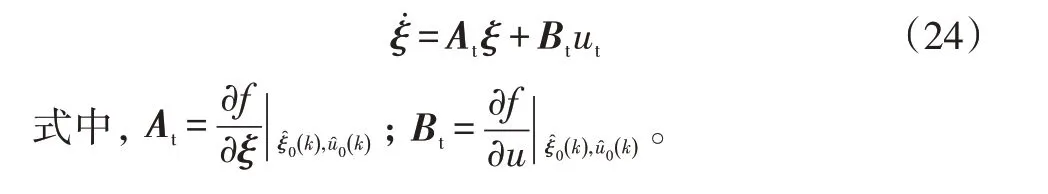
MPC控制器具体见文献[14],本文不再赘述。
3.2.2 约束条件设置
汽车动力学模型是在轮胎侧偏角与侧偏力线性的基础上建立的,对其进行小角度约束:-2.5°<αf<2.5°。
由于汽车的动力性能受轮胎与路面附着条件的限制,假设汽车纵向速度不变[15],考虑乘坐舒适性和小角度模型,横向加速度约束为:-0.4g<ay<0.4g。
质心侧偏角对车辆稳定性也有较大影响,研究表明[16],不同路面下汽车稳定行驶时的质心侧偏角范围为:-12°<β<12°(良好路面);-2°<β<2°(湿滑路面)。
4 CarSim/Simlink联合仿真与结果分析
选取双移线为目标路径,仿真使用的整车参数如表1所示,将本文设计的基于Lyapunov稳定性的模型参考自适应控制器与MPC 控制器控制效果进行对比,仿真过程中分别选取干燥路面(附着系数μ=0.85)、湿滑路面(μ=0.50),起始点为坐标原点,分别以36 km/h、54 km/h、65 km/h的行驶速度进行联合仿真。本文设计的自适应控制器参数如表2所示。
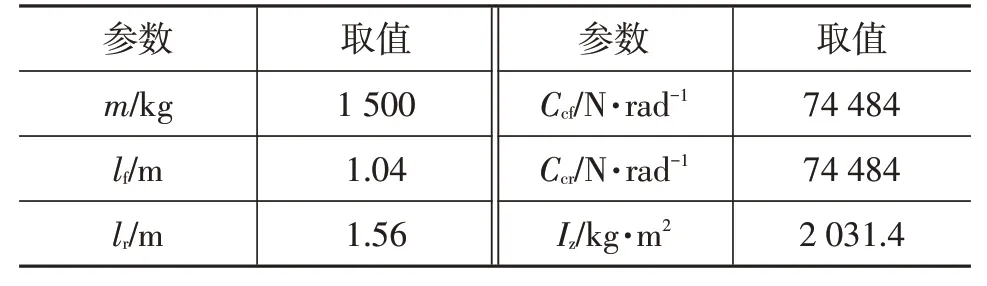
表1 车辆主要参数

表2 自适应控制器参数
为验证本文设计的控制器的可靠性,基于CarSim/Simlink 联合仿真平台对控制器进行对比试验,为验证鲁棒性,仿真过程中保持两控制器的参数不变,仿真结果如图3~图5、表3、表4所示。

图3 干燥路面下不同速度双移线工况仿真结果

图4 湿滑路面下不同速度双移线工况仿真结果

图5 湿滑路面自适应控制器控制下汽车横向加速度

表3 传统MPC控制器实时运行状态
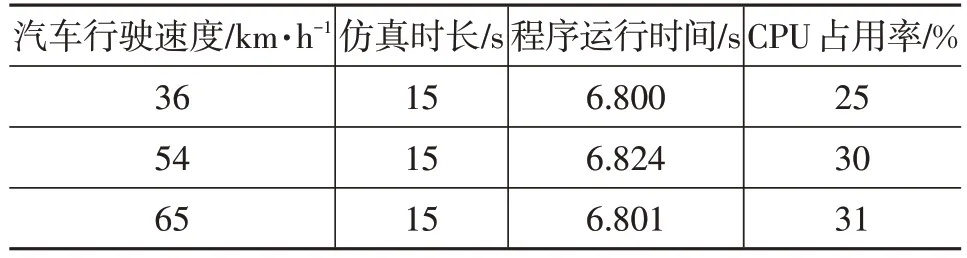
表4 基于Lyapunov的自适应控制器实时运行状态
综合图3、图4可以看出,在保持两控制器参数不变的情况下,基于Lyapunov 自适应控制器的跟踪效果略好于MPC 控制器。由图3b和图3c以及图4a和图4b可以看出,随着车速的提高,基于Lyapunov 自适应控制器的跟踪精度反而略有提高,这是自适应机构中可变系数的前馈控制器和反馈控制器的调节作用造成的。由图4c可知,在湿滑路面上车速为65 km/h时,基于Lyapunov的自适应控制器使汽车行驶过程产生一定误差,但最终回到目标轨迹,这是由于Lyapunov 稳定性第二法在时间趋于无穷时,状态误差趋于0。
由图5可知,虽然在65 km/h的工况下自适应控制器横向加速度出现了抖动,但波动幅度不大,表明汽车处于良好的稳态,抖动的原因可能是轮胎工作于非线性区。
本文联合仿真平台选用酷睿8 代处理器,主频为3.60 GHz,由表3和表4可以看出,MPC控制器程序运行时间较长,超出了设置的仿真时间,并具有较高的CPU占用率,因此,基于Lyapunov 的自适应控制器相对于传统MPC控制器具有较好的实时性。
综上可得,本文设计的基于Lyapunov 稳定性理论的自适应路径跟踪控制器具有良好的路径跟踪效果,保证了系统的稳定性,且在外部环境或自身参数发生变化时有一定的自调节作用,相比于MPC控制器,本算法具有计算量较少、控制精度高且参数调节方便的优点。
5 结束语
本文针对智能车路径跟踪问题,设计了基于Lyapunov 稳定性理论的模型参考自适应路径跟踪控制器,搭建汽车动力学模型,通过CarSim/Simulink 联合仿真平台将该控制器与MPC控制器进行对比,结果表明,本控制算法具有良好的路径跟踪能力和鲁棒性,当外部环境和自身参数变化时,具有一定自调节能力。对汽车非线性模型的研究,高速行驶工况下的系统稳定性和自适应能力以及控制器的鲁棒性是本文后续的研究方向。

