参考系的合理选择与转换
◇ 湖北 饶开宏
良好思维习惯的养成,有助于分析推理能力的不断提高;尊重但不拘泥于习惯和感觉,是提升思维品质的基础.研究物体的复杂机械运动时,合理选择和转换地面之外的参考系,常有拨云见日的神奇功效.
1 以“对方”作为参考系
在研讨“追及与相遇”系列问题时,选定研究对象后,可将被追赶的一方作为参考系.
例1两个身高均为1.6 m 的运动员进行花样蹦床表演,甲运动员挺直竖直跃升的最大高度为15m,在甲跳离蹦床0.2s时,乙挺直竖直跳离蹦床且上升的最大高度为20m,忽略空气阻力影响,g 取10m·s-2,求两人在这一次腾空过程中交错而过的时间.
跳离蹦床时
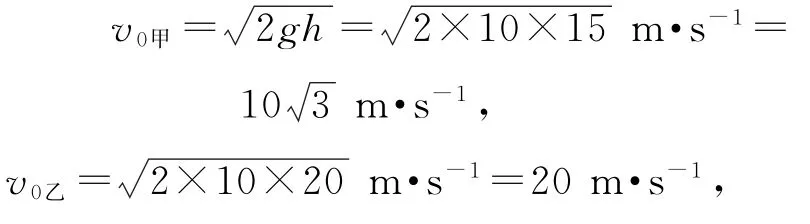
若取乙为研究对象,甲作为参考系,乙相对甲的速度

所以交错时间为

2 “虚拟”参考系
将选定的参考系视作静止,是最基本的处理方法,所以,在研究和比较几个独立物体的运动时,可“虚拟”一个同步进行公共分运动的物体作为参考系,便可将共有的分运动省去,使研究的问题简单化.
例2在空中某一点,同时将A、B 两个小球以大小均为v0的速率分别与水平方向成30°角斜向上和与水平方向成30°角斜向下抛出.忽略空气阻力影响,求抛出后的t 时刻(两球均未碰到其他物体),两球间的距离.
两个小球的运动均可分解为沿初速度方向的匀速运动和竖直方向的落体运动.引入一个同时进行落体运动的物体作为参考系,则A、B 两球均以v0沿初速度方向做匀速直线运动(如图1 所示),xA=xB=v0t,且两个位移的方向成60°角,故t 时刻两球相距xAB=v0t.
当然,若引入一个以v0cos30°水平向右运动的物体为参考系,A、B 的运动分别为v0sin30°的竖直上抛和v0sin30°的竖直下抛运动,可得出同样的结论.
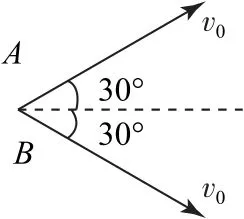
图1
3 以圆心为参考系
有些物理原理或公式在导出的过程中,就已经规定了参考系,我们在运用时只能“照章”处理.如向心加速度的表达式就确定了圆心是最理想的参考系.
例3如图2所示,一光滑细杆水平固定,其上套有一个可自由滑动质量为m 的小环,另用一长为l的、不可伸长的轻质细线一端拴一质量为m 的小球,另一端系于环上.现将小球置于细杆处并使细线恰好伸直,由静止释放小球,重力加速度为g.求:
(1)小球摆到最低点时,细线张力的大小;
(2)细线摆过θ=53°时,细线张力的大小.
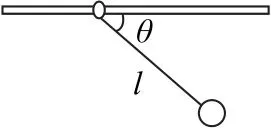
图2
(1)先以地面为参考系将小环和小球当作系统,水平方向动量守恒.设小球到最低点时速率为v1,此时小环速率为v2,设向右为正方向,由动量守恒定律可得mv1-mv2=0,由机械能守恒定律可得联立解得
(2)当细线摆过53°角时,设此时小环速率为v3,小球相对环的速度为v4,以地面为参考系,同理可得

以小环作为参考系,设此时细线张力为F0,由于此时小环对地加速度为a,a =
故以环作为参考系并非惯性参考系,需引入“惯性力”辅助处理,对小球在径向有


图3
4 以质心为参考系
在研究相互间有关联的物体系的运动规律时,可先弄清其“质心”相对地面的运动规律,然后转换以质心作为参考系,进一步分析系统中各物体的相对运动情形,然后将二者综合.
例4如图4所示,质量均为m 的A、B 两相同物块,中间用劲度系数为k 的轻质弹簧相连,静置于光滑的水平面上,现对A 施一沿弹簧轴线水平向右的大小为F 的恒力作用,弹簧始终在弹性限度内,则至少经多长时间A、B 具有相同的向右运动速度?

图4
以水平面为参考系,根据质心运动定理,质心(弹簧的中点)运动的加速度做匀加速直线运动,转换质心为参考系,A、B 均做简谐运动,周期
合理选择参考系对解题十分重要.当涉及动力学和能量及动量问题时,还必须认真审查所选的参考系是否为惯性参考系.
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论

