巧用模型 拓展思维——以轴对称模型的应用为例

范小明

(甘肃省金塔县中学，735300)

在数学解题中，教师要启迪学生思维,教会学生怎样思考，这一点十分重要.我们常常可借助一些实例模型来启迪和拓展学生的思维．举例说明如下.

模型在初中平面几何中，有这样一个问题：如图1,在河边建一泵站向河同岸的甲、乙两个村庄输水.(1)如果要求泵站到甲、乙两村庄的距离相等,泵站M应建在河岸AB上的什么位置?(2)泵站建在河岸AB的什么位置可使铺设的水管最短?

分别用点M，N表示甲、乙两个村庄.

(1)如图2所示，作线段MN的垂直平分线CD交直线AB(河岸)于点Q,Q点处即为泵站修建位置．

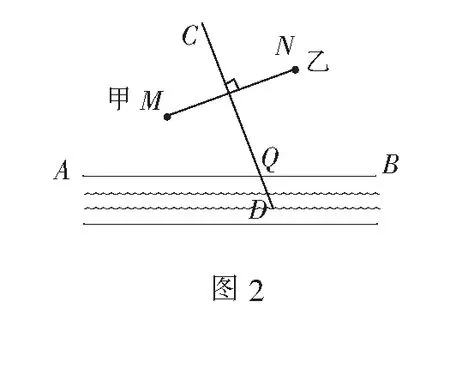
(2)如图3所示，作点M关于直线AB(河岸)的对称点M′,连结MM′交直线AB于点P,P点处即为泵站修建位置．

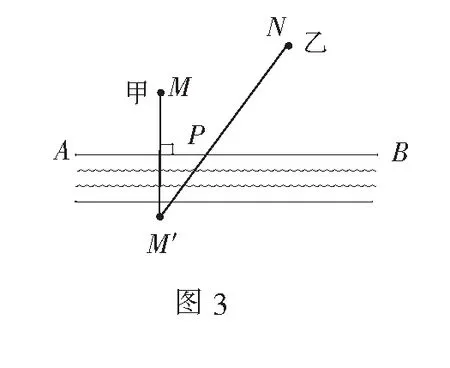
运用上述模型可解决如下问题:

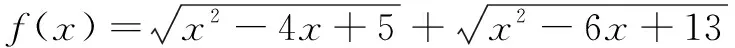
探索与思考拿到这个题目,首先自然想到用函数的单调性或不等式的知识来解决,但直觉告诉我们这样做一定很繁琐.怎么办呢?

将函数式变形为

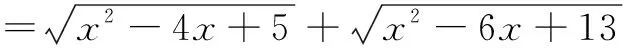
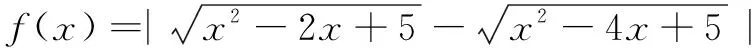
探索与思考本题若按一般求极值的方法很难找到思路,若把根式转化为两点间的距离,利用数形结合的方法,则很容易求得f(x)的最大值与最小值．

将已知条件变形为

故设M(x,0),A(1,2),B(2,1),

∴f(x)=||MA|-|MB||.

则上式的几何意义为x轴上的点M(x,0)到定点A(1,2)与定点B(2,1)的距离的差的绝对值,由上述模型知,所求点为线段AB的垂直平分线与x轴的交点．如图5,当|MA|=|MB|时,f(x)取得最小值0.

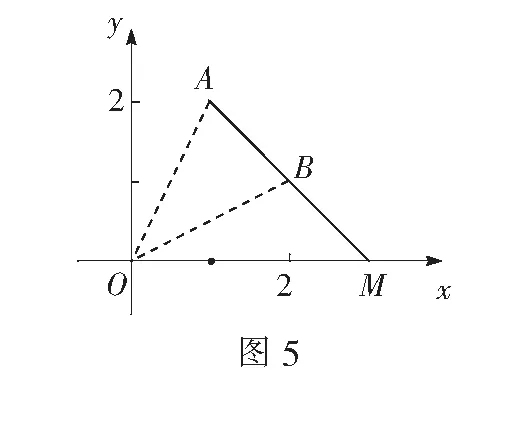
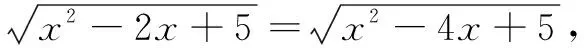
又由三角形的三边关系定理可知,||MA|-|MB||≤|AB|,即当||MA|-|MB||=|AB|,也就是A，B，M三点共线时,f(x)取最大值.

由已知,得直线AB的方程为y=-x+3,令y=0得x=3,

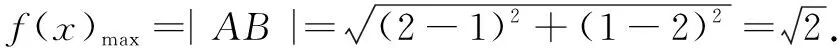
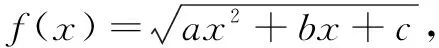
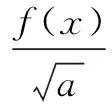
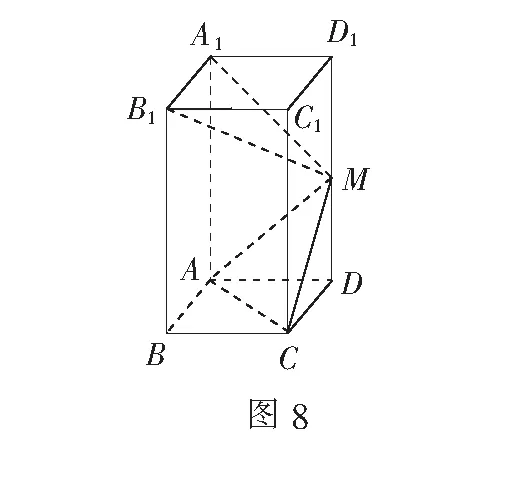
例3(2012年福建高考题)如图6,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.

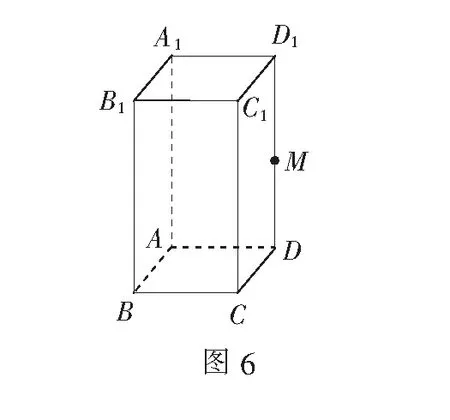
(1)求三棱锥A-MCC1的体积;

(2)当A1M+MC取得最小值时,求证:B1M⊥平面MAC.

解(1)略.

(2)设DM=x则D1M=2-x.

在Rt∆A1D1M中，

在Rt∆CDM中，

由两点间距离公式不难看出,上式表示x轴上的动点P(x,0)到两定点A(2,1)和B(0,1)距离的和．要使A1M+MC的值最小,只需PA+PB的值最小．

如图7,点B′是点B关于x轴的对称点,由平面几何知识不难证明直线AB′与x轴的交点即为所求的点P(1,0),此时x=1,即点M为DD1的中点．

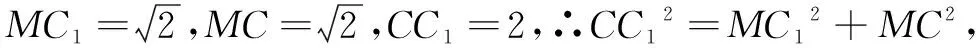
由长方体ABCD-A1B1C1D1知,B1C1⊥平面CDD1C1,∴B1C1⊥CM.

又B1C1∩C1M=C1,∴CM⊥平面B1C1M,得CM⊥B1M.

同理可证,B1M⊥AM.

又AM∩MC=M,∴B1M⊥平面MAC.

例4(2013年重庆高考题)已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( ).

解∵|PM|≥|PC1|-1,

|PN|≥|PC2|-3,

∴|PM|+|PN|≥(|PC1|-1)+(|PC2|-3)=|PC1|+|PC2|-4.

所以当|PC1|+|PC2|取得最小值时,|PM|+|PN|就取得最小值,此问题就转化为在x轴上求一点P,使点P到x轴同侧的两点C1、C2的距离之和最小．利用上述模型便可轻松求解．

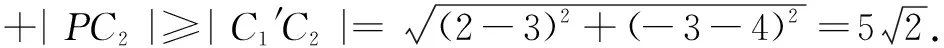
由此可知,在平时的教学或学习中要注意点滴积累,抓住问题的特点，充分利用已有的知识构建数学模型来解决问题,既降低了解题难度，又增加了趣味性．