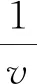
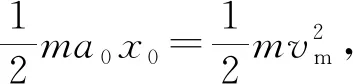探明瞬时斜率 提升核心素养①

蔡蓓蓓 丁杨泉 陆亚军 朱建武

(江苏省南通市如东县马塘中学，江苏 如东 226401)

图线斜率是物理图像的重要内涵之一，探究、揭示图线及其切线斜率的物理意义及变化特征，常成为解决图像问题的关键。当某个物理量y随另一物理量x变化时，若y-x关系图线是曲线，运用“微元思想”实现“化曲为直”，将图线反映的物理变化过程分割成无数小段，则任意一小段图线可看作直线，对应的斜率为k=Δy/Δx。运用“极限思想”，当Δx→0时，Δy/Δx的极限值即为图线上某点切线的斜率，也就是物理变化过程中某一时刻的斜率，故称为瞬时斜率。若能揭示出与瞬时斜率k直接相关物理量的变化情况，便能明快剖析、推断图像的变化特征。在高中物理图像教学中，通过引导学生探明图线上瞬时斜率的内涵，使之理解掌握相关物理观念和思想方法，可有效训练科学思维，提升科学探究能力，养成科学态度，从而切实提升学生的物理学科核心素养。

1 熟悉瞬时斜率的两种特征及应用

以v-t图像为例，运用微元思想易知：v-t图线与横轴所围成的“面积”表示位移，“面积”的正、负表示位移的方向；v-t图线的瞬时斜率表示加速度，瞬时斜率的正、负对应加速度的方向。

(1) 当v-t图像为折线时，其瞬时斜率为阶段性定值，常可用来进行定量分析、推算。

例1：某竖井中矿车两次不同的提升过程，其速度随时间变化关系如图1中图线①、②所示，变速阶段加速度的大小都相同，提升相同的高度，求对应的上升位移所用时间之比。

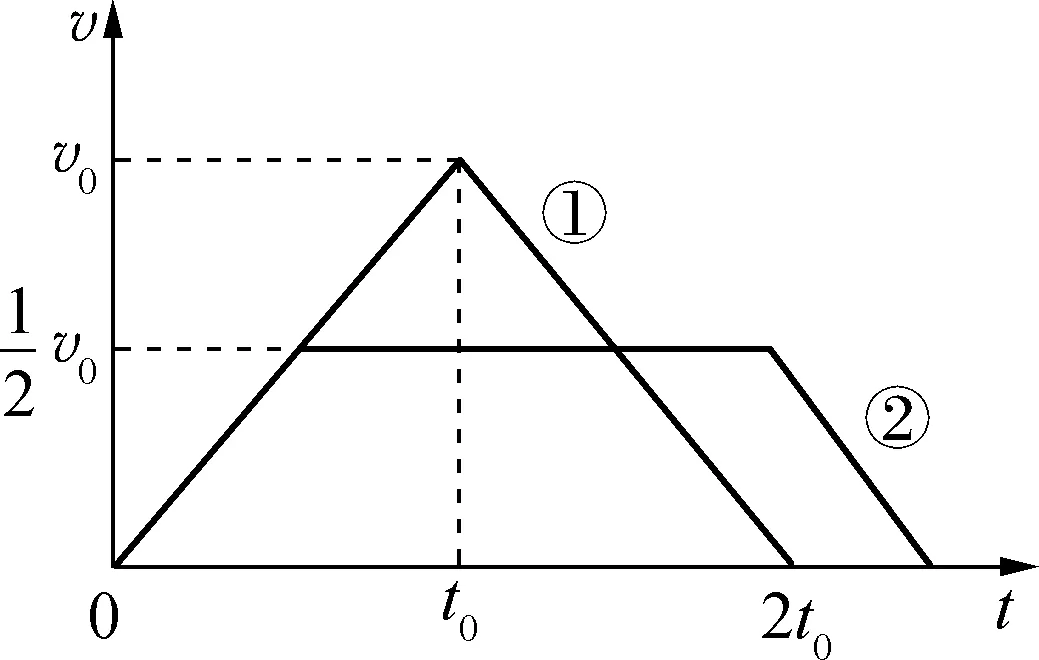
图1

解析：变速阶段加速度大小相同，即图线瞬时斜率绝对值相同，则①、②图线分别为等腰三角形、等腰梯形。上升位移相同，则①、②图线与横轴围成的“面积”相等，图像中顶部三角形与右侧平行四边形的“面积”也相等，所求之比为4∶5。

(2) 当v-t图像为曲线形时，其瞬时斜率不断改变，可用来进行定性或半定量分析。

例2：甲、乙两汽车在同一条平直公路上同向运动，其速度与时间关系的图像分别如图2中甲、乙两条曲线所示。已知两车在t2时刻并排行驶，则两车在t1时刻也并排行驶吗？两车的加速度是如何变化的？

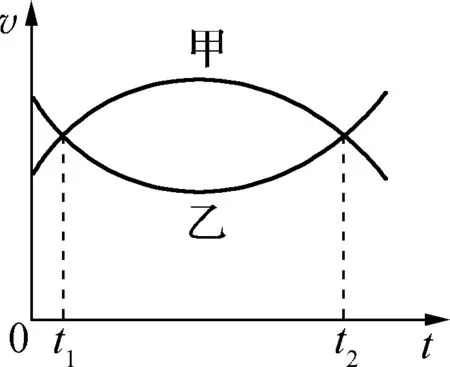
图2

解析：显然在t1～t2时间内甲车位移较大，则在t1时刻乙车在前、甲车在后。两车的瞬时加速度大小即为瞬时斜率的绝对值，都是先减小后增大，但加速度方向即瞬时斜率的正、负表明：甲车加速度方向先正、后负，而乙车恰恰相反。

2 掌握判断图像特征的两种方法

以动能与时间关系的Ek-t图像为例，分析、推断图像特征常有两种方法：(1) 函数式法。推出动能Ek与时间t的函数关系式，据此进行判断。(2) 瞬时斜率法。探究、揭示图线瞬时斜率的物理意义及变化特征，据此进行判断。

例3：从地面竖直向上抛出的小球，运动一段时间后落回地面。忽略空气阻力，该过程中小球动能Ek与时间t的关系图像有什么特征？

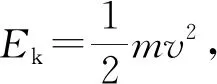
3 体验运用瞬时斜率法的简便性

先以速度与位移关系的v-x图像为例，匀变速直线运动中速度与位移非一次函数关系，综合运用运动学规律公式和数学中圆锥曲线知识，推理、判断其v-x图像的特征较为麻烦。如探究、揭示出图线瞬时斜率的物理意义，其分析过程较简明。

例4：一汽车从静止开始做匀加速直线运动，然后刹车做匀减速直线运动，直到停止。该过程中速度v和位移x的关系图像有什么特征？

解析：通过函数式法分析的确较麻烦，可挖掘v-x图像中图线切线斜率的物理意义：而Δv=aΔt，Δx/Δt的极限值为瞬时速度v，加速度a为定值，所以切线斜率k=a/v，表明瞬时斜率与瞬时速度成反比，即瞬时斜率绝对值随瞬时速度大小变化，在加速阶段|k|逐渐减小，在减速阶段|k|逐渐增大，两个阶段的图线都向下弯曲。

再以Ek-x图像为例，即使能推出动能Ek与位移x的函数关系式，也不如揭示图线瞬时斜率的物理意义来得简便。

例5：一小物块沿斜面向上滑动，然后滑回原处。物块初动能为Ek0，与斜面间的动摩擦因数不变，则该过程中物块动能Ek与位移x关系的图线有什么特征？

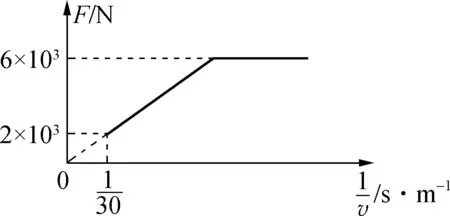
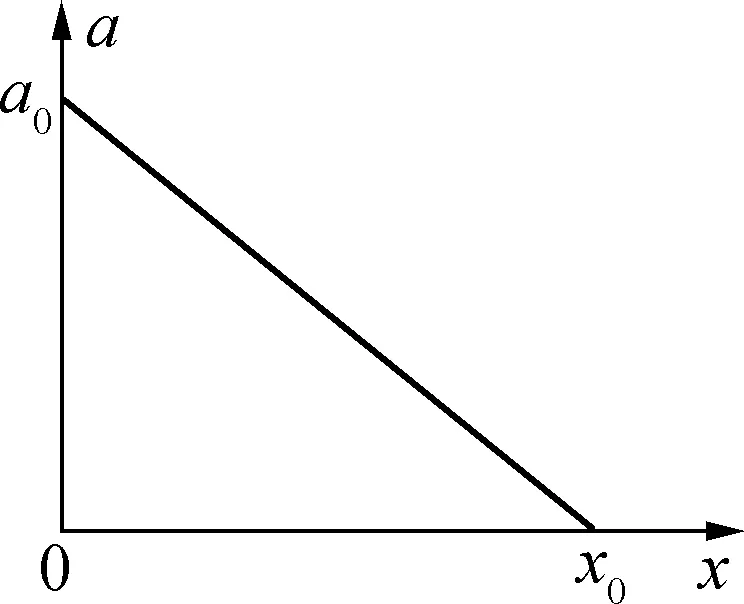
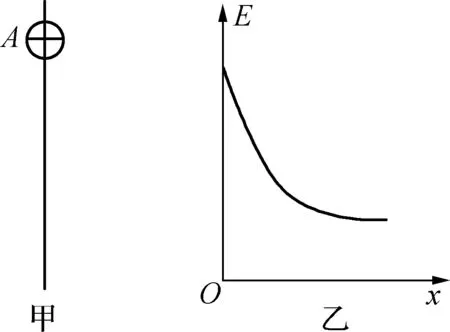
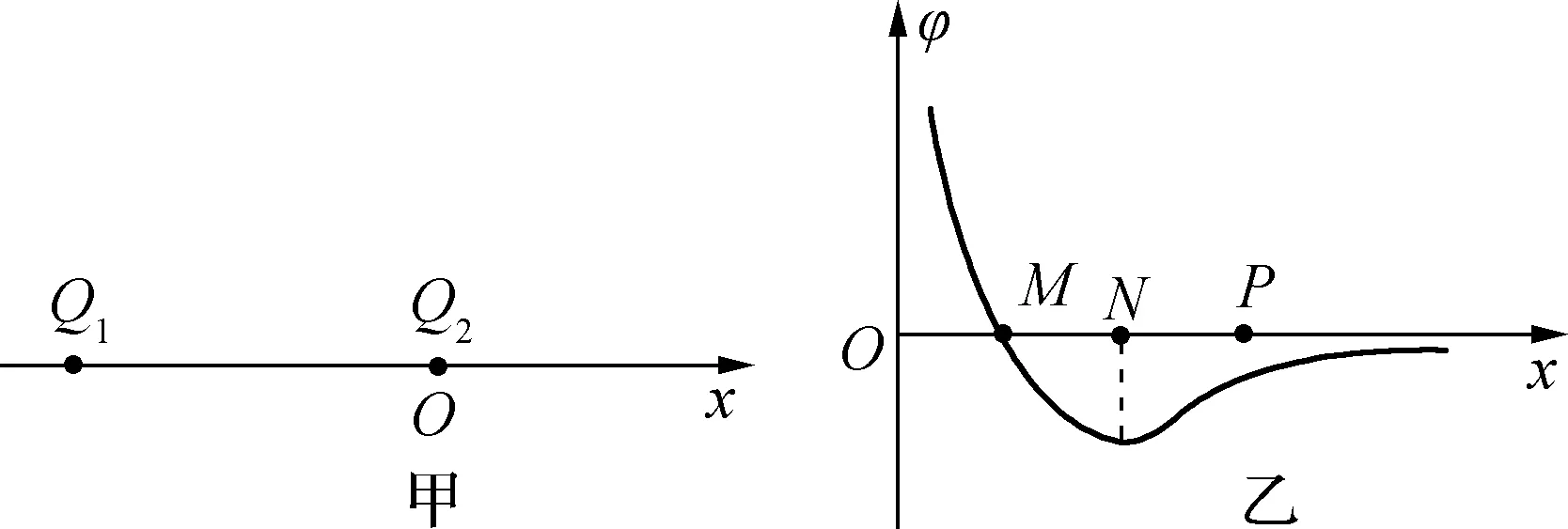
解析：小物块可视为质点，先沿斜面向上滑动到最高点，然后向下滑回到原处；相应的位移x先变大，在最高点时x坐标值最大，此后x坐标值变小，回到原处时x=0；物块的动能Ek先变小，在最高点时Ek=0，此后Ek变大，回到原处时动能Ek

4 运用瞬时斜率法，举一反三

先以机械能与位移关系的E-x图像为例，根据功能关系，除重力以外的力所做功等于物体机械能的变化，即ΔE=W外=F外Δx，所以在机械能与位移关系的E-x图像中，图线的切线斜率k=F外，因此除重力以外的力F外的方向和大小直接决定了瞬时斜率k的正负及其大小。

例6：某空间区域中有竖直方向的电场(图3甲中只画出了一条电场线)，一个质量为m、电荷量为q的带正电小球在电场中从A点由静止开始沿电场线竖直向下运动，不计空气阻力，此过程中小球的机械能E与小球位移x关系的图像如图3乙所示，由此可以判断( )。

图3

A. 小球所处的电场为非匀强电场，且场强不断减小，场强方向向上

B. 小球所处的电场为匀强电场，场强方向向下

C. 小球可能先做加速运动，后做匀速运动

D. 小球一定做加速运动，且加速度不断减小

解析：因为瞬时斜率k=F外=F电=qE′，所以瞬时斜率k与场强E′成正比。随着小球下落位移x增大，小球的机械能E在减小，表明电场力做负功，场强E′方向向上；且斜率k绝对值在减小，则场强不断减小，小球所处的电场为非匀强电场；小球所受向上的电场力一直减小，则它一直做加速运动，且瞬时加速度不断增大，选项A正确。可推论：当斜率k=0时场强E′=0，机械能E不随下落位移x变化。

再以电势与位移关系的φ-x图像为例，图线上切线斜率即瞬时斜率k=-E，E为对应位置的场强。

例7： 如图4甲所示，x轴上固定两个点电荷Q1、Q2(Q2位于坐标原点O)，其上有M、N、P三点，间距MN=NP，Q1、Q2在轴上产生的电势φ随x变化关系如图4乙，则( )。

图4

A.M点电场场强大小为零

B.Q1、Q2为异种电荷,且Q2电荷量值较小

C.M、N之间电场方向沿x轴负方向

D. 一正试探电荷从P移到M的过程中，电场力做功|WPN|=|WNM|

解析：由于M、N、P三点位于点电荷Q1、Q2连线的Q2外侧延长线上，在N点时的瞬时斜率k=E=0，选项B正确；在M点的瞬时斜率k=E≠0，选项A错误；M、N之间瞬时斜率k=E<0，电场方向沿x轴正方向，选项C错误；一正试探电荷从P移到M的过程中，电场力做功W=qU，而|UPN|<|UNM|，选项D错误。

5 密切联系实际，谨防思维定势

运用瞬时斜率法时，也得紧密联系物理过程的实际。

图5

A. 阻力为2×103N

B. 车速为15m/s时功率为6×104W

C. 匀加速运动加速度为3m/s2

D. 匀加速所需时间为5s

再以a-x图像为例，说明“瞬时斜率法”并非总能应用。

例9： 一物体由静止开始运动，其加速度a与位移x关系图线如图6所示，则该物体( )。

图6

A. 最终静止

结合以上例题的应用，学生既能明了图线瞬时斜率的内涵，化难为易处理图像问题，又能学会思想方法、举一反三，还能注重联系实际，防止想当然。