均匀异号电荷等大共轴圆板轴线上电场均匀性研究*

周群益

（广州理工学院通识教育学院 广东 广州 510540）

钟 铮

（赣州市第一中学 江西 赣州 341000）

莫云飞

（长沙学院电子信息与电气工程学院 湖南 长沙 410022）

侯兆阳

（长安大学理学院 陕西 西安 710064）

1 引言

对于均匀带电圆形薄板，为了计算轴线上的电场强度，许多教材根据电势叠加原理首先推导出电势公式［1～4］

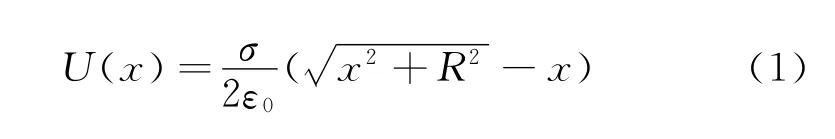
其中，σ是电荷的面密度，ε0是真空介电常数，R是圆板的半径，x是过中心垂直于盘面的轴线上场点的坐标.再利用场强与电势的关系推导电场强度

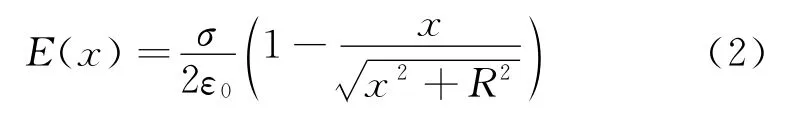
也有教材和习题解答直接利用场强叠加原理推导上式［1～5］.不过，这些公式只适合于x＞0的情况.本文利用电势叠加原理计算轴线上的电势，再利用场强与电势的关系重新建立了轴线上的场强公式，用图形说明了电势和场强的分布规律.

人们通常将一对半径相等共轴带均匀异号电荷的薄圆板当作平行板电容器，这并不正确，因为均匀带电圆板并不是导体.本文专门研究了均匀带正负电荷的共轴圆板在轴线上的电场强度，发现轴线上的电场并不均匀，中间是极小值，用图形直观地显示电场的分布规律.文本提出了均匀系数的概念，衡量电场的均匀程度.用图形说明了均匀系数与两板之间距离的关系.

2 均匀带电薄圆板在轴线上产生的电势和场强

均匀带电薄圆板如图1所示，其半径为R，电荷的面密度为σ（σ＞0）.

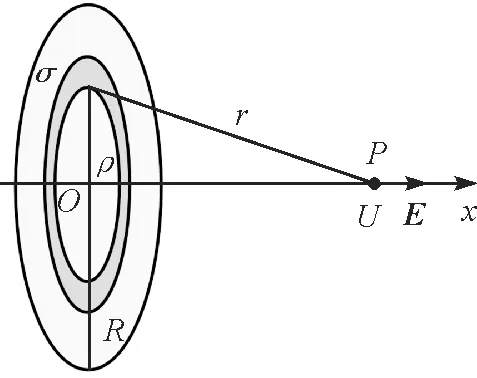
图1 均匀带电薄圆板在轴线上产生的电势和场强

在半径为ρ处取宽为dρ的一个圆环，其面积为

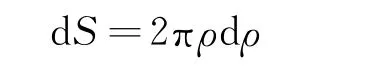
所带电荷量为

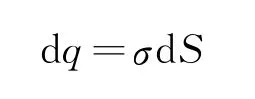
环电荷到轴线上的场点P的距离为

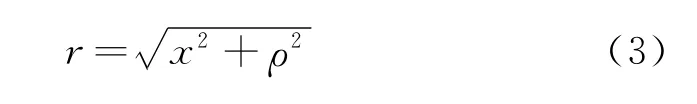
dq在P点产生的电势为

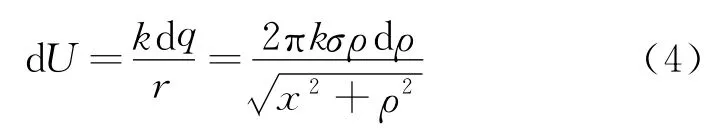
其中，k是静电力恒量.取无穷远处为电势零点，利用凑积分法，点P的电势为

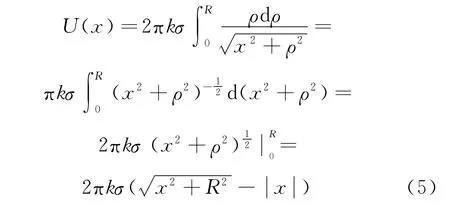
式（5）与式（1）相比，式（5）中出现了绝对值函数.

符号函数定义为

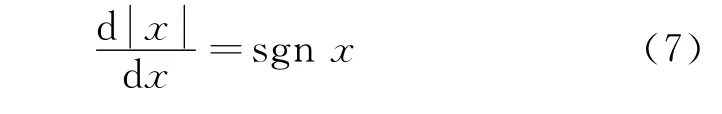
利用绝对值函数的导数的公式，场强为

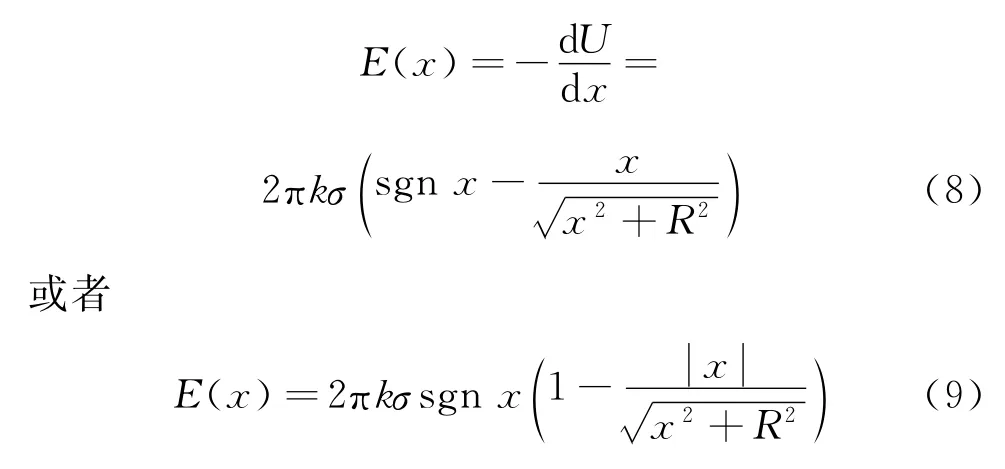
式（9）与式（2）相比，式（9）中多了绝对值函数和符号函数.笔者曾在文献［6］中利用绝对值函数表示电势和场强.在此，对薄圆板轴线上的场强和电势讨论如下：

（1）当R→+∞时，圆板变成无限大平板，在板两边产生的场强为

可见：均匀带电圆形薄板在远处的电势和场强接近于点电荷的电势和场强.

（3）当x=0时，场强为E（0）=0，这是因为圆板内部的场强为零.当x→0+时，sgnx→1，可得圆板正面的场强

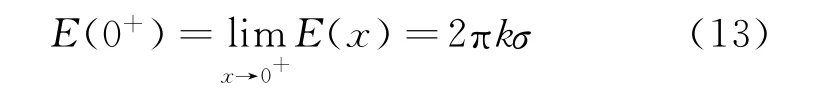
当x→0-时，sgnx→-1，可得反面的场强

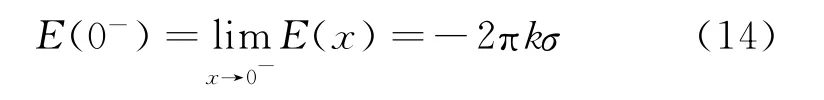
可见：圆板表面的场强等于无限大均匀带电平面在空间产生的场强（忽略圆板厚度）.

3 场强的无量纲化和可视化

取R为坐标单位，取U0=2πkσR=为电势单位，则轴线上无量纲的电势为

点电荷的无量纲电势为

点电荷的无量纲场强为

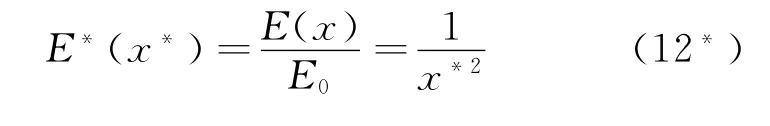
利用M ATLAB的函数很容易计算电势和电场强度，利用作图指令plot可画出函数曲线.

如图2（a）所示，均匀带电圆形薄板在轴线上的电势U（x）是偶对称曲线，在x=0处是一个尖点；当很大时，其电势接近于点电荷的电势.如图2（b）所示，均匀带电圆形薄板在轴线上的场强E（x）是奇对称曲线，在x=0处是一个间断点：E（0+）=E0，E（0-）=-E0，这是薄板两个表面的场强.由于U（x）在x=0处是一个尖点，其导数并不存在，E（0）=0是补充值，表示薄板内部的场强.当很大时，圆形薄板的场强接近于点电荷的场强.

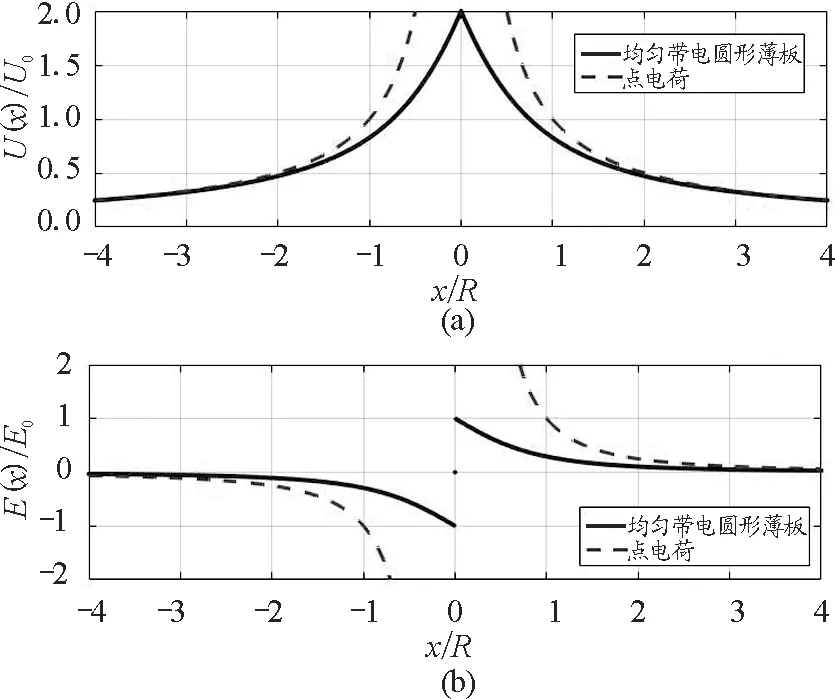
图2 均匀带电圆板在轴线上的电势和场强

4 均匀等量异号带电圆板共轴线上的电势和场强

如图3所示，两个圆形薄板共轴，分别带有面电荷密度为σ的正负电荷，组成一对均匀带等量异号电荷的薄圆板.设两板相距为2d（d称为半距），取x轴为横轴，则轴线上点P的电势是两个圆形薄板电荷产生的电势之和

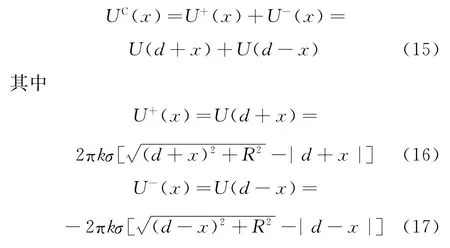
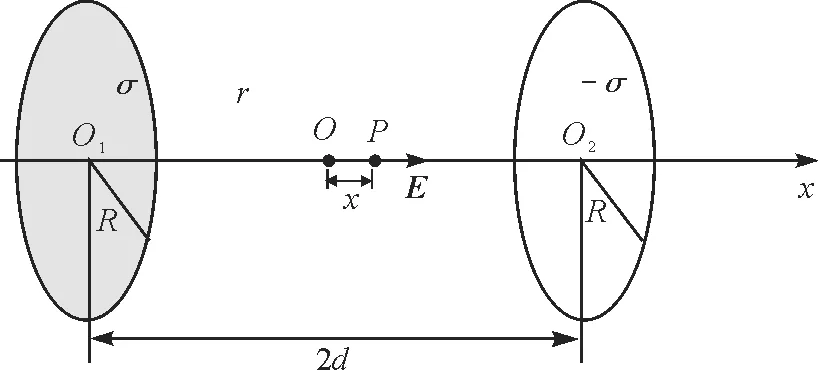
图3 均匀等量异号带电圆板共轴线上的场强

点P的电场强度是两个圆形薄板电荷产生场强的叠加，由于轴线上的场强均沿x轴方向，则总场强

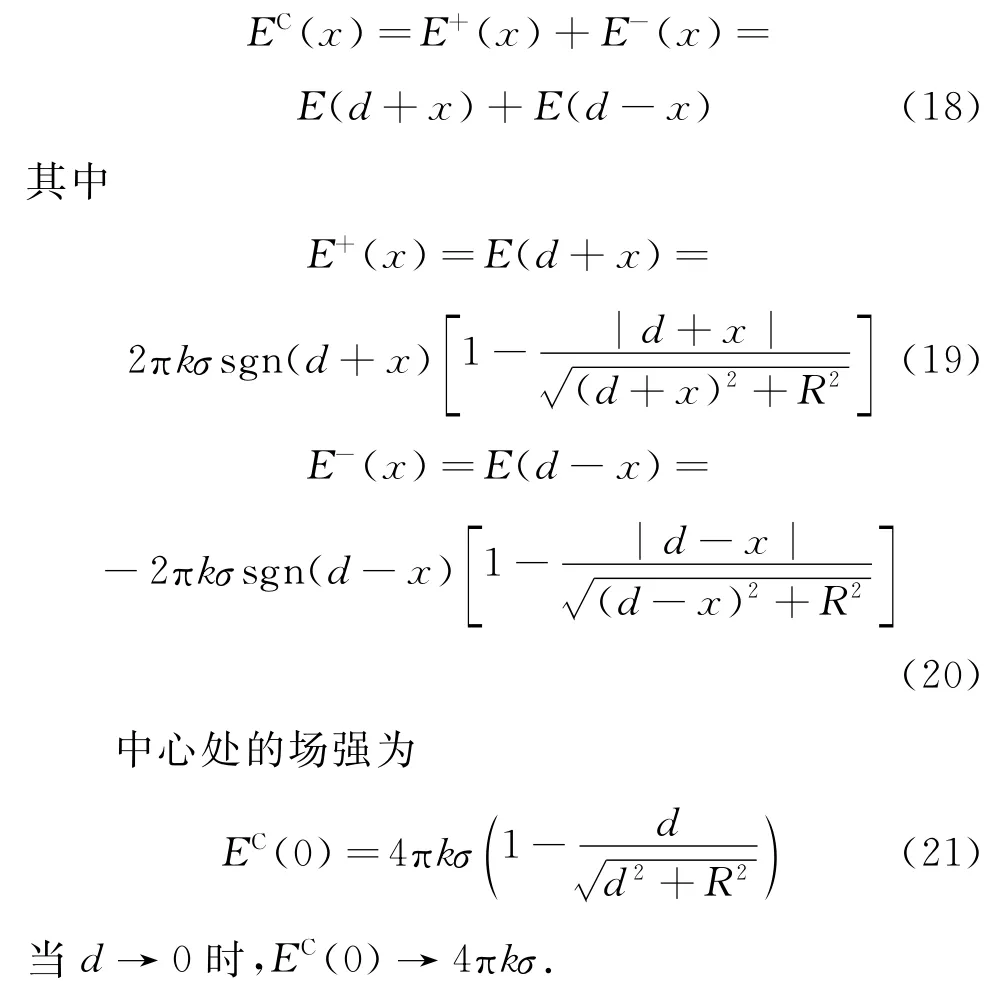
一个均匀带电圆形薄板的场强E（x）对x的导数为

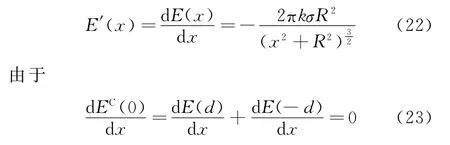
所以EC（0）在x=0处是驻点.E（x）对x的二阶导数为

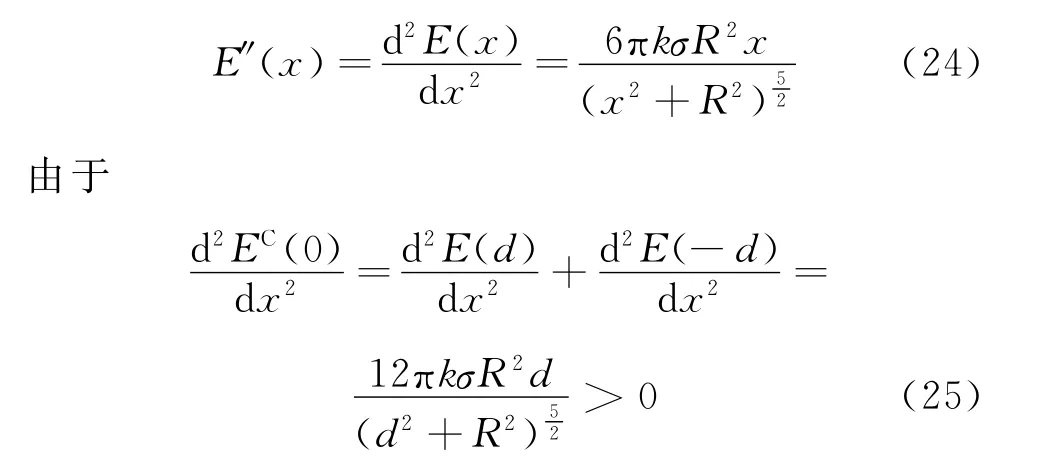
所以EC（x）在x=0处是极小值，说明中心附近的场强并不是均匀的.

在右板的左表面，x=d-，场强为

在左板的右表面，x=-d+，场强为EC（-d+）=EC（d-），即：圆形薄板内表面的场强相等.当d→0时，EC（d-）→4πkσ.

EC（d-）或EC（-d+）与EC（0）之差反映轴线上电场的均匀特性，因此可定义无量纲的均匀系数

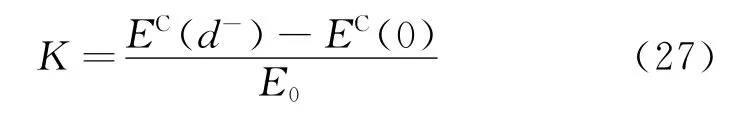
将式（21）和式（26）代入上式，可得

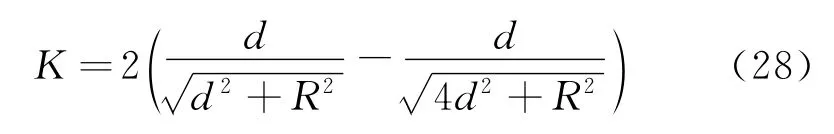
均匀系数K取决于半距d.K越大，表示场强越不均匀.

5 均匀等量异号带电圆板共轴线上场强的可视化

取R为坐标单位，取U0为电势单位，取E0为场强单位，可以把电势和场强公式无量纲化，也可以将中心和内边缘的电场无量纲化.通过图形可以显示场强叠加的结果和均匀系数随距离的变化规律.

如图4（a）所示，取圆形薄板的半距d=0.2R（大小可以根据需要选取），尽管U+（x）和U-（x）是非奇非偶函数，但是其和UC（x）是奇函数曲线，尖点在x=±d处，两板之间UC（x）曲线经过原点，几乎直线下降.如图4（b）所示，尽管E+（x）和E-（x）是非奇非偶函数，但是其和EC（x）是偶函数曲线，跳跃点在x=±d处；两板之间的场强EC（x）比较平，在x=0处处微微下凹，是极小值；两板之外的场强比较小，方向与板内场强的方向相反.当半距d不同时，合电势UC（x）与合场强EC（x）曲线会发生一些改变，但是大体形状不变（图略）.

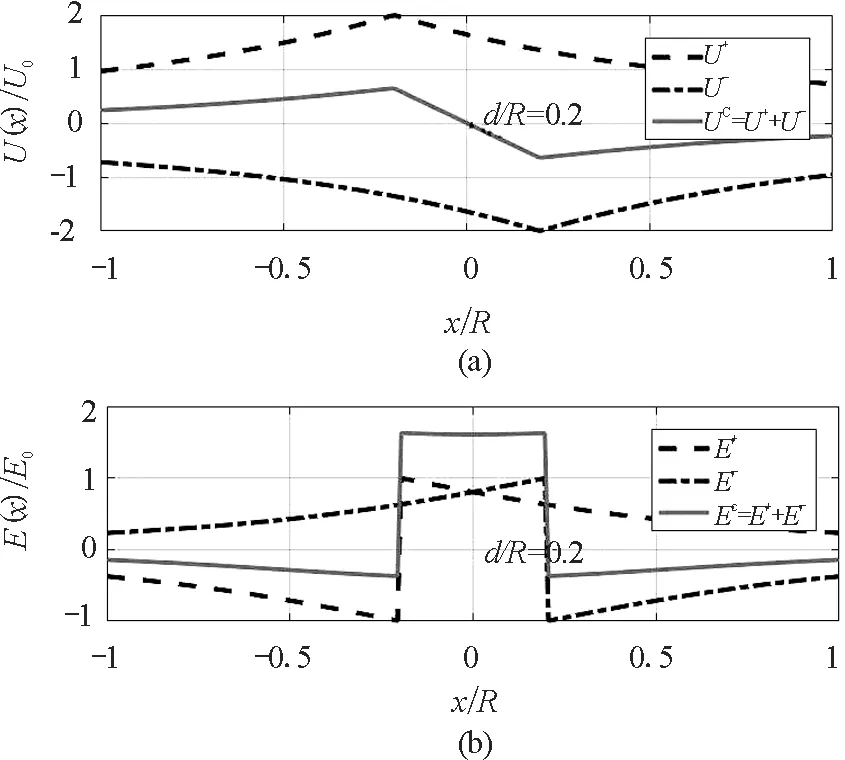
图4 均匀等量异号带电圆板共轴线上的电势和场强

半距d取0.1R到0.25R的值，间隔为0.05R，如图5（a）所示，不论两板之间的距离如何，两板之内的电势UC（x）都是经过原点的单调下降的曲线，接近于直线；当d不同时，“直线”的斜率稍有不同.如图5（b）所示，两板之间的场强EC（x）在x=0是极小值；两板距离越小，板内的场强EC（x）就越大，也越均匀，板外的场强就越小.当d=0.1R时，板内的场强线又高又平；当d=0.25R时，板内场强线明显变低且下凹，连中垂线上都不是匀强电场，其他地方就更不是匀强电场了.

图5 不同距离d的轴线上的电势和场强

由式（28）可得轴线上场强均匀系数K随两板距离d的关系如图6所示.

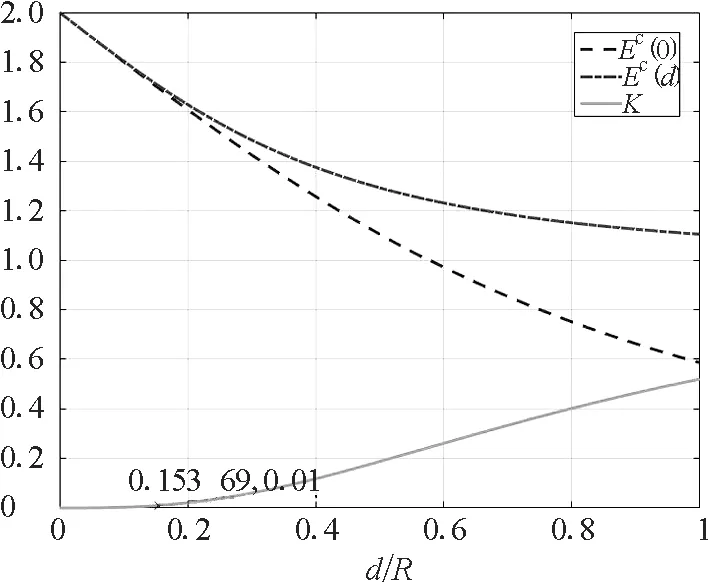
图6 轴线上的场强及场强的均匀系数和分界点

由图6可知，中心的场强EC（0）和内边缘的场强EC（d-）或EC（-d+）都随着半距d的增加而减小，均匀系数K随着半距d的增加而增加.当K=1%=0.01时，利用M ATLAB可以计算d=0.153 7R.在图5中，当d=0.1R时，K=0.29%，所以板内场强曲线十分水平；当d=0.2R时，K=2.08%，所以板内场强曲线略显下凹.可见只有当两板距离很小时，均匀带电圆形薄板两板之间在轴线上的电场才能当作匀强电场，d=0.153 7R是1%均匀性的分界点.

6 结束语

利用M ATLAB可以帮助我们学习和研究电学问题.检验公式是否正确的一种简单方法就是画出曲线.通过曲线，发现式（1）和式（2）只在x＞0的区间才成立.通过慎密演算，就能得到在全部区间都成立的公式.

均匀带电圆形共轴薄板在轴线上的电场是一个典型问题，比较容易计算，可是，即使在轴线的电场也不是均匀的.电场的均匀性并不是指某一个场强值，而是指电场大小的分布范围.用均匀系数可以衡量电场的均匀性.均匀带电的平行薄板在轴线上的场强也可以用同样的方法研究其轴线上的均匀性.