材料力学剪力、弯矩图“一笔画”
○ 文/杨树宇
在材料力学中,计算梁弯曲时的内力,并绘制剪力、弯矩图,是力学教学的重要内容,是对梁进行强度计算和刚度校核的依据,同时又是后续课程的很重要的基础知识。但对大多数学生来说却是一个难点,在计算截面内力和应用简捷法、叠加法绘制内力图时经常出现错误,而使内力图成为力学教学和学习中的一个“瓶颈”,且简捷法、叠加法绘制时需要分段,然后逐段进行分析、绘制,计算过程相对复杂。针对这个问题,通过几年来的研究和教学实践,笔者尝试使用了一种更直观、更简捷的描绘内力图的方法,并称之为“剪力、弯矩图‘一笔画’”。
之所以称之为“剪力弯矩图‘一笔画’”,是受智力游戏“一笔画”中不断笔、不重复地从起点到终点画出完整图形的启发。笔者通过研究发现剪力、弯矩图的绘制中也有这样“一笔画”的规律可循。要一笔绘制出一个完整的剪力或弯矩图,就要分析清楚各段图线的线型,各段图线的连接及图线的起、终点等 问题。
一、“一笔画”理论分析
(一)剪力、弯矩图的线型
由我们已知的知识可知,剪力、弯矩图图线是分段绘制出的,在各段中图线有平行于轴线的直线、斜直线、二次抛物线等基本线型。据微分关系及微分关系的几何意义可知,剪力、弯矩图线型与荷载分布形式有紧密联系:当梁段上无荷载分布时[q(x)=0],剪力图图线是一条平行于杆轴线的直线、弯矩图图线是一条斜直线;当梁段上有均匀分布的荷载时[q(x)=常数],剪力图图线是一条斜直线、弯矩图图线是一条二次抛物线(如图1)。这样内力图在各梁段上的线型就确定清楚了。
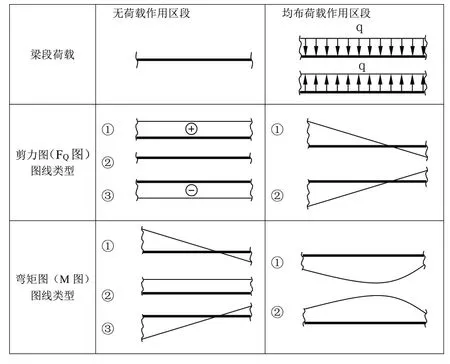
图1
(二)剪力、弯矩图各段图线的连接
当各段的图线得到了确定后,接下来的问题就是如何“一笔”连接各段线条。这就要搞清楚图线分段的依据,及剪力、弯矩图图线中的连续与突变。
首先,图线的分段是以梁段上荷载作用的突然变化为分段依据的。而图线是连续还是突变,就要视荷载情况来分析了:当梁上荷载由无荷载变为有均布荷载时,剪力、弯矩图图线将改变线条的形状或方向,但线条是连续的,不发生突变;当有集中荷载F作用时,剪力图发生突变,弯矩图连续;当有集中力偶m作用时,剪力图不受影响,弯矩图发生突变,如图2所示。
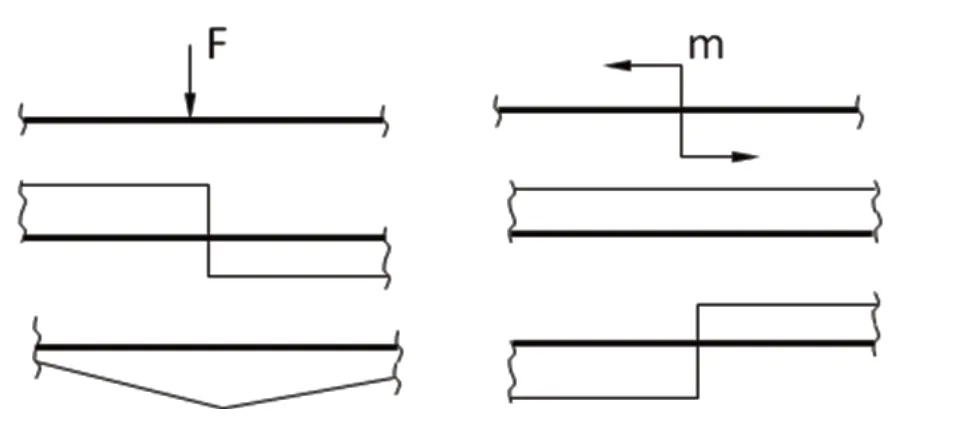
图2
突变时:截取突变截面处的微段分析,如图3所示。
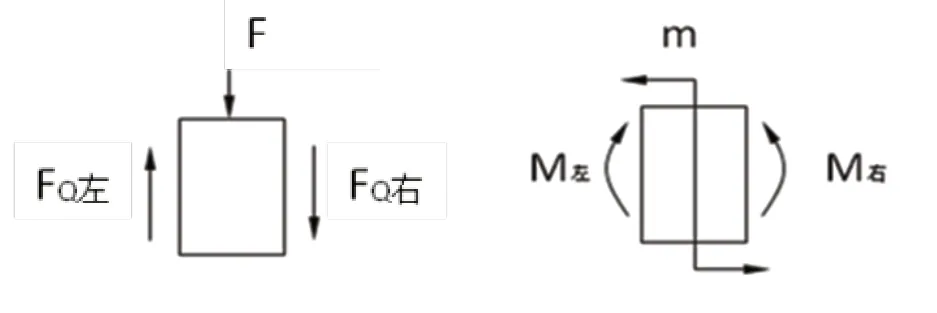
图3
得: FQ右=FQ左-F, M右=M左-m
可见突变值的大小为集中力F或集中力偶m的大小。反应在图形上,剪力图和弯矩图在此处的横坐标不变,纵坐标变化F或m,此时连接前后两段图线的线段垂直于轴线,恰好为图线的纵标线,而图形在纵标线的连接下被完整的一笔连起来。
据内力计算可知,绘剪力图时,如果绘制顺序是从左向右,那么剪力图突变的方向正好与荷载的作用方向相同,即遇向下的集中荷载,剪力图向下突变,反之向上;绘弯矩图时,弯矩图突变的方向也与荷载的作用方向相关:遇逆时针外力偶作用时,弯矩图向上突变(在土建工程类材料力学中,弯矩图绘制时,基线上方为负),反之向下。
因此剪力、弯矩图在梁段上的图线可据荷载作用情况,逐段连续绘制。当无突变时,连续绘制;当有突变时,以纵标线连接连续绘制。(纵标线绘制的方向和大小由外力来定)。
(三)图线的起、终点
前面分析了图线绘制过程中可一笔绘制,那么图线从哪起笔,又从哪收笔呢?对梁的整个图线来说,其杆件端点内力对应的纵标应为图线的起点,但杆件端点内力的纵标值也与外力有关。其纵标线的绝对值的大小,在剪力图中恰好为杆端竖直方向集中力的大小;在弯矩图中恰好为外力偶矩的大小。此处的纵标线可视为杆端外力外侧的截面内力为零,遇有外力作用后产生突变(如图4)。此纵标的性质与上述“剪力、弯矩图图线中的连续与突变”性质一样。那么,杆端外力外侧内力为零,即纵标起点为零。同理终点处纵标也为零。所以在“一笔画”绘制内力图时,“一笔画”的起点为基线的起点,同时终点也恰为基线的终点。
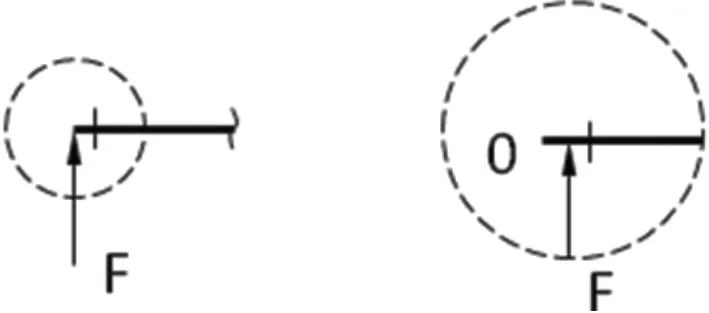
图4
二、剪力图“一笔画”方法
1.计算支反力。
2.确定基线。
3.绘图线。一般为从基线左端起笔开始向右连续绘图(称“从左向右绘图法”)。
绘剪力图图线方法:从基线左端起笔,向右连续绘制首尾相接的图线段,各种线段为:
(1)遇集中荷载(包括支反力),则沿集中荷载指向,向上或向下绘垂直于基线线段,线段长为集中荷载大小;
(2)遇无荷载梁段,绘平行于基线的图线;
(3)遇向上(或向下)均布荷载,绘斜向上(或斜向下)直线,斜直线的起点与终点差值为对应梁段上均布荷载的合力值(q·a)。
这样,一条图线从基线左端起连续绘至右端时,图线应回到基线,完成“一笔画”。再标出各控制点处纵标值及纵标线、符号、图名、单位等,至此剪力图绘制完毕。则整条图线为从基线左端起笔连续绘制线段至基线右端止的图线。概括为一句话:“剪力图线走向与荷载方向一致,连续绘制”。(说明:如果从右向左绘制时,图线走向与荷载方向相反)。
举例说明:绘如图5所示梁的内力图(支反力的计算过程略)。例题剪力图(FQ图)说明:如 图5(b)。
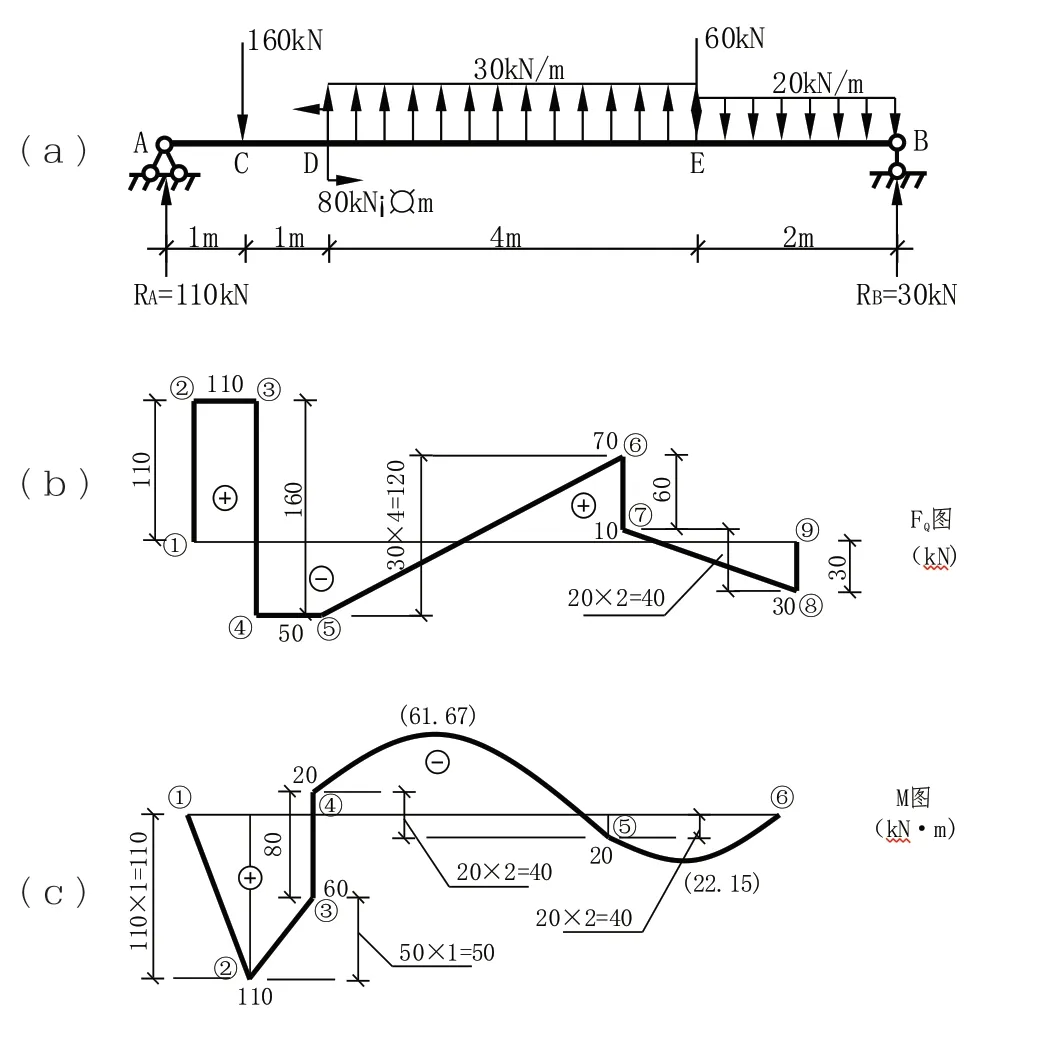
图5
如图所示,FQ图图线共有八段图线一笔连接而成:
①-② 段:遇竖直向上集中荷载RA=70kN ——图线竖直向上画70,纵标由0至70;
②-③ 段:无荷载梁段——水平直线,纵标70;
③-④ 段:遇竖直向下集中荷载120kN——图线竖直向下画120,纵标由70至70-120=-50;
④-⑤ 段:无荷载梁段——水平直线,纵标-50;
⑤-⑥ 段:遇向上均布荷载,合力大小为30×4=120kN——图线斜向上画直线,起点与终点差值为120,纵标由-50至-50+120=70;
⑥-⑦ 段:遇竖直向下集中荷载60kN——图线竖直向下画60,纵标由70至70-60=10;
⑦-⑧段:遇向下均布荷载,合力大小为20×2=40kN——图线斜向下画直线,起点与终点差值为40,纵标由10至10-40=-30;
⑧-⑨ 段:遇竖直向上集中荷载RB=30kN ——图线竖直向上画30,纵标由 -30至-30+30=0,且回到了基线。
三、弯矩图“一笔画”方法
比起剪力图的绘制,弯矩图计算较复杂,数据不易得出,所以不宜直接采用“一笔画”来绘弯矩图。但借助剪力图以面积法来计算,同样也可方便的“一笔”绘出弯矩图。方法如下:
1.确定基线。
2.绘图线。同绘剪力图一样,画弯矩图时一般也是从左向右连续绘制。
注意:因是借助剪力图来绘制,而剪力图中反映不出集中力偶的作用,所以绘弯矩图时应结合荷载图中的集中力偶作用,不能丢掉。
绘弯矩图(M图)图线的方法:从基线左端起笔向右连续绘制首尾相接图线段,各种线段为:
①遇力偶作用,据该力偶矩使向下段梁产生正弯矩(或负弯矩),向上(或向下)绘垂直于基线线段,线段长为该力偶矩大小;或据遇逆时针外力偶作用时,弯矩图向上突变,反之向下来判断图线绘制方向。
②遇剪力图为等于0直线段,则绘平行于基线 线段;
③遇剪力图为正水平线段(与基线构成一矩形),则绘斜向下直线;如剪力图为负水平线段,则绘斜向上直线;绘出的斜直线起点与终点差值为此段剪力图与基线构成的矩形面积大小;
④遇剪力图为斜直线时,对应弯矩图为二次曲线,二次曲线的凸向与斜直线斜向一致,即斜向上直线对应向上凸二次曲线,反之对应向下凸二次曲线。此二次曲线两端差值△M计算如下:
设剪力图斜直线的起点、终点剪力值为a、b,斜直线对应基线段长度为L,则对应二次曲线起点、终点差值△M=(b+a)L/2(注意a、b取代数量)。如果计算△M>0,则二次曲线终点在起点下侧,反之如△M<0,则终点在起点上侧。另,在二次曲线段内如有极值,则需另外计算。
如上述方法,一条图线从基线左端起连续绘制至右端时,应回到基线,然后标出各控制点纵标值、纵标线、符号、图名、单位等,至此剪力图绘制完毕。
概括一句话来表达:“弯矩图图线走向与剪力图面积大小及符号一致,连续绘制”。
(说明:如果图线从右向左绘制时,图线走向与剪力图面积符号相反。)
例题M图说明:如图4(c)。
如图所示,弯矩图图线共有五段图线一笔连接而成:
①-② 段:正水平剪力图线段,面积70×1=70——图线从基线起,斜向下画直线,纵标由0至70-0=70。起、终点差值70;
②-③ 段:负水平剪力图线段,面积50×1=50——图线斜向上画直线,纵标由70至70-50=20,起、终点差值20-70=-50;
③-④ 段:集中力偶(使下梁段产生负弯矩)40kN·.m ——图线竖直向上20-40=-20,纵标由20至20-40=-20,起、终点差值-20-20=-40;
④-⑤ 段:斜向上剪力图线段面积 △M=〔70-(-50)〕×4/2=40——图线为二次曲线,终点在起点下侧40,起终点差值20-(-20)=40;
⑤-⑥ 段:斜向下剪力图线段面积 △M=(-30+10)×2/2=-20——图线为二次曲线,终点在起点上侧20的,纵标由20至20-20=0,起终点差值0-20=20,回到基线。
上述绘制剪力图、弯矩图的方法,可以认为是面积法计算截面内力与简捷法绘内力图的一种有机结合,是将计算过程融合到图形的绘制当中。特别是这种方法有一显著的特点,即:由基线起,到基线止,这样,在绘图完毕后即可检验出图形绘制是否正确,这有助于我们准确地绘制出内力图。通过教学实践,学生们普遍感到这种方法易学易会,简便快捷,是一种较实用的解题方法。

