任意大于2的偶数都是两素数之和

陆沪僧

(湖南省醴陵市陆顺机械厂 412200)

一、素数在数轴上的排列规律

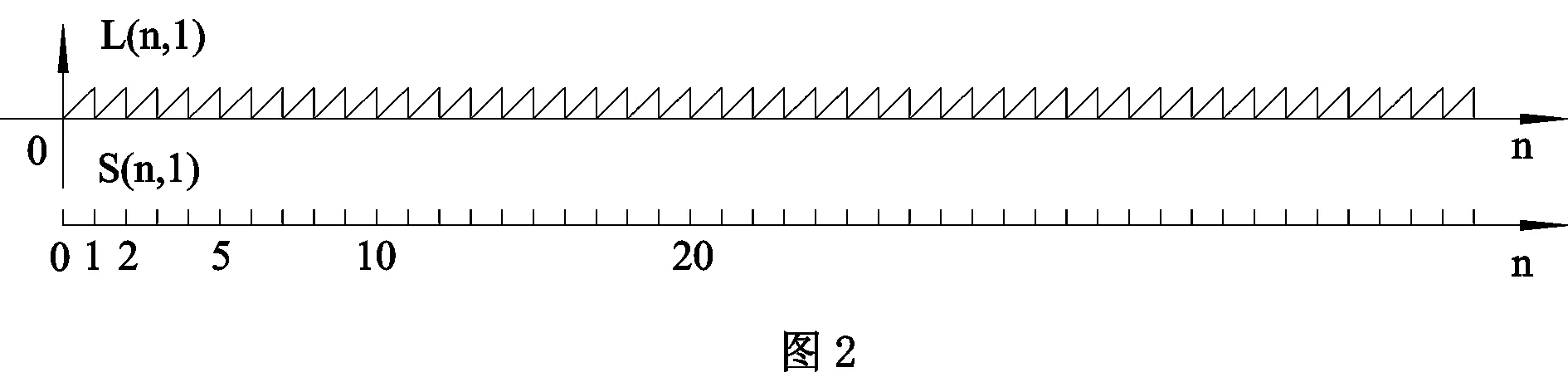
1.S(n,p1p2…pr)数轴

在数轴的正方向上，去掉最小素数p1=2的一切整数倍数的点，再在余下的整数点中去掉下一个素数p2=3的一切整数倍数的点，…，这样依次做下去,直到去掉pr的一切整数倍数的点,称这样的数轴为S(n,p1p2…pr)数轴.

将S(n,p1p2…pr)数轴上留下来的整数点称为L点.

2.L(n,p1p2…pr)图线

表示S(n,p1p2…pr)数轴L点位置及规律的图线，叫L(n,p1p2…pr)图线.

引进定义和定理

定义：设n是任意实数，[n]表示小于n的最大整数，{n}表示n-[n]，有：[n]=n-{n}.

过数轴上任意点n作数轴的垂线nn0，交L0线于n0，交Q(n,pi)图线于n1，有：

因为S(n,p1p2…pr)数轴，是在数轴上，减去前r个素数的一切整数倍数的点，加上在减去前r个素数的一切整数倍数的点时重复减去的点;…一直到加上或者减去所有r个素数的一切整数倍数的点，而形成的数轴；

所以L(n,p1p2…pr)图线，是在表示数轴的图线上，减去表示前r个素数的一切整数倍数的点的图线，加上表示在减去前r个素数的一切整数倍数的点时重复减去的点的图线;…一直到加上或减去表示所有r个素数的一切整数倍数的点的图线，而形成的图线.

先求出这些图线：

数轴图线，即L(n,p0)图线.

L(n,p0)图线的斜率为1；周期为1.

一元图线，即Q(n,pi)图线.

每次取出一个素数的一切整数倍数的点的位置及规律的图线，这些图线应该减去；

以Q(n,5)图线为例：如图3.

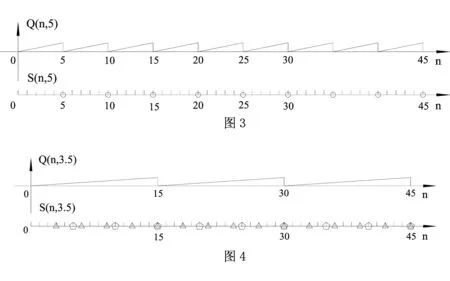
二元图线，即Q(n,pipj)图线.

去掉pi和pj的一切整数倍数的点时，重复去掉的点位置及规律的图线，这些图线应该加上.

以Q(n,3.5)图线为例：如图4.

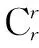
根据L(n,p1p2…pr)图线形成的规律，有：

L(n,p1p2…pr)图线=数轴图线-一元图线+二元图线-…+(-1)rr元图线.

以素数序号r=3为例，画出L(n,2.3.5)图线，如图5

同理，可以得到所有的L(n,p1p2…pr)图线.

而且，L(n,p1p2…pr)图线的J点与S(n,p1p2…pr)数轴的L点一一对应,

因此，S(n,p1p2…pr)数轴L点的位置及规律，能够用L(n,p1p2…pr)图线表示.

3.L(n,p1p2…pr)图线的特点.

(1)L(n,p1p2…pr)图线的J点与S(n,p1p2…pr)数轴的L点一一对应；

(2)L(n,p1p2…pr)图线原点对称，对称原点为n×p1p2…pr(n=0,1,2,…)；

(3)L(n,p1p2…pr)为周期图线，它的周期为p1p2…pr；

二、素数在对折数轴上的排列规律

1. S2(n,p1p2…pr)数轴

将S(2n,p1p2…pr)数轴沿整点n对折，对折后的S(2n,p1p2…pr)数轴形成的双层数轴，称为S2(n,p1p2…pr)数轴.

将S2(n,p1p2…pr)数轴从0到折点n的一段称为上轴，大于n的一段称为下轴.

在S2(n,p1p2…pr)数轴上,如果存在这样的点：这点的上轴是S(2n,p1p2…pr)数轴的L点；下轴也是S(2n,p1p2…pr)数轴的L点,这种上下L点对齐的点称为L2点.

L2点上轴L点的数值与下轴L点的数值之和为偶数2n.如图6

2. L2(n,p1p2…pr)图线

表示S2(n,p1p2…pr)数轴L2点位置及规律的图线，叫L2(n,p1p2…pr)图线.

同理，L2(n,p1p2…pr)图线=对折数轴图线-一元图线+二元图线-…+(-1)rr元图线.

画出对折数轴图线、一元图线、二元图线、…、r元图线.

对折数轴图线：L2(n,p0).

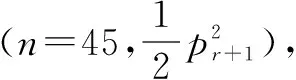
Q2(n,pi)图线：

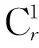
Q2(n,pi)图线分两种情况：(1)2n能被pi整除，(2)2n不能被pi整除；

(1)2n能被pi整除：

(2)2n不能被pi整除：

Q2(n,pipj)图线：

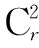
因为Q2(n,pipj)图线是在去掉pi和pj的一切倍数时，重复去掉的点的位置及规律的图线，而pi和pj的一切倍数的点与Q2(n,pi)图线和Q2(n,pj)图线的J点一一对应,所以Q2(n,pipj)图线的J点是Q2(n,pi)图线的J点和Q2(n,pj)图线的J点的重合点；

Q2(n,pipj)图线的斜率是Q2(n,pi)图线的斜率×Q2(n,pj)图线的斜率.

以Q2(59,3.5)为例(n=59，p2=3，p3=5),如图10.

Q2(59,3.5)图线的J点是Q2(59,3)图线的J点和Q2(59,5)图线的J点的重合点.

Q2(59,3.5)图线的斜率是Q2(59,3)图线的斜率×Q2(59,5)图线的斜率.

因此，只要确定Q2(n,pi)的J点和Q2(n,pj)的J点的重合点的位置与Q2(n,pi)的斜率和Q2(n,pj)的斜率，Q2(n,pipj)的图形就能确定.

Q2(n,pipjpk)图线：

Q2(n,pipjpk)的J点是Q2(n,pi)的J点、Q2(n,pj)的J点和Q2(n,pk)的J点的重合点；

Q2(n,pipjpk)的斜率为Q2(n,pi)的斜率×Q2(n,pj)的斜率×Q2(n,pk)的斜率.

以Q2(59,3.5.7)为例(n=59，p2=3，p3=5，p4=7),如图11.

Q2(59,3.5.7)的J点是Q2(59,3)的J点、Q2(59,5)的J点和Q2(59,7)的J点的重合点；

Q2(59,3.5.7)的斜率是Q2(59,3)的斜率×Q2(59,5)的斜率×Q2(59,7)的斜率.

同理，可以得到所有的：对折数轴图线、一元图线、二元图线、…、r元图线.

因为，L2(n,p1p2…pr)图线=对折数轴图线-一元图线+二元图线-…+(-1)rr元图线，

所以，通过以上这些图线的运算，可以得到所有L2(n,p1p2…pr)图线.

以L2(59,2.3.5.7)为例(n=59，p1=2，p2=3，p3=5，p4=7)说明图线的画法：如图12.

L2(59,2.3.5.7)由下列图线形成：

L2(59,2.3.5.7)=L2(59,1)-Q2(59,2)-Q2(59,3)-Q2(59,5)-Q2(59,7)+Q2(59,2.3)+Q2(59,2.5)+Q2(59,2.7)+Q2(59,3.5)+Q2(59,3.7)+Q2(59,5.7)-Q2(59,2.3.5)-Q2(59,2.3.7)-Q2(59,2.5.7)-Q2(59,3.5.7)+Q2(59,2.3.5.7).

L2(59,2.3.5.7)的斜率

3.L2(n,p1p2…pr)图线的一般形式

根据L2(n,p1p2…pr)图线的特点：

(1)L2(n,p1p2…pr)图线的J点与S2(n,p1p2…pr)数轴的L2点一一对应；

(2)L2(n,p1p2…pr)图线是有间断点的单线图线；

(3)因为折点n被所有去掉的素数整除，余数的种类有p1p2…pr种，所以，L2(n,p1p2…pr)图线有p1p2…pr种；

(4)L2(n,p1p2…pr)图线原点对称，对称原点为n×p1p2…pr(n=0、1、2、…)；

(5)计算图线的斜率时，凡是含pi的所有斜率，斜率的表达式中都含有分母为pi的分数：

如果折点n能被pi整除，计算斜率时，含有pi的所有分数的小数部分，分子都是1，

如果折点n不能被pi整除，计算斜率时，含有pi的所有分数的小数部分，分子都是2，

(当折点n能被pi整除时，ti=1；当折点n不能被pi整除时，ti=2)；

g.因为：t1恒为1，t2-tr=1或者2，所以，L2(n,p1p2…pr)图线的斜率种数为2r-1.

所以，L2(n,p1p2…pr)图线有一般形式：如图13.

三、任意大于2的偶数都是两素数之和

因为L2(n,p1p2…pr)图线是周期图线，所以Cr有最大值.

如果求得Br-Cr的最小值，就可以得到L2(n,p1p2…pr)图线的J点的最少个数.

下面求：(1)素数序号r为自变量，Cr的最大值；

(2)素数序号r为自变量，Br+1-Br的最小值和Br的最小值.

1.素数序号r为自变量，Cr的最大值

首先，求Ar+1的最大值.

在L2(n,p0)上依次去掉p1、p2、…、pr的一切整数倍数的点，形成L2(n,p1p2…pr)图线；

(1)如果在去掉pi的一切整数倍数的点时，去掉的J点中包含Ai点，则又会产生Ai+1点；

(2)如果在去掉pi的一切整数倍数的点时，去掉的J点中不包含Ai点，则Ai点变成Ai+1点.

L2(n,p1p2…pr)图线的0到Ai+1段，在去掉p1p2…pr的一切整数倍数的点时，同时去掉了每次形成的A1、A2、…、Ar；L2(n,p1p2…pr)图线的L0线上只有0与Ar+1.如图15.

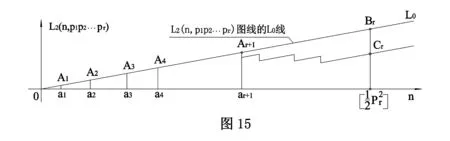
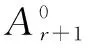
得出：素数序号r为自变量，Cr的最大值不会大于r+1.

在平面直角坐标上，令x轴为素数序号r，y轴为Cr，

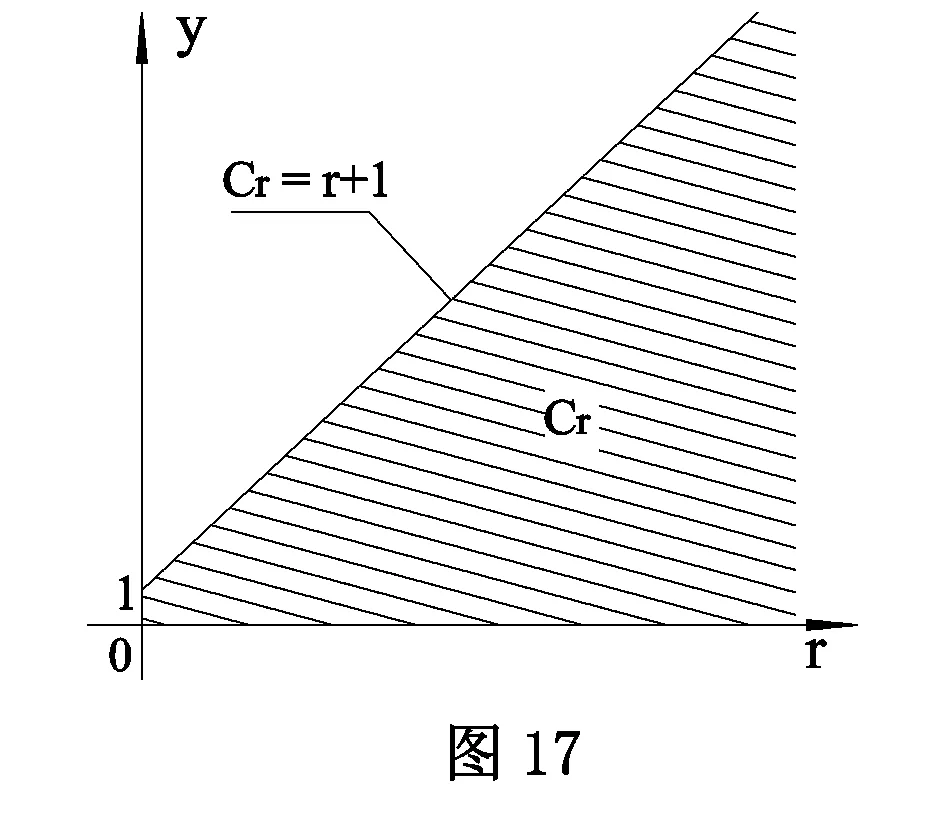
则Cr的取值范围在直线Cr=r+1，斜率为1的斜线的下方，如图17.

2.素数序号r为自变量，Br+1-Br的最小值和Br的最小值.

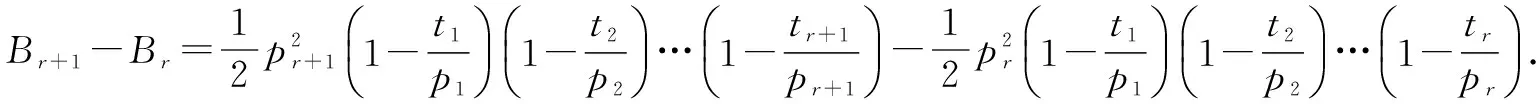
化简上式，提取公因式Br，在化简过程中：

(1)除t1=1以外，令其余ti=2时，则L2(n,p1p2…pr)图线的斜率最小，所计算的Br最小；

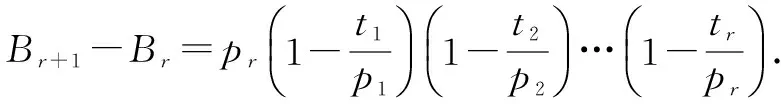
因为当r﹥12时，上式将会乘以大于1的数，

所以，当r﹥12时，Br+1-Br﹥1.

这时，求Br的值就变成求B12的值.

所以，当素数序号r=12时，B12>20.

有：r=12时，B12>20；r>12时，Br+1-Br﹥1.

在平面直角坐标上，令x轴为素数序号r，y轴为Br.

根据以上结论，L2(n,p1p2…pr)图线的Br值的取值范围在斜率为1，过点(12,20)的斜线(Br=r+8)的上方.如图18.

3.比较图17和图18，将Br=r+8和Cr=r+1两条斜线放在同一坐标系中，它们是两条永不相交的平行线，Br的最小值比Cr的最大值至少大于7.如图19.

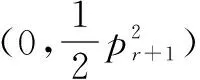
因为

S2(n,p1p2…pr)数轴的L2点与L2(n,p1p2…pr)图线的J点一一对应，所以，当r>12时，S2(n,p1p2…pr)数轴上至少有7对素数之和为偶数.

小于1369的偶数用作图的方法逐一进行证明，也可以用凑数的方法直接证明.

结论：任意大于2的偶数都是两素数之和.

参考文献：

[1]陈景润.初等数论[M].北京：科学出版社，1978.