在测量体验中深刻理解度量思想

摘要：数学概念是数学的“细胞”，也是构成数学体系的“基石”。小学生数学核心素养的发展离不开数学概念的支撑，而概念的建立又是在一次次数学活动体验中累积而成的。数学活动体验在深化理解概念，促进学生的深度学习方面功不可没，它是培养学生敏捷的思维能力、提升核心素养的重要载体。教学本课时可立足学情，创设情境，引发度量兴趣;测量体验，引发冲突，认识统一度量单位的必要性;围绕核心问题，组织探究，进入理性思维;更新测量方法，深入辨析，领悟数学高阶思维;设计练习活动，促进知识的内化与外拓，提升数学核心素养五个方面，让学生深刻理解度量思想。

关键词：数学概念;测量体验;度量思想;深入

数学概念是数学的“细胞”，也是构成数学体系的“基石”。小学生数学核心素养的发展离不开数学概念的支撑，而概念的建立又是在一次次数学活动体验中累积而成的。数学活动体验在深化理解概念，促进学生的深度学习方面功不可没，它是培养学生敏捷的思维能力，提升核心素养的重要载体。

“课桌有多长”是北师版《义务教育教科书·数学》二年级上册第六单元“测量”里的内容。图形的测量体现了度量意识、空间观念、应用意识的发展，测量的关键是选取恰当的测量单位对图形进行度量，使学生在测量的实际操作过程中积累数学活动经验，感受数学思想，进而从量的角度挖掘图形中所隐藏的数学性质，培养学生的度量意识。这些隐性的知识、思想是教学中最为关键的因素，是形成学生空间观念的基础，也有利于学生数学素养的长远发展。下面就以“课桌有多长”为例，谈谈怎样通过数学活动体验积累活动经验，促使度量思想走向深入。

一、立足学情，创设情境，引发度量兴趣

二年级的学生已经有了两次关于长度单位的直接经验（即一年级上册的“比长短”和“教室有多长”的自选单位测量），在这两次测量活动中，学生对长度概念有了一些直观认识，并会用“长、短、一样长、短一些、长得多、有几个什么那么长”等词语来形象地描述物体的长度特征。从“课桌有多长”开始，学生要学习定量的方法，即比较准确地描述一个物体究竟有多长。

针对学生的年龄特点和认知规律，我设计了这样的教学情境：“请同学们仔细观察桌面，工厂师傅要为我们的桌面铺一张合适的塑料垫板，我们要为工厂师傅提供哪些数据呢？”一个好的情境，评判的标准就是看它是否能唤起兴趣、激活认知、产生冲突、激发创造。那好的情境从哪里来？它来自教师通过对教材的深度挖掘，制定出的教学目标;来自教师对班级不同学生认知特点的充分了解;来自让学生先行的课堂预习活动的反馈;来自对学生想法的倾听、感知和捕捉;来自教学实践、反思所生成的教学智慧……基于此，这个教学情境的设计无疑是成功的，它从学生所熟悉的现实情境出发，以测量垫板的长和宽的长度作为驱动任务，唤醒了学生已有的生活经验，学生的测量需求一下子就被激發了出来，课堂氛围顿时变得很活跃。

二、测量体验，引发冲突，认识统一度量单位的必要性

度量单位是几何度量中的重要内容，是基于现实生活的需要而逐渐形成的，是人类祖先的伟大发明，也是前人智慧的集中体现。在测量中选择合适的度量单位是关键，度量单位的多样性和统一性反映了人类测量活动的发生、发展的历程，反映了测量的本质。因此，在测量体验中带领学生回溯人类的认知发展过程，经历数学知识的“再创造”过程是十分必要的，因为它是指导个体认知发展的最佳方法。根据测量产生和发展的历史，根据学情，在正式学习“统一单位度量”之前，我设计了运用“非标准长度单位测量”这一环节，即自选单位测量，目的就是引发冲突，进而让学生感受建立统一度量单位的必要性。

师：怎样测量课桌的长边与短边的长度？

生：用尺子量，用数学书量，用文具盒量，用手量，用橡皮量……

师：用手量，就要引进一个概念“拃”。什么是“拃”？

生：就是拇指和中指之间的长。

师：正确。下面以小组为单位进行实际测量。要求先商量好你们小组选择什么测量工具，再实际测量，最后以喜欢的方式把测量结果填在表格里。（学生活动时，教师巡视指导。对于测量中没有做标记或没有一个挨一着个测量的学生，教师应及时帮助提醒减少误差。）

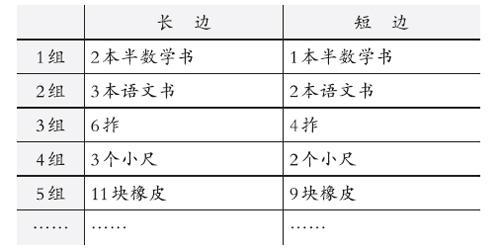
学生小组合作测出课桌长度后，我组织学生进行了交流，并在黑板上呈现出各组的测量结果。

然后，引导学生观察发现：“为什么测量同一物体的长度，得到的结果不同？”“这么多的测量结果，把哪一种报给工厂师傅，比较合适呢？”这一问，犹如一石激起千层浪，它激活了学生的思维，让学生发现，正是度量的标准不统一，测出的结果才会五花八门。把这样的结果送给工厂师傅，工厂师傅肯定不知所措，必然是无从下手。这样，建立统一的度量单位这一共识便呼之欲出。这种数学活动经验，正是在“做”与“思”的过程中积淀出来的，学生经历了一次数学化的过程，从实际问题中抽象出数学问题，“必须使用统一的度量工具才能得到统一的结果”，从而引出测量的核心概念——厘米。

三、围绕问题，深入探究，转向理性思维

尺子是每个学生必配的学习用具，二年级学生虽然年龄小，但对尺子已经很熟悉，他们常在手工课上用尺子画直线，还有一部分学生已经知道了可以用尺子测量长度。但1厘米到底有多长，学生还不是很清楚，课堂上需要通过大量的测量和实践活动，让学生充分去感知，从而建立表象。所以在接下来的教学活动中，我以核心问题“1厘米有多长？”引领学生层层开展探究体验活动，深入理解“厘米”这个概念，逐步实现长度单位由动作思维向理性思维的转变。

（一）借用小尺、微课，从静态上认识长度单位“厘米”

师：数学王国有个好朋友，他可以帮助工厂师傅准确地做课桌。（微课出示尺子）仔细观察，你看到了哪些信息？

生：有数字0、1、2、3、4……有许多线，有长有短，还有字母cm。

师：（微课演示介绍各部分知识）数字是按从小到大的顺序排列的，三种长度不同的竖线叫刻度线，0刻度在尺子最左边，表示起点，数字指向几就是几厘米，尺子上的“cm”是常用的长度单位，它也可以用文字“厘米”表示。（板书：长度单位——厘米cm）

师：那1厘米有多长呢？

师：仔细看，0刻度到1之间的长度就是1厘米，也可以说是1cm。即1厘米=1cm。（板书：1厘米=1cm）

（二）借助手指、小木棍从动态上认识长度单位“厘米”

师：首先，请用食指在尺子上找到刻度“0”，再用拇指找到刻度“1”，这中间的长度就是1厘米。请大家比量一下，看看1厘米有多长。

师：请拿出提前发给大家的一段1厘米长的小棍，用你的拇指和食指夹住，再把小棍轻轻地抽出来，拇指和食指之间的缝隙大约是1厘米。

师：请大家闭上眼请想一想，1厘米有多长？用手势比量下，再对照尺子比量一下，看你表示的是否准确。

（在这些活动体验中，静态的“1厘米”就会在学生的心中逐渐变得“生动”“鲜活”起来。）

（三）在找一找，比一比的活动中，实现由动作思维向理性思维的转变

首先，引导学生在小尺上找还有哪段也是1厘米长。

生：刻度2～3，刻度3～4，刻度5～6……

师：你发现了什么？

生：一大格就是1厘米。

（让“1厘米”的知识告别死板的说教，不固化学生的思维，让学生的思维灵活起来。）

其次，引导学生从熟悉的物体或自己的身体上找，哪些物体的长度大约也是1厘米。

生：手指一节的长度大约1厘米，数学教材的厚度大约1厘米，笔尖的长度大约1厘米，图钉的长度大约1厘米，橡皮的厚度大约1厘米……

这一环节有效地帮助学生把抽象的长度单位，变成看得见、摸得着的，具体可感的东西，有利于“厘米”表象的建立。

最后，引导学生在小尺上找几厘米，并引发思考，弄清几厘米的含义。

师：请大家在尺子上再找一找，从哪儿到哪儿是2厘米长？从哪儿到哪儿是3厘米长？从哪儿到哪儿是5厘米长？

师：它们为什么是2厘米？3厘米？4厘米？

生：因为它有2个1厘米，所以是2厘米;因为它有3个1厘米，所以是3厘米……

师：你发现了什么？

生：从0到第几个大格就是几厘米。

生：用后面大刻度数减前面小刻度数，得几就是几厘米。

生：是几厘米，这几厘米里就有几个1厘米。

这一环节的体验，不仅拓宽了学生对“厘米”这个度量单位的理解，还实现了长度单位由动作思维向理性思维的转变。更重要的是，在这些体验中积累下的经验，能促进学生估测意识的形成和估测能力的提高，对他们今后的学习也大有益处。

核心问题如何引领学生进行探究？不是“强制引领”，而是以“问题串”的形式，即引导学生为解决核心问题而自主生成一系列的子问题，以不断地“问题—思考—分享”循环往复的形式使探究活动层层开展，使思维得以不断地拓展、深入。在探究中，一定要保证学生有足够的时间进行独立思考，要让他们充分发表见解，引发思维碰撞，最终形成解决问题的策略。

四、更新方法，深入辨析，领悟数学高阶思维

在学习测量方法时，我对学习方式进行了大胆的革新，将“量一量铅笔的长度”设计成了“辨析四种测量方式的正误”，渗透了“测量的起点不同，但数格子的方法不变”这一“变中不变”的数学思想，引领学生的思维向深处延伸，如同“剥笋”般由表及里，更深入地理解了知识的本质。我是这样操作的——

先让学生“估一估这支铅笔有多长”，引导学生学会估量的方法：用1厘米长的手势去比量，看看铅笔有幾个1厘米长，它就是几厘米。

再组织学生用尺子动手自主操作进行实际测量“这支铅笔到底有多长”。

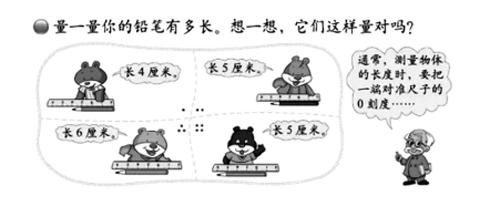
在测量的过程中，学生可能会出现教科书中呈现的几种情况。

于是，我继续引导学生结合实际测量辨析这四种测量方法的正误，在观察、对比、判断、辨析中掌握正确的测量方法，沟通数一数与算一算两种方法的本质联系。

师：请大家来当评委，哪只小熊的测量方法是对的？

生：第1种测量方法是错的，因为物体没有和0刻度对齐。

生：第2种的测量方法是对的。因为和0刻度对齐了，而且正好有5个大格，所以铅笔长5厘米。

师：测量的时候，物体和尺子一定要放平，一般情况下，让物体的一端和尺子的0刻度对齐，看物体的另一端对着刻度几，就是几厘米。但是，如果是断尺，那又该怎么测量呢？

生：第3种测量方法是对的，但结果是错的，在数格子的时候，不该算上第一大格。

生：第4种测量方法是对的，算得也对，1和6相差5厘米，即6-1=5，正好是5个大格，所以是5厘米。

师：没错。用断尺测量的时候，可以从某一数字开始量起，用大刻度减去小刻度，得几就是几厘米。

师：刚才的铅笔长5厘米，有的同学用数格子的方法，有的同学用算一算的方法，你更喜欢哪种方法呢？

生：我喜欢算的方法，简单准确;数的方法，容易马虎，而且费时。

在学会测量的基础上，还可以再引导学生利用尺子画一条长4厘米的线段，内化所学的知识。学生掌握了知识和技能不是教学的终点，我们还应在对问题的深入探究中，让学生学习思维的方法，特别是质疑和批判性的思维。对核心问题的适度拓展，有利于学生批判性地看待新知，并引发深入思考，加深他们对知识概念的理解，促进其高阶思维的发展。发展思维能力是学习数学的重要任务，实践表明，恰当的变式和拓展更有利于学生的思维向深处发展，更有助于建模。

五、设计练习，实地测量，促进知识的内化与外拓

我是这样设计练习题的——

1.用小尺测量课桌的长边，巩固并内化所学知识。

2.用小尺还可以测量什么？（橡皮、课本、电视机，等等，让学生明确厘米可以作为较短物体的长度单位。）

3.如果测量教室的长度、操场一圈的长度、从学校到家的长度用小尺合适吗？

我并未拘泥于回顾本课所学知识或收获的思路，而是着眼更广阔的视角，引领学生展望长度单位的学习线索：测量课桌、书本、电视机等的物品可以用厘米作单位来测量，测量教室、操场等更大的距离就要以米、千米等单位来测量了。这样，将学生的思维引向后续的学习，便于长度单位作为一个整体存储于学生的认知系统中，实现知识的内化、思维的融通，为学生的可持续发展奠定了基础。

参考文献：

[1]刘克臣. 基于整体把握视角下的小学数学度量教学[J]. 中小学教学，2019（4）.

[2]王智明. 小学数学中度量性概念的教学思考[J]. 新课程研究，2016（1）.

（责任编辑：杨强）