非线性偏积分微分方程紧隐显BDF方法的误差分析
兰海峰,肖飞雁,张根根,朱 瑞
(广西师范大学 数学与统计学院,广西 桂林 541006)
本文主要研究一类非线性抛物型偏积分微分方程的数值解法,其方程的基本形式为
(1)
式中(x,t)∈[a,b]×[0,T],初边界条件定义为
u(x,0)=φ(x),a≤x≤b,
(2)
u(a,t)=ua(t),u(b,t)=ub(t), 0≤t≤T。
(3)
偏积分微分方程的数值解法已有许多研究,如有限差分方法[1-6]、谱方法[7-11]以及有限元方法[12-16]等。目前,针对方程中的非线性项,学者们主要通过隐显格式(IMEX)或线性化方法进行处理,其原因在于全显式时间离散方法对时空步长要求高,全隐式时间离散方法则在每一个时间点都要迭代求解一个非线性隐式方程组,而隐显格式或线性化方法则避免了求解非线性代数方程组,从而减少计算量并提高计算效率。如Shampine等[17]提出一种求解刚性扩散反应偏微分方程的隐显方法;而后,Hundsdorfer等[18]对具有一般单调性和有界性的线性多步方法进行了隐显格式的推广;Avazzadeh等[1]借助梯形公式使积分线性化表示;Xiao等[19]、Zhang等[20-21]考虑了隐显单支方法求解几类时滞微分方程,克服解的时间(偏)导数具有间断性所导致的困难,获得了方法的收敛性结果;Li等[22]、Zhang等[23]则利用泰勒展开等方式对非线性的非齐次项进行了相应的处理。
本文在空间方向采用紧致差分方法,时间方向采用隐显BDF方法对方程(1)~(3)进行离散,积分项则利用梯形数值求积公式求解,最终构造出一种高效且稳定的数值方法,称为紧隐显BDF方法。本方法只依赖所求节点的临近点,故最终可得系数矩阵为三对角阵的线性代数系统,并使用Thomas算法求得最终结果。为此,设方程的解析解u(x,t)关于方程(1)~(3)都是充分光滑的,即u(x,t)∈C6,4([a,b]×[0,T]),设fμ和fν分别是定义在0-邻域上对函数f第1和第2个元素的一阶偏导,0>0。可以设
(4)
(5)
(6)
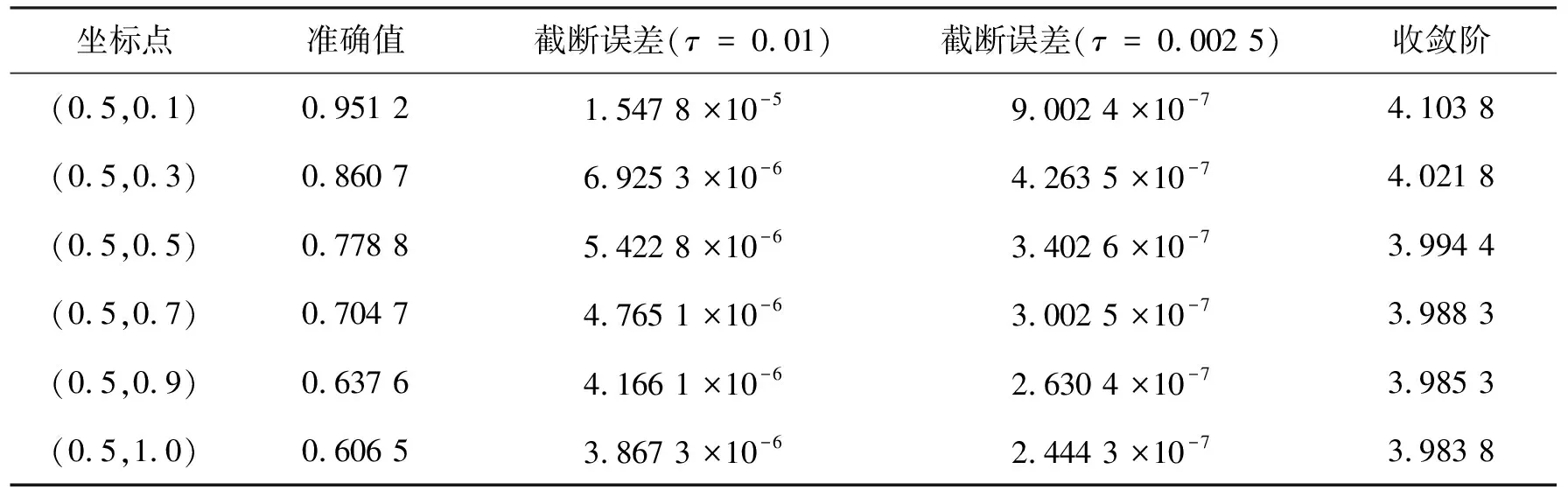
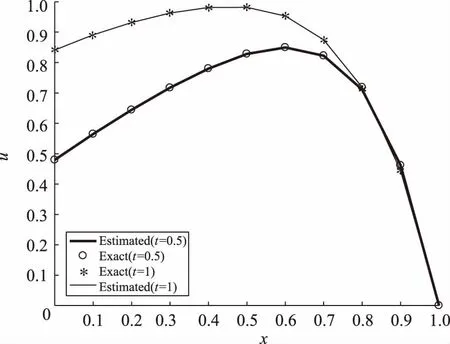
式中:gγ表示g函数中关于第3个元素的一阶导数;π1={x∈(a,b),0 本文安排如下:第1章得出求解方程(1)~(3)的紧隐显BDF方法及相应的局部截断误差;第2章给出相应数值格式的矩阵形式,验证其三对角性,并分析了可解性;第3章分析紧隐显BDF方法的收敛性;最后,在第4章给出数值算例以验证数值格式的准确性和有效性。 (7) 先引入一个常用结果。 引理1[23]若存在p(x)∈C6[xi-1,xi+1],则 式中ω∈(xi-1,xi+1)。 在式(7)的基础上,考虑在节点(xi,tk+1)处的离散方程,可得 (8) 由泰勒展开可知 (9) (10) 对式(8)两边同时使用算子A,可得到紧差分的数值格式 (11) 利用引理1可得 (12) 再将式(9)、(10)、(12)代入式(11)中,得 (13) 式中 将已知初边值条件(2)~(3)对应改写为 (14) (15) (16) 定理1假设条件(4)~(6) 成立,则系统(15)~(16)的局部截断误差满足 (17) 式中:1≤i≤M-1;1≤k≤N-1。 (18) 其中系数矩阵定义如下 A,B都是M-1阶矩阵,定义在RM-1的列向量有U=(u1,u2,…,uM-1)T,以及 式中k≥1。事实上,矩阵A是对角占优矩阵,所以是非奇异的,故方程(18)存在唯一解。 设定义在Ωh上的网格函数空间V={v|v=(v0,v1,…,vM),v0=vM=0},对任意v,ω∈V,其内积与范数定义如下 引理3[23]对任意v∈V,可得 即 (19) 接下来,用数学归纳法对收敛性定理进行证明。将式(19)中的项拆分讨论,对左边第1项有 (20) 利用离散的格林公式,可以将式(19)中的左边第2项进行估计, (21) 对右边第1项,利用赫尔德不等式可得 (22) 对于右边第2项,可以进行如下估计 (23) 将式(20)~(23)带入式(19),得 将上述不等式两边同时乘以2τ,并对k求和,可得 再利用引理2的Gronwall不等式,上式可转化为 最后,应用引理3,得 由归纳法原理,定理得证。 本章将给出数值算例以验证算法的准确性和有效性。由式(17)可知,计算uk+1的值还需用到uk以及uk-1的值。事实上,只需提供k=1层,即时间第1层的值即可。为保证空间上仍为2阶收敛,利用泰勒展开,设存在ηi∈(t0,t1),使得 则时间上第1层的节点信息可表示为 式中φ″(xi)是函数u对x的2阶导函数并带入了t0的值,t0=0使得f中第2项的值为0。 在实际验算过程中,程序的计算运行时间均在3 s内,这确保了算法的高效性。 例1根据方程(1)~(3)的设定,考虑如下方程 此方程的解析解为u(x,t)=e-xt。表1给出了同一空间位置上不同时间点的准确值,而后给出了τ=0.01与τ=0.002 5条件下的截断误差。可以看出,网格越细,所得误差越小,当空间层取点步长减半时,其误差减少了1/16,验证了收敛可达4阶。 表1 例1的数值结果 当m与n的分割为10×100时,例1的近似解的图像如图1所示;图2给出了同等分割下近似解与真解的误差情况;图3展示了t=0.5与t=1时近似解与真解的情况。 图1 例1所求近似解的值(m=10,n=100) 图2 例1所求近似解与真解的误差(m=10,n=100) 图3 t=0.5与t=1时近似解与真解的对比 例2考虑式(1)~(3)具有初始条件 u(x,0)=(1-x6)sinx,0≤x≤1, 与边界条件 u(0,t)=sint,0≤t≤1;u(1,t)=0, 0≤t≤1, 并在非齐次项中有g(x,s)=ex+tu(x,s), 及 的抛物型偏积分微分方程。 此例的解析解为u(x,t)=(1-x6)sin(x+t)。表2详细给出了在空间点x=0.5处部分时间节点上的准确值、收敛阶以及τ=0.01与τ=0.002 5条件下的截断误差。可以看出,最终的收敛阶仍然接近4阶。 表2 例2相关的数值结果 图4展示了例2在m与n的分割为10×100的条件下所得的近似解的图像;图5给出了同等密度分割下近似解与真解的误差;图6给出了t=0.5与t=1时的近似解与真解对比情况。 图4 例2所求近似解的值(m=10,n=100) 图5 例2所求近似解与真解的误差(m=10,n=100) 图6 t=0.5与t=1时近似解与真解的对比 本文给出一种求解非线性抛物型偏积分微分方程的高阶数值格式,此格式在空间上采用4阶紧差分方法,在时间上基于2阶隐显BDF方法进行离散,并利用梯形求积公式处理了非齐次项中的积分项;而后证明了此方法的收敛性;最后,数值实验的结果表明此方法具有良好的精度,收敛阶能够达到预估,验证了方法的高效性和稳定性。今后考虑结合交替方向等技巧将此结果推广至2维和3维情形。1 紧隐显BDF方法格式




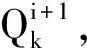


2 紧隐显BDF方法的矩阵形式


3 收敛性分析




4 数值算例







5 结束语

