含Ornstein-Uhlenbeck过程的随机SIS传染病模型

李淑一, 韦煜明, 彭华勤

(广西师范大学 数学与统计学院, 广西 桂林 541006)

自古以来, 传染病的流行给人类造成了巨大的危害。公元6—19世纪间, 鼠疫在全球发生了3 次大流行, 波及亚、欧、美和非洲60多个国家, 死亡人数达千万。自1817年以来, 霍乱已经在全球发生7次大流行, 死亡人数也以千万计[1]。传染病给人类造成的损失远远超过历史上所有战争的总和。随着科学的发展, 许多对人类有严重威胁的传染病得到了有效控制，然而人类与传染病的斗争还远远没有结束, 因此, 传染病的防治仍是当前世界各国公共卫生工作的重要内容之一。充分了解传染病的传播模式和疾病控制理论, 对人类与传染病斗争有很大的帮助。

近年来, 许多学者通过建立数学动力学模型来分析和解决传染病引起的各种现象和问题[2-8], 为传染病防控策略的研究提供可靠的理论依据。例如，没有持久免疫力的性传播疾病和细菌疾病，对于这类疾病，人类从易感状态开始, 感染之后经过一些周期之后又重新回到易感状态。这类疾病是典型的SIS模型[9-11]。文献[12]给出如下确定性传染病模型

(1)

由于环境的随机多变性, 人们常常引入白噪声来建立随机传染病动力学模型。例如，γ→γ+σdB(t), 确定性系统(1) 就转化成随机系统

(2)

除了这种线性的白噪音扰动，还有另一种方法。本文将研究含有均值回复的随机传染病模型来讨论回复速率和波动强度对传染病的影响。假设参数γ满足均值回复过程[13-19]，即

dγ(t)=θ(γe-γ(t))dt+ξdB(t),

(3)

式中θ、ξ都是正数，θ是回复速率,ξ是波动强度。Dixit和Pindyck[20]在Financial-Economics理论中已经研究了均值回复过程。用伊藤公式计算式(3)，得

(4)

式中γ0:=γ(0)。计算得γ(t)的期望是

E(γ(t))=γe+(γ0-γe)e-θt。

(5)

γ(t)方差是:

(6)

式中B(t) 是标准布朗运动。因此式(4)可以写成如下形式

(7)

其中

(8)

将式(7)带入式(1)中得到如下随机微分方程

(9)

1 全局正解的存在唯一性

研究传染病模型的动力学行为的前提是系统是否有全局正解, 本章将证明系统(9)有全局唯一正解。

定理1对于任意给定初值(S(0),I(0))∈D, 系统(9)存在全局唯一正解(S(t),I(t))∈D(t≥0), 且概率为1, 即

证明显然系统(9)的系数满足局部Lipschitz条件, 并且存在局部解(S(t),I(t)),t∈[0,τe),τe是爆炸时间。欲证该解是全局的, 只需证τe=∞ a.s.。设η0>0且满足S(0)>η0,I(0)>η0。对任意η≤η0(η>0)，定义停时

τη=inf {t∈[0,τe):S(t)≤η,I(t)≤η},

V(S(t),I(t))=S-1-lnS+I-1-lnI。

显然V(S(t),I(t))是正定的。由伊藤公式得

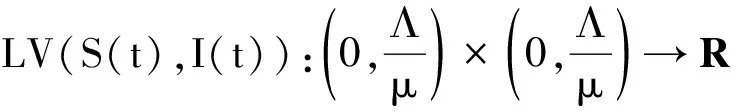
式中M是正常数。所以

对上式两端从0 到τη∧T求积分并取期望得

E(V(S(τη∧T),I(τη∧T)))≤V(S(0),I(0))+MT。

令Ωη={τη≤T}, 则P(Ωη)≥。对每一个ω∈Ωη, 由停时定义知，在S(τη∧T)和I(τη∧T)中至少有一个等于η, 可得V(S(τη∧T),I(τη∧T))≥η-1-lnη。所以

V(S(0),I(0))+MT≥E(χΩηV(S(τη∧T),I(τη∧T)≥(η-1-lnη),

式中χΩη是Ωη的示性函数, 当η→0,∞>V(S(0),I(0))+MT=∞,矛盾,所以τ0=∞ a.s.,即τe=∞, 局部解u(t)为全局解, 得证。

2 疾病的灭绝与持久

2.1 疾病的灭绝

记系统(9)的确定性系统(即ξ=0)的基本再生数为

系统(9)的基本再生数为

(10)

即传染病以概率为1灭绝。

证明用伊藤公式计算得

两边同时从0 到t积分得

所以

2.2 疾病的持久性

(11)

和

(12)

式中

(13)

证明用伊藤公式计算得

N(0)=N0=S0+I0为初值。

对固定ω∈Ω2∩Ω4∩Ω5,t≥T1(ω)，

3 回复速率和波动强度

(14)

则ρ严格单减，且

得证。

(15)

则ρ严格单增，且

得证。

由定理5知,ρ关于θ严格单增, 且θ→θ*时ρ趋于0, 即疾病灭亡。从生物学角度看，回复速率越小可抑制疾病, 当回复速率足够小时疾病灭亡。

4 数值模拟

5 总结