基于在线社交网络的JPS跳跃并行顶点采样方法

赵倩文

(浙江理工大学信息学院，浙江 杭州 310018)

0 引 言

在线社交网络(Online Social Networks， OSNs)从早期的概念化阶段慢慢地发展到交友和娱乐，整个发展过程中最重要的是将人们线下生活移至线上并且拉近了人们的距离,这使得虚拟的社交网络与现实的社交出现了很多的交集，成为一个社交的工具。

随着近几年OSNs的飞速发展，其受到全球各年龄阶层人们的欢迎。社交网络用户总数已达到三十多亿，占全球总人口的四成，数量极其庞大且持续地增长。OSNs的迅速发展也吸引了大量的研究人员去探究其背后的大数据隐藏的信息，研究课题也是多种多样[1]。

因为OSNs的数据庞大[2]，想要完整地分析需消耗大量的时间，同时有些数据集比较稀疏，尚且不能完整地处理[3]。研究人员在分析这些数据时遇到的挑战之一就是如何采集具有代表性的样本数据。所以需要设计一个有效的采样方法，采集一个属性接近原始数据集的小型代表性无偏见的样本,以供研究人员分析[4]。

研究OSNs的数据集时，将其看作一个拥有顶点和连接边的图来分析。将用户看作顶点，把用户之间的关系当作连接边，建模成一个社交图[5]。目前为止已经出现了多种顶点采样方法，可以用于OSNs数据样本的采集。宽度优先采样(Breadth-First Search， BFS)是一种比较常用的采样方法，但BFS的采样偏向于高度顶点，随机游走(Random Walk， RW)[11-12]不适用于断开的图并且偏向于高度顶点，蒙特卡罗随机游走(Metropolis-Hasting Random Walk， MHRW)和无偏延迟采样(Unbiased Delay， UD[4])方法依然不适合采样断开连接或松散连接的图[5]，信天翁(Albatross Sampling， AS)采样花费成本很大[14]。

1 蒙特卡罗随机游走

早期的很多文献都涉及在线社交网络的样本采集方法的研究[6]，也提出了很多有用的采样方法，但现有采样方法各有利弊。其中宽度优先采样是比较常用的，但是采样获取的样本偏向于高度顶点，并不能代表原始数据集[7]；而RW、MHRW、UD方法将节点选择问题公式化[8],却不适应于低连通社交图的采样。

MHRW采样方法就是基于RW方法提出的，一定程度上消除了样本顶点的偏差。当社交网络顶点连接良好时，MHRW方法可以很好地获得社交图的无偏样本。实现原理是根据给定的任意一个概率分布，构造一个以该分布为静态分布的马尔科夫链[3]，然后执行该马尔科夫链，达到收敛之后开始采样。MHRW方法与RW方法相同的是,下一样本顶点依然从当前顶点的邻居顶点中选择，不同的是,选择下一样本顶点时不是等概率的。MHRW采样过程中从v到w的转移概率表示为：

(1)

其中,v和w表示顶点，P表示从v转移到w的概率，kv和kw分别是顶点v和w的度数。从转移概率可以看出,MHRW采样过程中每个顶点的选择更倾向于低度顶点，这样就可能使低度顶点的自循环升高，陷入局部连通良好的区域，导致低度顶点过入样[13]。另一个不足之处在于该方法依然不能适用于低连通社交图的采样，因为MHRW方法获得的顶点仅在某一个连通子图中。

2 跳跃无偏并行顶点采样方法

2.1 采样方法基本思想

本文将在线社交网络建模为一个由用户顶点集合V和用户之间连接边集合E构成的社交图，表示为G=(V,E)，其中E集合的每条边都是未加权的[9]。而在线社交图分为无向图和有向图，对于无向图顶点的度数是连接的邻居顶点数，但是在采样有向图时需要给顶点的每条边添加一个标志着进出方向的属性将其转化为无向图再进行采样，针对指向顶点的边设为入度，指出的边设为出度。

下面基于MHRW采样方法，针对其较高的自循环率和不能适用低连通强度社交图的缺陷做出改进。首先提出一个双保险的跳跃策略以便提高采样时对全局顶点的公平性，且对于不同连通强度的社交图都是可以避免困于局部连接良好的区域，同时降低了顶点的自循环概率；其次添加一个顶点缓存区，采样过程中以一定概率在此处随机选择与当前顶点度数相同的顶点作为下一顶点，可以降低全局跳跃的成本；最后多路并行采样加快了样本采集的效率，尽可能在最短时间采集一定数量的顶点。

顶点缓存区D是一个初始为空的区域，随着采样的进行把采集到的顶点的所有邻居顶点按照顶点度数排序后添加进去，形成一个独立的区域。并行意味着采样不是一条主线进行到底的，而是多路并行采样互不干扰。

跳跃无偏并行顶点(Jump unbiased Parallel vertex Sampling， JPS)采样方法引入了2个跳跃参数α与β，其中α控制着采样过程中从顶点缓存区内随机选取与当前顶点相同度数的下一顶点的概率，而β控制着采样过程中从全局顶点V中随机选取下一顶点的概率。

由于D中顶点是随着采样的进行逐渐添加的，可知采样的前期D并没有足够的顶点数量，要保持一个较大的β值提高算法在初期的全局搜索能力,以致加快了算法的后期收敛速度[15]，从而采集到全局中其他顶点且能尽快增加顶点缓存区顶点数量，而在采样中后期D中顶点足够支撑采样的跳转时可以设置较小的β值降低跳转成本，因此可得：

(2)

其中,s表示采样过程中采集的顶点数，S表示需要的样本总数量。设置2个不同区域跳跃参数α与β的优点在于降低了受困于局部连接良好的区域的可能性，以便采集到性能更接近原始连通图的小型代表性样本。

α定义为静态值，规定了顶点在缓存区中的跳跃概率，在Twitter数据集中进行5次采样绘制不同α值的样本顶点平均度分布图如图1所示。

图1中横坐标为α的值，纵坐标为样本平均度，黑色线Ori为原始Twitter社交图的平均度。图1(a)为(0，1)范围内α的取值对采集的样本平均度的影响，可看出最优的α值在(0，0.2)之间，图1(b)为(0，0.2)范围内α的取值对采集的样本平均度的影响，由于图1(b)中5次采集的样本平均度与原始网络平均度差距较小，但α在(0.1,0.2)范围内时采样平均度高于原始平均度，所有从(0.05,0.1)选取的α值均可，本文以α=0.08进行采样。

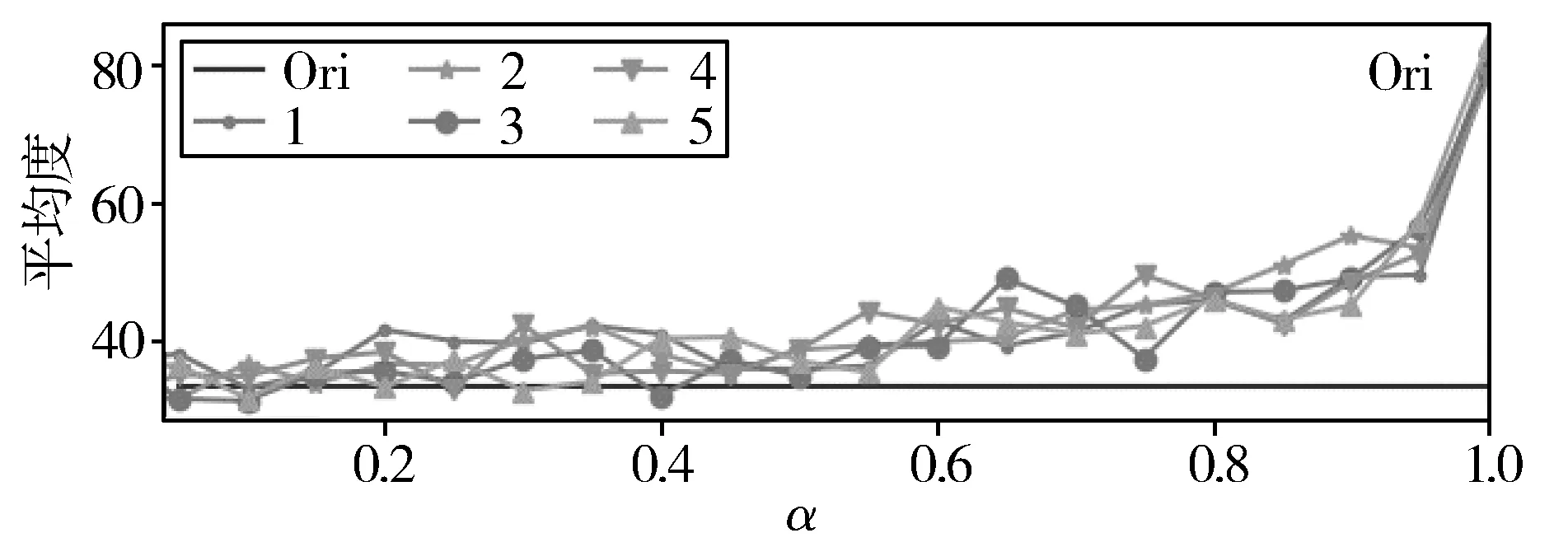
(a) α在(0,1)范围内取值

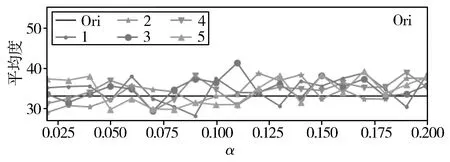
(b) α在(0，0.2)范围内取值

2.2 JPS采样工作流程

上面确定了跳跃机制中顶点缓存区D中的跳跃概率α=0.08，全局跳跃概率，下面是JPS采样方法的代码实现过程。

算法1JPS Sampling

1 Input: GraphG=(V,E)

2 Select 10 random vertexvfrom theVas the initial node

3 Addvto thes

4 Node jump area dictD←empty

5 While stopping criterion not met Do

6 Foriin neighbors ofv

7 Addito theD

8 While stopping criterion not met Do

9 Forvins(-11:-1)

10 Select nodewuniformly at random from neighbors ofv

11 Generatep1,p2,p3from uniform distributionU(0,1)

13 Addwto thes,v←w

14 elifp2<βthen

15 Selectarandom vertexufrom theV

16 Adduto thes,v←u

18 Stay atv

19 else

20 Selectdfrom dictD, whilekv=kd

21 Adddto thes,v←d

22 end if

23 end while

24 end while

25 Output: The set of sample verticess

2.3 JPS采样的无偏见性

JPS采样方法中下一样本顶点w的选择取决于当前顶点v。w可能是v的邻居，可能是与v相同度数的顶点，还可能是从全局社交图中随机选择的顶点。因此JPS方法采样过程可以建模为马尔可夫链，并且从当前顶点v到下一顶点w的概率是：

(3)

其中，v和w表示顶点，P表示从v转移到w的概率，kv和kw分别是顶点v和w的度数,而α是顶点缓存区D中的选择概率,取值为0.08,β为全局社交图中顶点的选择概率。

2.4 JPS采样的度分布

公式(3)完整地概括了JPS采样方法的实现原理，因为JPS采样方法是基于MHRW方法提出的，所以也可以构造一个静态分布的Markov Chain链使其能够进行无偏采样。双重跳跃降低了顶点的自循环概率，增加了全局顶点的入样概率，改善了现有采样方法无法适用于连通性低的网络。网络度分布是评估网络中不同度数顶点数量的一个评价标准，能够直观地展示在线社交网络中顶点的度数分布情况。下面针对Twitter数据集采样评估JPS采样方法采集的样本度分布图，如图2所示。

图2 Twitter中各采样方法的度分布

从图2可以看出，JPS采样方法获取的样本顶点平均度基本与原始Twitter数据集的网络度分布一致。

3 评估实验

第2章解决的问题是如何设计采样算法才能更高效地从一个大规模的在线设计网络数据集中获取一个与原始数据集性能属性相符的样本数据顶点。本章根据网络性能绘制顶点属性分布图，验证JPS采样方法所采集样本的各个属性[3,5,7]都更加接近于原始社交网络数据集，是符合要求的小型代表性样本顶点网络。一个数据集的属性有很多，所以对其的评价标准也是多种多样，在选择评价标准时，并不是越多越好，所以不需要对所有属性进行比较，本文仅使用较为常用的一些网络统计量。往年的研究表明，类似于网络顶点平均度、度分布、同配性等网络统计量[17-22]足够代表大部分评价标准。本文主要使用网络的平均度、顶点更新率、度分布P(k)以及收敛性对JPS采样方法与现有的MHRW、BFS、AS、UD等采样方法进行评估。

为了更公平地评估各采样方法获取样本的优劣，评估时选择了连通强度不同的Twitter和Epinions数据集，2个数据集的基本信息如表1所示。

表1 数据集的基本信息

表1中强连通分量表示有向图中最大连接子图的顶点数的值[23]。

3.1 样本网络的平均度

分别对Twitter和Epinions数据集进行采样，绘制样本顶点的平均度分布图如图3所示。

图3 样本顶点平均度

图3中，横坐标表示采集的样本顶点数量，纵坐标表示样本平均度，使用黑色线Ori来表示原始数据集的平均度。从图中可以看出不同的采样方法分别应用于Twitter和Epinions数据集时获取的样本顶点平均度变化情况。从图3(a)和图3(b)可以看出，样本平均度最接近于原始数据集平均度的采样方法为JPS，UD次之，AS与MHRW方法获取的样本平均度基本相同，BFS采集样本的平均度浮动较大、不够稳定，RW采集的样本偏向于高度顶点。

3.2 顶点更新率

顶点更新率(Ps)是衡量采样效率以及自循环的评价指标，更新率越高说明采样过程中采集到重复顶点的概率越低，同时也表明JPS采样方法更有效地跳出局部连通良好的区域并且降低了顶点的自循环概率。下面分别在Twitter和Epinions数据集中使用不同采样方法，进行样本顶点更新率的比较，绘制分布图如图4所示。

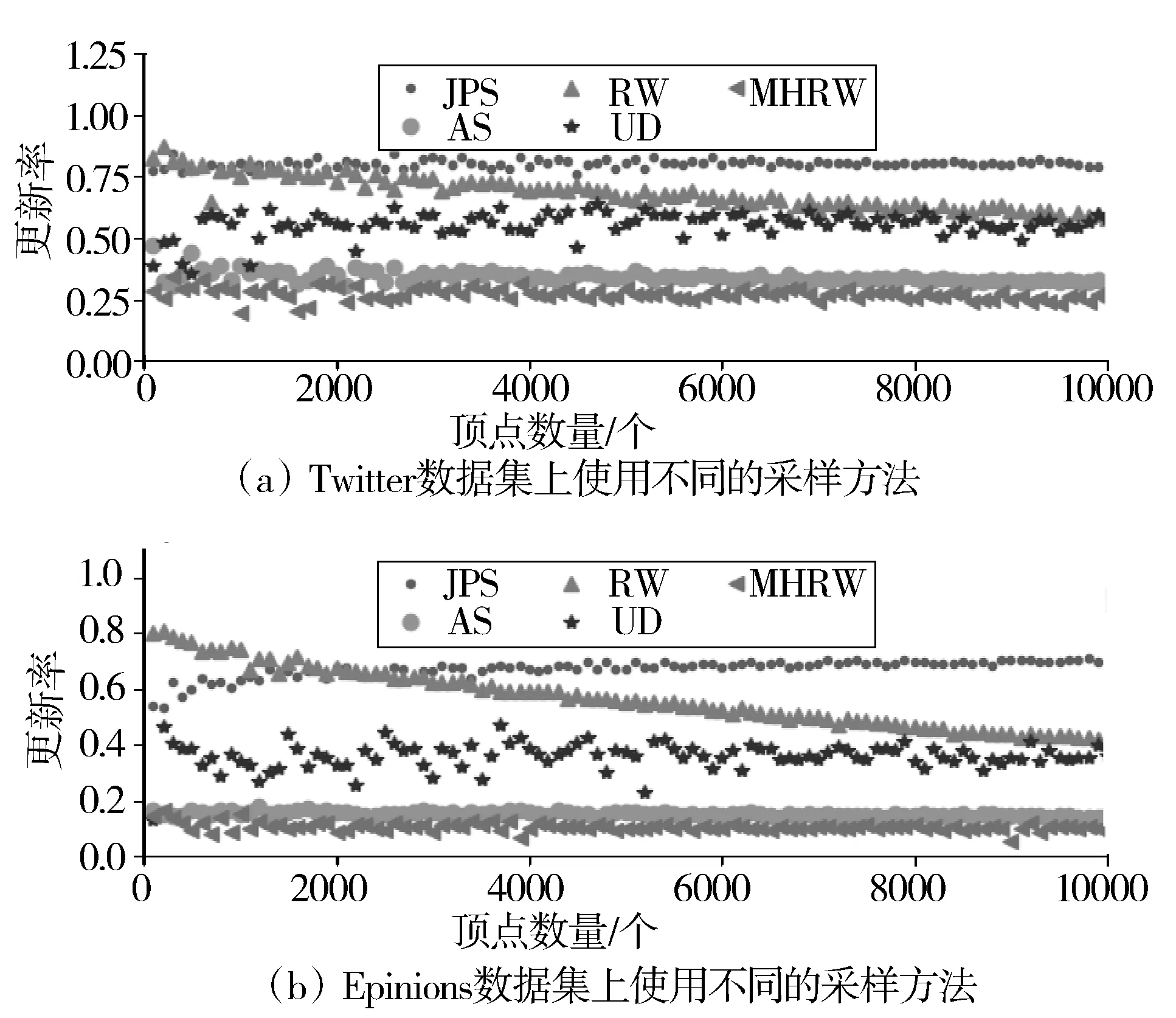
图4 样本顶点更新率

图4横坐标表示采样顶点数量S，纵坐标表示更新率Ps。从图中可以看出，无论在Twitter还是Epinions中，更新率比较高的是JPS和RW采样方法。但从图4(b)可以明显看出，RW采样方法不稳定，随着需要的样本数量S的增加，顶点更新率一直在降低。主要原因在于RW没有跳跃机制，容易受困于连通良好的网络子区域，当采样顶点数量增加时，就会过度采集重复顶点。综上，JPS采样方法相较于其他采样方法来说顶点更新率更高且更加稳定。

3.3 网络的度分布

图2展示了JPS采样方法应用于高连通的Twitter数据集中采集的样本度分布，而在低连通的Epinions数据集上进行采样，采集的样本度分布图如图5所示。

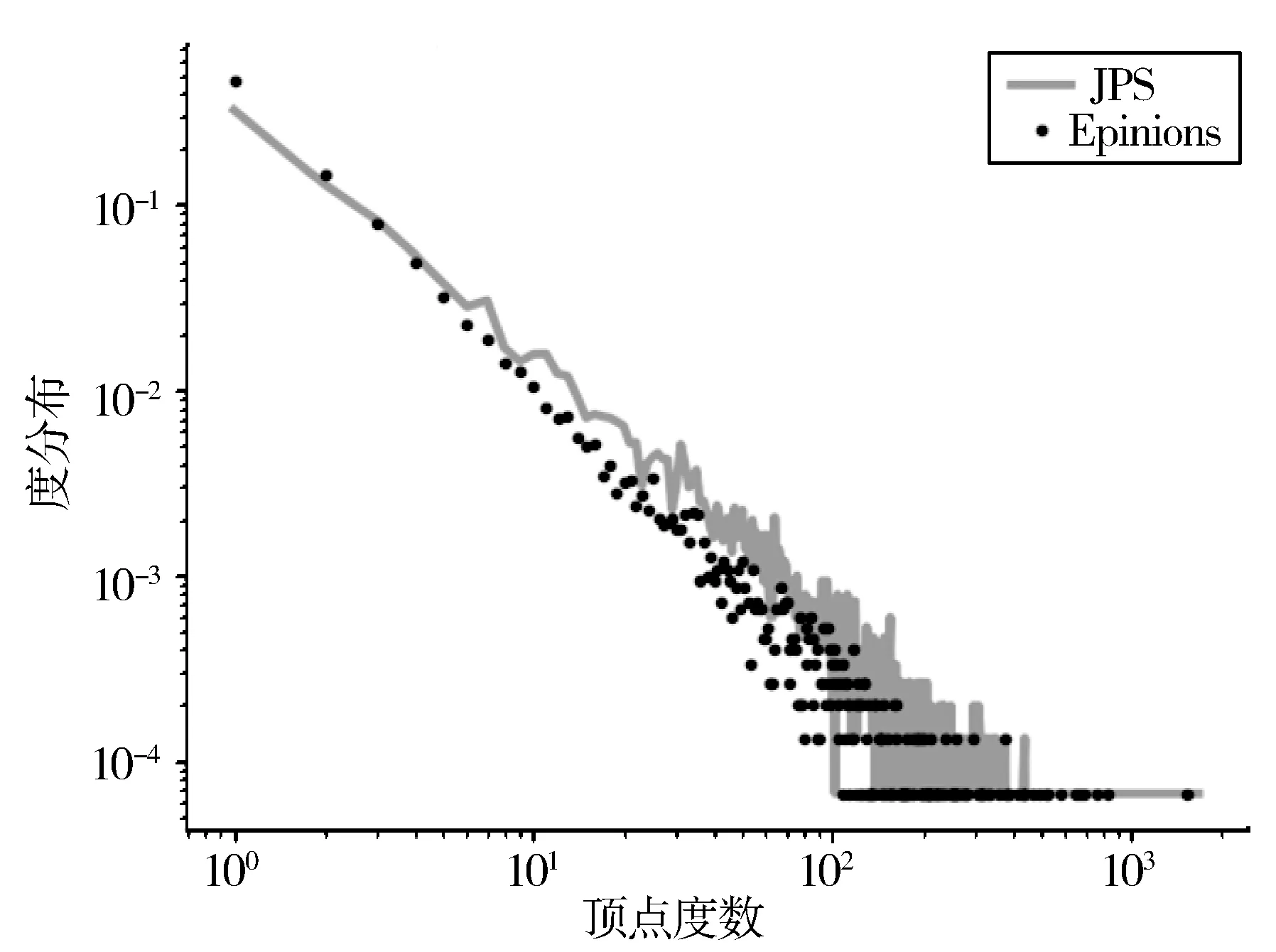
图5 Epinions中各采样方法的度分布

从图5可以看出，JPS采集的样本度分布依然近乎与Epinions原始数据网络度分布相同。由此可知，无论是高连通的Twitter还是低连通的Epinions的数据集中，JPS采样方法与原始网络的度分布都很接近，能很好地适用于不同连通强度的网络。

3.4 采样方法的收敛性

为了更公平地评估各种采样方法的性能，在Twitter数据集下使用MCMC诊断测试中广泛使用的Geweke诊断方法，绘制了MHRW、UD、AS和JPS采样方法的收敛曲线，如图6～图9所示。

图6 MHRW采样方法的收敛性

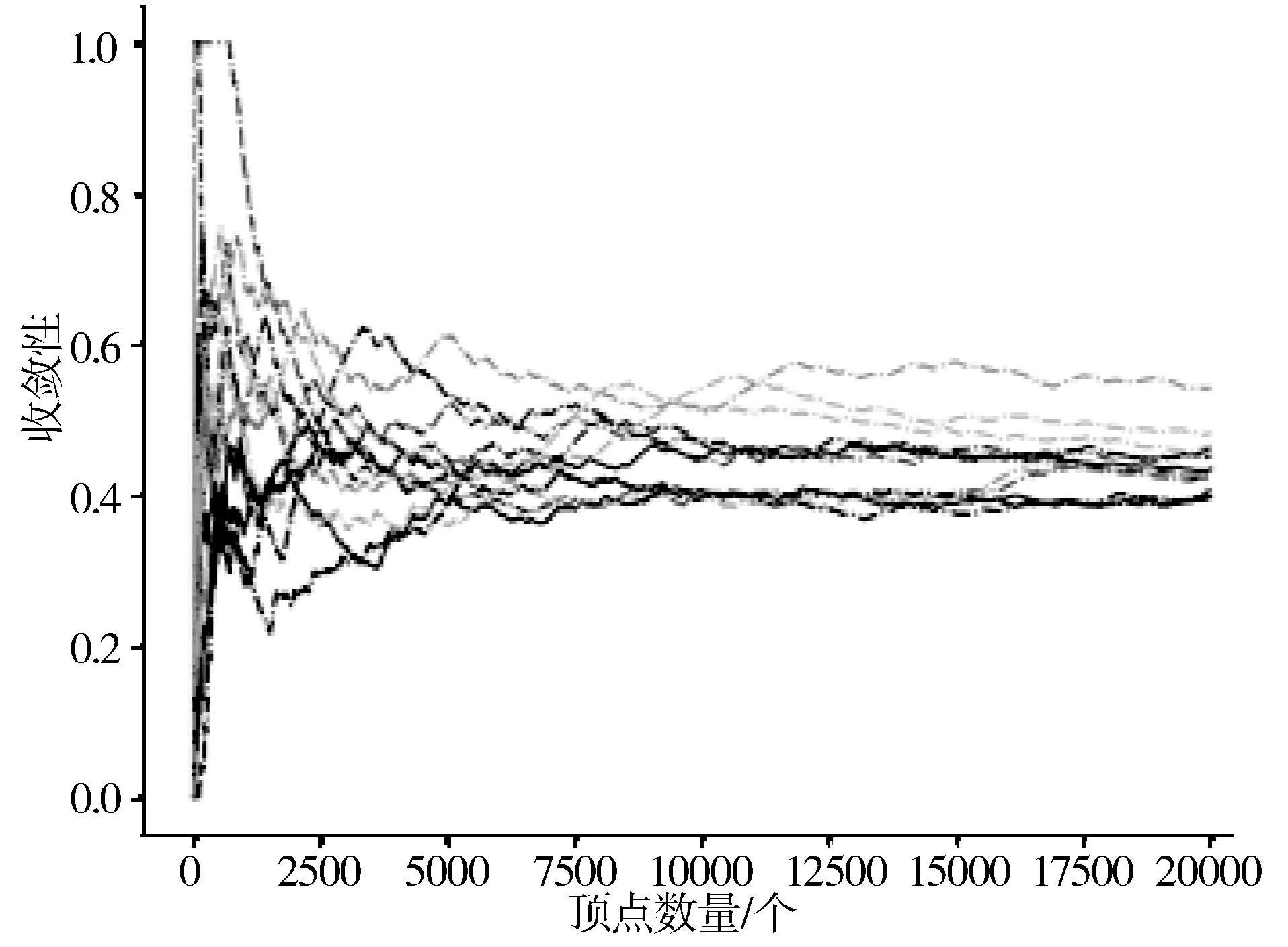
图7 UD采样方法的收敛性

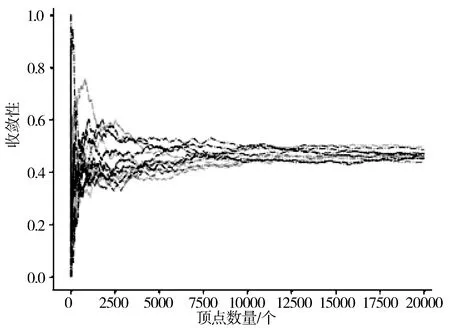
图8 AS采样方法的收敛性

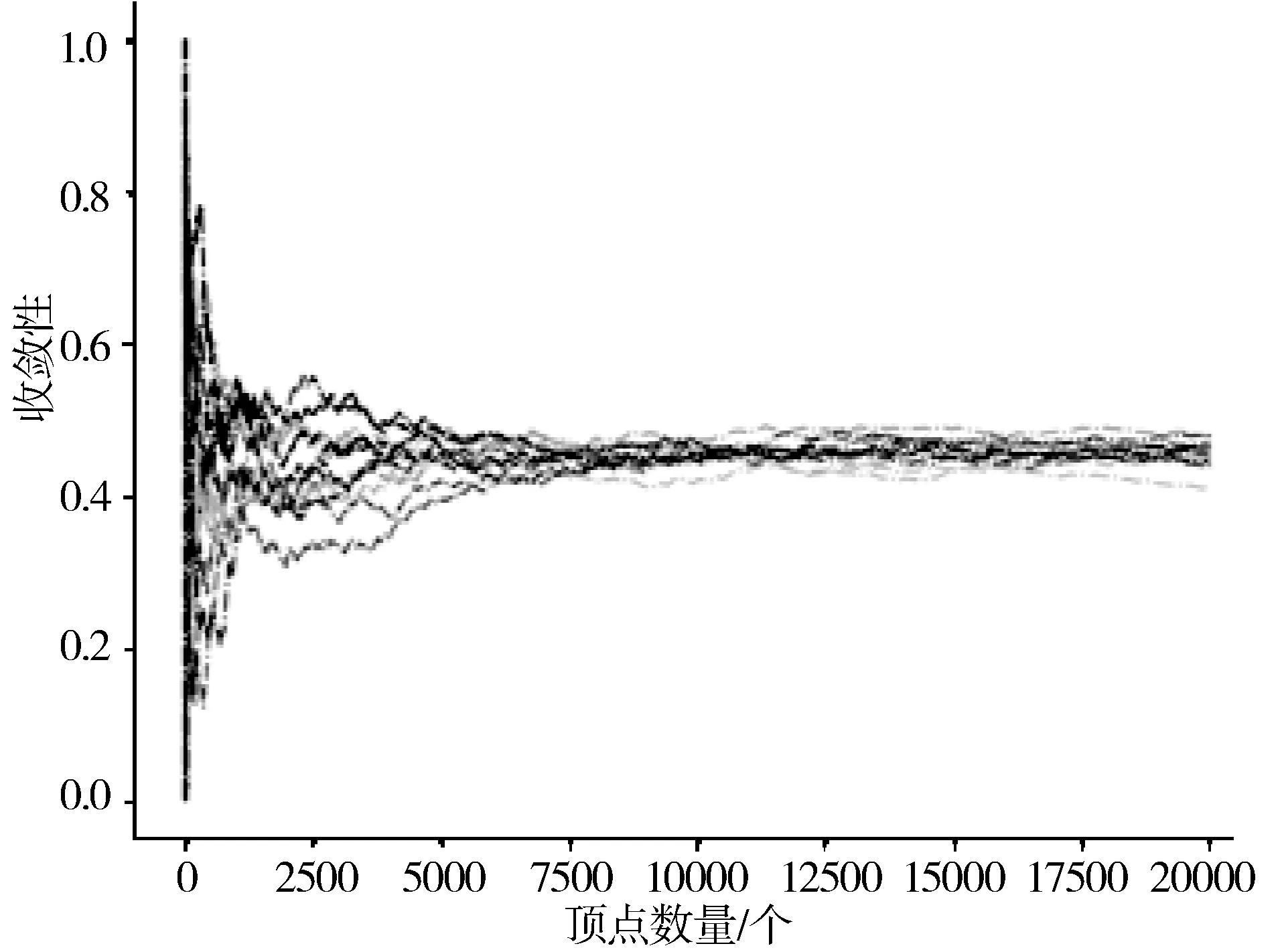
图9 JPS采样方法的收敛性

图6～图9中，横坐标表示采样的顶点数量，纵坐标表示收敛值，曲线的条数表示采样次数。可以看出，JPS方法的收敛性明显优于MHRW与UD采样方法，相较于AS方法也有部分改进。主要是由于在采样过程中引入了双重跳跃，因此确保了在采样过程中可以及时跳出连接良好的子区域和顶点的自循环。

结合以上对比实验可以看出，JPS采样方法的性能优于其他采样方法，是一种有效的社交图采样方法。

4 结束语

本文基于MHRW采样方法提出了改进的顶点采样算法JPS，它将双重跳跃机制、顶点缓存区以及多路并行应用到MHRW中。根据第3章的性能评估，JPS获取的样本网络度分布和样本顶点平均度更接近原始网络数据集，双重跳跃机制增强了检测整个网络的能力，适用于不同连接强度的社交网络，且有效地优化了MHRW中自循环率过高的问题，因此JPS是非常可靠的在线社交网络数据样本采集算法。在未来的工作中，将使用JPS采样方法测试更多的大型社交网络数据集，进一步改进JPS方法使其能够在线抽样真实的社交网络，以应对更多复杂情况。