基于广义全变分正则项的图像填补技术

陈颖频，柯素玲，黄慧滢，吴日盛，王灵芝

(闽南师范大学物理与信息工程学院电子工程系，福建 漳州 363000)

0 引 言

图像填补技术广泛应用于图像遮挡物体去除、古籍图像恢复等[1-2]。图像填补通常有2种方法，一种是通过偏微分方程的填补方法，另一种是通过全变分(Total Variation， TV)约束的方法填补图像[3-4]。基于TV约束的图像填补方法假定图像由分片常数组成，其一阶梯度具有稀疏先验特性，因此通过约束图像一阶梯度的稀疏性来实现图像修补工作[5-6]。与基于变分偏微分方程[7-8]的修复模型相比，TV修复方法具有更好的收敛性，在修复图像的同时，保持图像的边缘，并能有效压制噪声。值得指出的是，TV方法假定图像由分片常数组成[9-11]，在其修复结果中常常会出现阶梯效应。二阶广义全变分(Total Generalized Variation， TGV)正则项具有TV模型全部的优点，并考虑了图像的二阶梯度稀疏性，从而有效去除TV约束正则项导致的阶梯效应[12-19]。综上所述，本文引入二阶TGV正则项，提出一种新的图像修复模型，缓解TV模型在图像填补过程中产生的阶梯效应。然后采用一阶原始对偶算法[20-21]对提出的模型加以求解，该算法能有效地收敛并获得较好的恢复图像。在后续数值实验中可以看到，提出的方法能有效进行图像修复工作，同时又解决了TV图像修复模型的阶梯效应问题，并指出TGV在图像修复过程中存在的不足。

1 预备知识

1.1 全变分图像填补模型

一阶TV修复模型为：

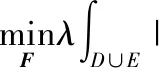
(1)

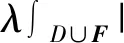
1.2 一阶原始对偶方法

本文引入一阶原始对偶算法求解提出模型，现在简要介绍该方法。假定求解问题的原始模型为：

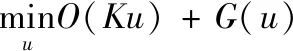
(2)

其中,K表示某种算子，如模糊算子、欠采样算子等；O和G表示2个不同的函数；u为式(2)的变量。

对式(2)引入共轭变换，转化为一阶原始对偶问题[20]，即：

(3)

其中，表示Ku和p的内积；p为对偶变量；O*(p)表示原始函数O对应的共轭变换函数。O*(p)定义如下：

O*(p)=sup{-O(u)}

(4)

其中，sup表示函数的上确界。

2 提出的图像填补模型与求解

2.1 二阶的广义全变分图像填补模型

二阶TGV正则项同时约束了图像的一阶梯度与二阶梯度，因此能有效缓解全变分模型的阶梯效应。基于二阶TGV正则项，本文提出一种新的广义全变分模型为：

(5)

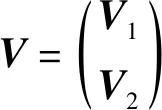
式(5)中的对称梯度算子定义如下：

其中，∂x+和∂y+分别表示横方向的前向差分和纵方向的前向差分。

2.2 提出模型的求解

对式(5)运用一阶原始对偶算法进行求解，引入对偶变量，则式(5)的一阶原始对偶形式为：

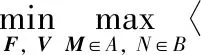
(7)

其中，M和F表示原始变量F和V的对偶变量；集合A和B表示M和F的可行域，定义如式(8)～式(9)：

A={M=(M1,M2),‖M‖∞≤λ1}

(8)

(9)

对于F变量，需要将填补区域和非填补区域分开求解。对于E区域，将式(7)中关于F变量在E区域的目标函数对F变量求导得：

(10)

利用半隐式梯度下降法得到E区域F变量的更新公式为：

=F(k)|E+τ[div(M(k))+β(G-F(k+1)|E)]

=F(k)|E+τ[div(M(k))+βG-βF(k+1)|E]

(11)

根据式(11)得E区域F变量的更新公式为：

(12)

对于D区域，将式(7)中关于F变量在D区域的目标函数对F变量求导，并利用梯度下降法，得F变量在D区域的更新公式为：

=F(k)|D-μ(-div(M(k))|D)

=F(k)|D+μdiv(M(k))|D

(13)

综合式(11)和式(13)可得F变量的更新公式为：

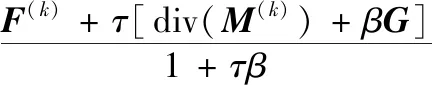
(F(k)+μdiv(M(k))|D

(14)

对于V变量，采取梯度下降法求解，得：

V(k+1)=V(k)+τ(M(k)+divh(F(k)))

(15)

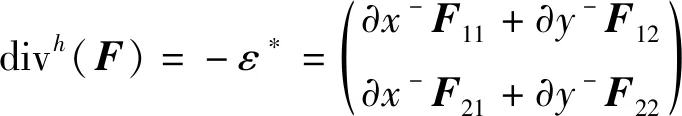
对于M变量，利用前向后向映射法求解，即：

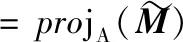
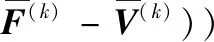
(16)

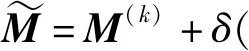
对于F变量，利用前向后向映射法求解，即：

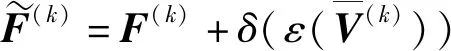
提出算法如算法1所示，算法1中的tol表示算法迭代停止阈值。

算法1基于TGV的图像填补算法。

Input:观测图像G

Output:修复图像F

Initialize:β,λ0,λ1,k=0,tol=10-4,T=1,F(k)=G,V(k),M(k),F(k)=0

1:WhileT>tol do

2:利用式(14)更新F(k+1);

3:利用式(15)更新V(k+1);

4:根据式(16)更新M(k+1);

5:根据式(17)更新F(k+1);

6:T=‖F(k+1)-F(k)‖2/‖F(k)‖2;

7:k=k+1;

8:End While

9:ReturnF(k)asF

3 实 验

本文使用6幅图像来做实验，用来验证提出算法的效果，如图1所示，图像的大小都是256×256。主要对比参数包括结构相似性(Structural Similarity， SSIM)[22]和峰值信噪比(Peak Signal to Noise Ratio， PSNR)。实验中的PSNR定义为式(18)，SSIM定义为式(19)。

(18)

其中，X表示原图，Y表示修复的图像，max(X)表示X中的最大像素值。

(19)

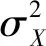
图1 测试图片

为了观察提出算法的图像填补效果，图2以Cameraman为处理图像，展示各种算法的图像恢复细节。对比图2(a)实线框框出区域，可以看到，图2(c)和图2(d)在该区域呈分片状，存在明显的阶梯效应，而本文方法的恢复图像(图2(e))在该区域的纹理细节恢复得更好，与原图更接近，这表明本文方法能有效缓解TV模型的阶梯效应，获得更好的视觉效果。

图2 基于Cameraman的算法对比图

实验中,将本文算法(简称为TGV)与TV方法、基于Lp伪范数的各向异性TV正则约束方法[23](简称为TpV)进行对比，对测试图片在不同损坏程度(损坏程度分别为10%、20%、30%，损坏程度表示像素点缺失的个数与图像像素个数的比例)前提下进行图像恢复，并将比较结果记录于表1。表1中，黑体加粗的指标表示比较算法中最高的指标，可以看到，本文方法获得最好的图像恢复指标。

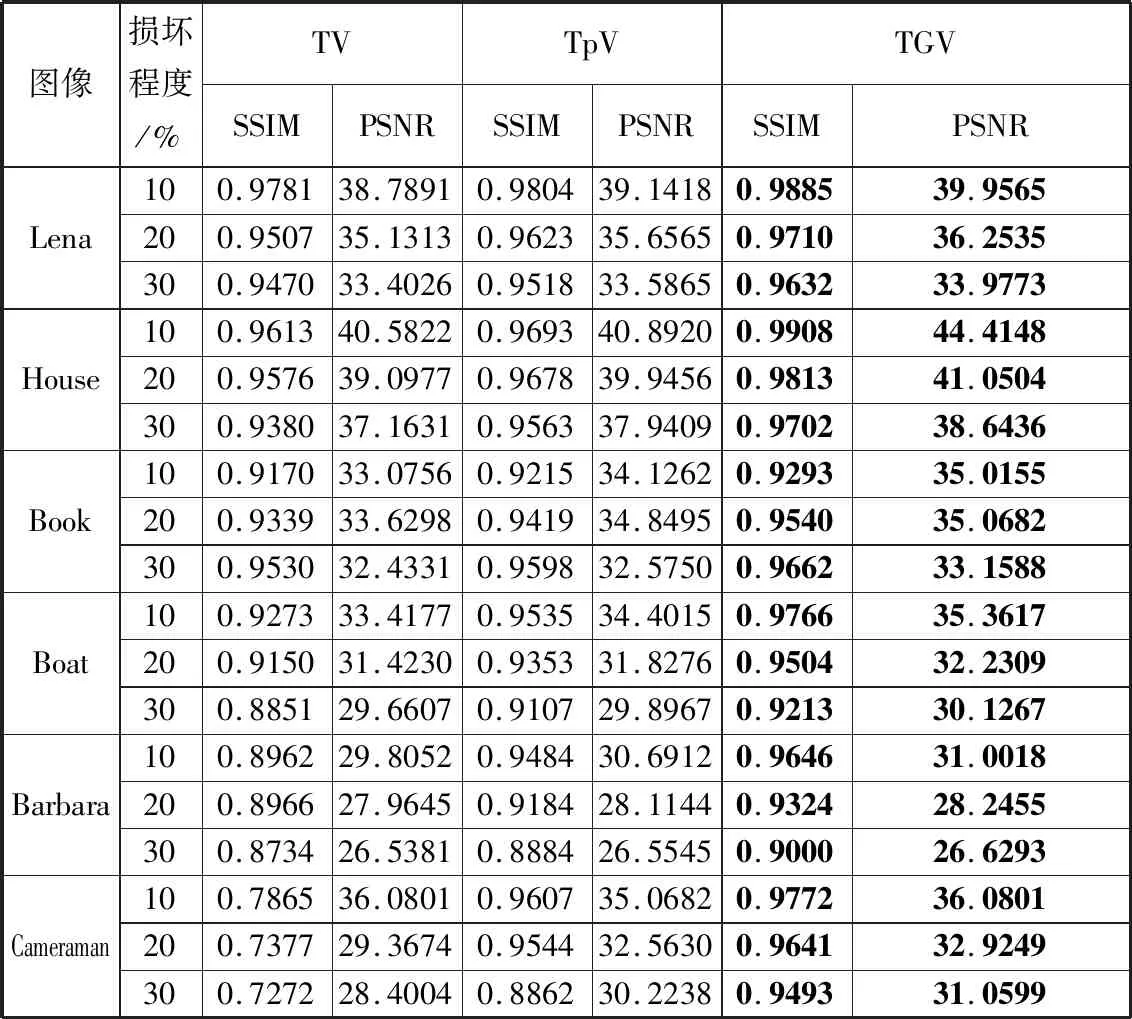
表1 算法性能对比表

值得指出的是，TGV方法也仅仅对局部损伤较少的图像有比较好的修复效果，当局部区域被大面积损坏的时候，TGV在这种区域上的填补效果并不佳。图3反映了TGV方法的这一缺点，本文在损坏图像的过程中，特意在Lena的帽子上增加了一块集中损坏的区域(详见图3(b)中由虚线框框出的区域)，这部分的图像恢复质量其实是不好的，可见基于TGV正则项的图像修补对于大范围损坏的区域的修复能力是有限的。相比而言，图3中实线框框出区域中，损坏区域不像虚线框框出区域中黑色块那么集中。从图3(e)可以观察到，TGV方法在实线框出区域的图像恢复质量就比虚线框出区域的恢复质量好得多。这说明，TGV方法需要依赖邻域信息来恢复损失的图像信息，如果邻域信息丢失得过多，那么TGV方法就无法有效恢复这个区域的图像。

图3 基于Lena的算法对比图

4 结束语

本文提出一种基于TGV正则约束的图像填补方法，充分挖掘图像二阶梯度的稀疏性，从而弥补了TV图像填补模型仅考虑图像一阶梯度稀疏性的局限。从实施的实验中可以得出如下认识：

1)实验结果表明，利用一阶原始对偶方法能有效求解基于TGV的图像填补问题，且基于一阶原始对偶的TGV填补方法相比于TV和TpV方法在视觉和客观评价指标方面都获得较好的效果，有效缓解了TV图像修复带来的阶梯效应。

2)基于广义全变分的图像修复技术也只能对轻微损坏的图像区域进行有效修复，然而，对于大规模的损坏区域，TGV方法也无法有效获得良好的图像修复效果。在未来的研究中，笔者将针对这一问题开展深入的讨论。