基于马尔科夫随机场的三维激光雷达道路场景分割

邹 斌，冯昊文,刘 康

(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室,湖北 武汉 430070;2.武汉理工大学 汽车零部件技术湖北省协同创新中心,湖北 武汉 430070)

地面自主智能车辆对环境感知是实现其功能的重要一环，智能车辆的传感器系统通常由激光雷达和相机等传感器组成，用来识别障碍物区域和地面区域。多线激光雷达采集车辆外部数据的能力非常强，每秒能输出上百万的测量点。怎样在这些数据中准确得到所需的目标区域是研究者们研究的重点[1-2]。

在使用三维激光雷达点云数据来分离路面点和非路面点上，三维激光雷达的数据结构特点是任意三维点与其在同一扫描线上相邻角度的点和前后扫描线相同的点组成4邻域系统，可以将三维点云以无向图的方式组织起来。根据激光点云环之间的距离来判断单个三维点是否属于地面区域[3]。Moosmann等[4]提出一种处理大量三维激光雷达测量数据的快速方法，通过使用局部凹凸性来分割地面和物体。Douilard等[5]采用Mesh方式构造图，并且通过梯度来确定地面点。朱株等[6]将扫描线x-y平面上的投影线进行分段，构造以线段为节点的马尔科夫随机场，求解随机场分离地面和障碍物。基于区域空间[7-8]的聚类法是使用较多、效果较好的区域分割技术，但初始化时的参数对其影响很大，有些情况必须人为干涉才能获得较好的结果。此外还有一种比较简单的阈值法[9]；该方法作为传统的道路场景分割的方法之一，在单一场景中的效果比较理想并且实时性较好，阈值的作用是区分不同区域的灰度并将不同的区域分成两类，该方法分离效果的好坏依赖于阈值的选取。

从三维激光雷达中获得原始点云数据，通过对点云数据建立栅格地图，计算所有栅格的梯度，然后根据栅格地图建立马尔科夫随机场，最后通过图割的方法对马尔科夫无向图模型进行求解，实现路面点云分割。利用马尔科夫随机场中只有相邻节点之间才存在关系的特性，较好地克服了坡道、多类型地面等问题，试验证明该算法有较好的效果。

1 算法概述

1.1 建立扇形栅格地图

笔者建立了一个2.5D的扇形栅格地图。由于车体的阻挡，极坐标内存在一定的盲区。文中取雷达扫描半径为42.3 m以内的点云，实测雷达的扫描盲区半径为1.3 m。扫描范围为-180°～180°。即建立一个外径42.3 m，内径为1.3 m的角度范围为-180°～180°的环形区域。所建立的栅格在环向上的分辨率为1°，径向上的分辨率为0.2 m。如图1所示，建立一个分辨率为180×200的栅格地图。然后依次计算每个栅格内点的平均高度Hmean、高度的最大差值Hdif以及最大高度Hmax，如果栅格内不存在数据点，只存储环向角度和径向长度。由于只获取车辆正前方的数据信息并做实时处理，车辆后方的数据作为非目标点，并且将车辆正向X轴大于0，Z轴方向小于车身高度的点作为目标点来建立栅格地图。

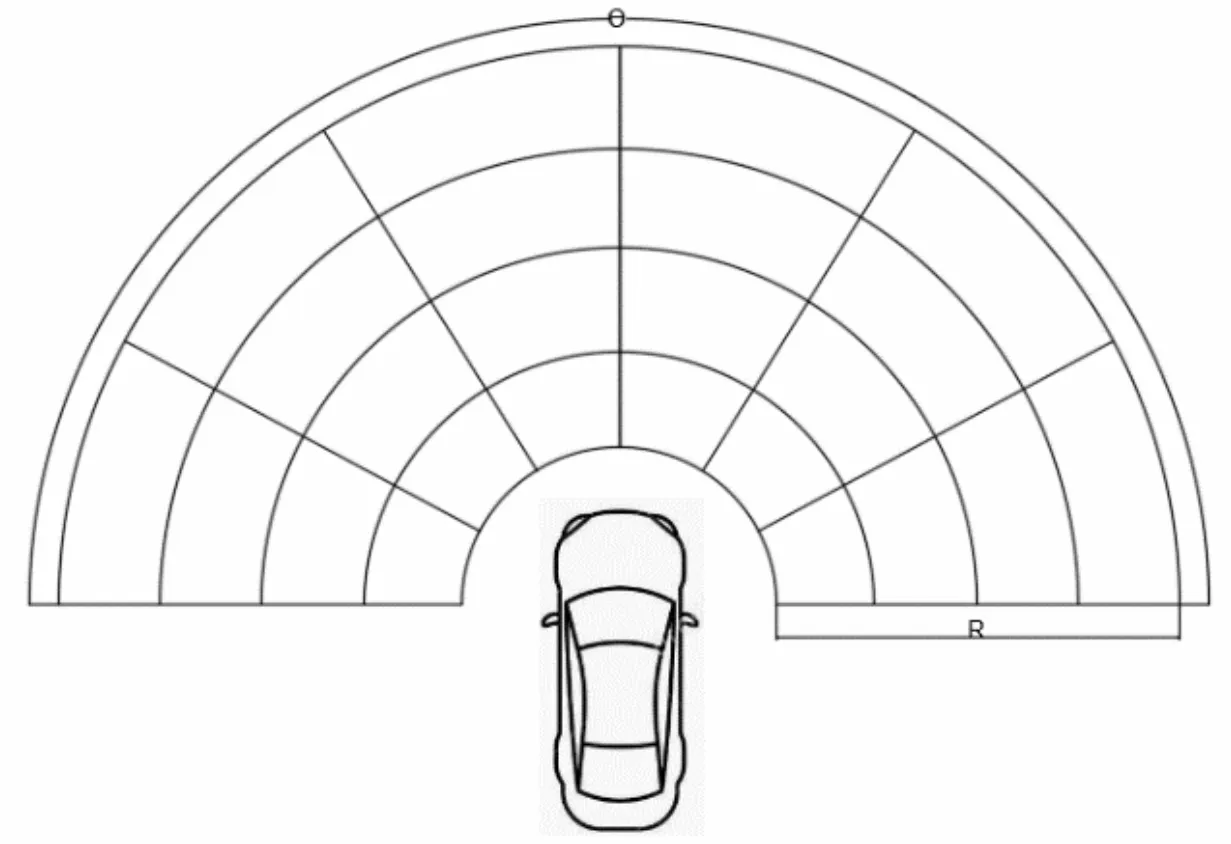
图1 车辆前方栅格示意图

1.2 栅格梯度值的计算

环向上栅格之间的距离Dci的计算公式为：

Dci=Δi×j

(1)

径向上栅格之间的距离Dri的计算公式为：

Dri=Δj

(2)

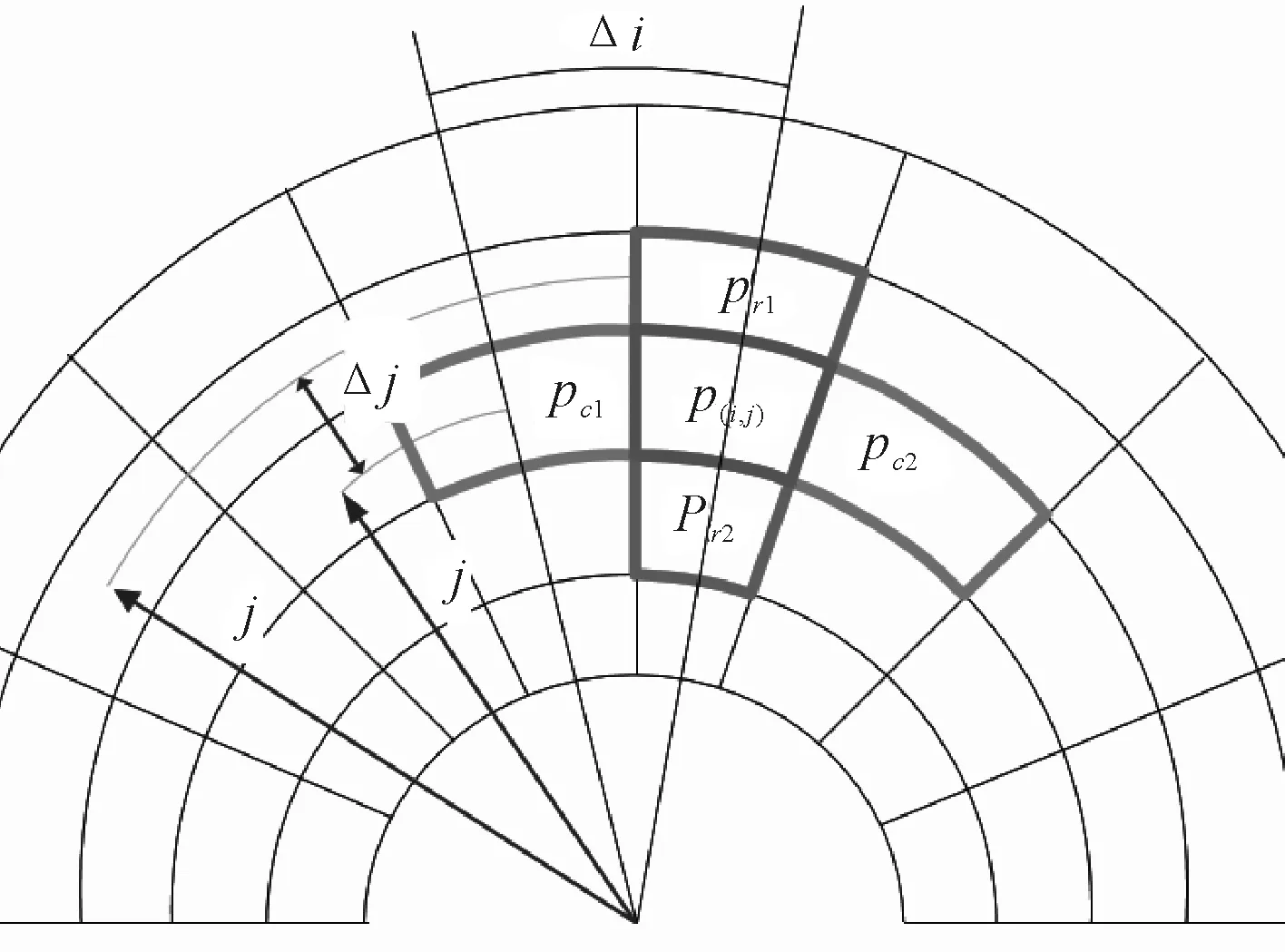
图2 相邻点选取

式中：Δi为环向上pci与p(i,j)的角度差；r为同一环形栅格的半径；Δj为径向上相邻栅格的半径差。

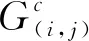
(3)

(4)

由于计算梯度反映的是垂直位移相对于道路几何中水平距离变化的变化，因此梯度较大的节点是沿着不同障碍物的边界，这是比垂直位移本身更敏感的道路分类标志。图3为建立的梯度栅格地图，图中深灰色表示梯度接近0，亮白色表示的梯度值较高。

图3 梯度栅格地图

1.3 马尔科夫随机场的建立与求解

栅格地图可以表示为具有180×200个元素组成的位置集合S={1,2,…,n}，标号集合表示为L={Bground，BN-ground}，在标号集合L中为位置集合S中的每个元素分配一个标签，这就形成了S到L的映射。

随机场为R={Ls,s∈S},如果随机场R满足式(5)的性质，式(5)中N(s)⊂S，s∉N(s)，∀s,r∈S,s∈N(r)⟺r∈N(s),N(s)为s的领域集。

P(L(s)=l(s)|L(r)=x(r),r≠s∀r∈N(s))=

P(L(s)=l(s)，L(r)=x(r), ∀r∈N(s))

(5)

马尔科夫随机场建立完成后，为随机场中每个位置赋予标签L，建立所分配标签正确度的能量优化函数，通过不断优化能量函数来优化标签分配的正确度，即为马尔科夫随机场的求解。图4由节点和节点与节点连接的边来组成的，节点表示为v，其集合表示为V；边表示为e，其集合表示为E。随机变量A，B，E满足:

P(A,E|B)=P(A|B)P(E|B)

(6)

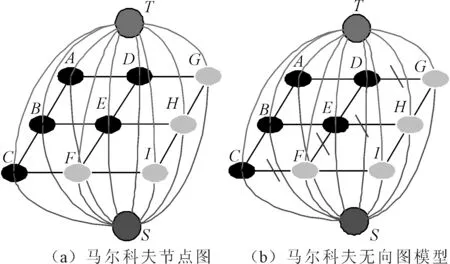
图4 马尔科夫随机场示意图

定义源点T、S，源点与各个节点之间边也赋予一定的权重D(vi)表示。该值量化各个节点和T、S的相似程度。定义能量函数为：

(7)

式中：D(f(vi))为数据项，W(f(vi),f(vj))为平滑项。

首先根据梯度值为边集赋予权值，在赋权值之前，赋值函数f(vi)为每个节点的梯度值分段赋值，然后根据每个栅格的梯度等级为每个栅格节点赋予标签，该节点被赋予标签后的代价函数为D(f(vi))，f的定义如下：

(8)

采用类似阶跃函数将各个栅格的梯度分等级赋值。μ为阶跃函数参数，其大小根据具体梯度值选择。文中μ=102，tn=10，G(i,j)为栅格节点V(i,j)的梯度。D(vi)赋权值，赋值函数定义如下：

D(f(vi))=λmin(||G(i,j)|-f(vi)|×Δ，τ)

(9)

式中：λ为比例因子，取0.5；τ为常数，取25。

比例因子λ控制数据项和平滑项的相对权重。常数τ可以使赋给各个节点的权值保持在一定的范围内，可以避免由于权值过大对运算带来的不利影响。定义W(f(vi)，f(vj))赋值函数如下：

W(f(vi),f(vj))=min(|f(vi)-f(vj)|,ρ)

(10)

式中:ρ为常数，取30。同理常数ρ可以避免梯度差异过大。

这样路面点与非路面点分割简化为寻找割集Uc，割集代价和用|Uc|表示，如式(11)所示。

(11)

在早期获得最小割的方法是设置一个固定阈值，割集Uc为权值小于阈值的边，但此方法只适用于简单场景。Jr等[10]提出了最大流方法，文献中证明了最大流即为最小割。求取最小割的方法有很多，其中Boykov[11]等人的最大流算法较为优秀。

2 试验结果与分析

笔者使用的智能车试验平台如图5所示，Velodyne 16线三维激光雷达安装在车辆顶部，同时车内安装了高配置的运算平台硬件，为了能协调多信息采集任务，保证运算的实时性，本文算法是在Ubuntu下的ROS机器人实时操作系统下运行的。所采集的校园路况数据如图6所示，粗线表示车辆行驶采集信息的路线。

图5 智能车试验平台

图6 采集路线

将本文算法在智能汽车试验平台上进行实车测试，路况为校园路况并进行了坡道测试，图7(a)为试验目标的坡道，为校园内的一段坡道；图7(b)为基于马尔科夫随机场的路面分离结果；图7(c)为高度阈值算法在坡道测试的结果。从图7中可以看出高度阈值算法随着路面的坡度的加大，分离结果较为不理想，由于高度阈值的选取是固定值，通过单一的高度信息来分离路面效果不佳，存在大量的误判，图7(c)中椭圆形区域为误判，导致前方坡道为非可行驶区域。图7(b)为基于马尔科夫随机场算法检测结果，由于前方坡道在梯度变化方面变化不大，因此前方不存在误检区，可以看出本文提出的算法鲁棒性较强。

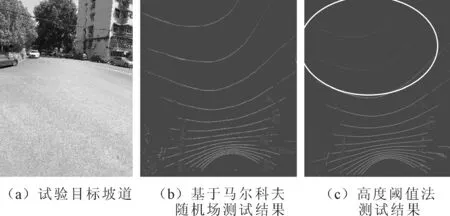
图7 试验结果对比

文中使用了kitti数据集中的城市公路测试，kitti数据集中进行的是实车测试，试验平台中使用的是Velodyne 64线激光雷达，数据中的车辆在城市公路工况下车速较快，车辆上下振动较大，这就需要算法具有较强的鲁棒性。本文算法与高度阈值算法进行了对比。图8(a)为直线缓坡的结构化城市道路，可以看出前方是有一定角度的坡道，图8(b)为高速路况下本文算法的路面分离结果，图8(c)为高度阈值算法的分离结果。图9(a)为弯道的结构化城市道路，图9(b)为本文算法的分离结果,图9(c)为高度阈值算法的分离结果。由于弯道内侧较低，弯道外侧较高，采用的综合计算轴向梯度和环向梯度的方法，避免了单方向过大或者过小对梯度计算的影响，因此在弯道中有较好的效果。

图9 城市工况弯道试验对比

另外在测试中发现64线激光雷达由于线束较为密集，路面相邻的栅格点梯度差别较小。16线激光雷达线束较为稀疏，尤其在远处，线束间可以相差3米以上，导致梯度变化很小，因此对16线激光雷达算法上进行了弥补：

(12)

式中：θ为线束纵向角与水平线的夹角；∂为增益系数，根据试验确定。

为了测试算法的稳定性，采集kitti数据集中激光雷达在高速公路上采集100帧数据，并对每帧中的所有栅格进行人工标记，与文中算法结果进行对比。正确率R=Nm/Nt，Nm为文中算法属于地面的栅格数目，Nt为人工标记的地面栅格数目，试验结果为92.45%。

3 结论

笔者利用栅格地图的梯度建立马尔科夫随机场来分割路面点与非路面点，利用最大流的方法对马尔科夫随机场进行求解。在不同工况下都进行了试验并与高度阈值法进行对比，从结果来看在缓坡和弯道的地面类型上，有良好的分离结果。不同线束的激光雷达，线数越密集，马尔科夫随机场节点之间的相邻信息越丰富，同时本文采取的算法在鲁棒性方面要明显优于高度阈值法。