基于Simulink/Trucksim的四轴分布式电驱动车辆的建模与仿真

李佳欣，杨 波，裴晓飞

(1.武汉理工大学 汽车工程学院，湖北 武汉 430070; 2.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070)

纯电动汽车按驱动系统结构可分为两大类：集中驱动式和分布驱动式。以电动轮为代表的分布式驱动形式具有更多的优势使分布式电驱动车辆逐渐成为新能源汽车行业的研究热点[1-2]。

在进行分布式电驱动车辆的动力学控制的相关研究时，文献[3]基于非线性七自由度车辆模型研究汽车的状态参数预测与操纵稳定性控制；文献[4]搭建了四驱电动汽车的10自由度模型，该模型考虑了车辆的纵向、横向、侧向、俯仰、侧倾、簧载质量的垂向运动以及4个车轮的转动自由度。该文献的模型考虑了包括悬架在内的运动，模型精度较高。除此之外，东京大学、美国俄亥俄州立大学的学者们为了研究四轮独立轮毂驱动车辆的动力性而搭建了动力学模型[5-6]。但以上文献均为四轮分布式电驱动车辆的稳定性控制的相关研究，四轴分布式汽车的动力学模型更为复杂，因此在研究车辆的横摆稳定性时，不能够直接采用相同的控制策略。

为了更好地研究四轴车辆的操纵稳定性，基于Matlab/Simulink建立四轴分布式电驱动车辆的动力学模型，通过参数化建模方法使得该模型的通用性更高，并通过与Trucksim联合仿真的方式，进行车辆动力学模型的验证，确定该模型的准确性和可靠性，为后续的稳定性研究与控制打下基础。

1 车辆动力学模型搭建

目前常用于汽车建模与仿真的软件主要有MATLAB/Simulink、AMEsim、ADAMS、SIMPACK、Carsim、Trucksim等[7]。而MATLAB/Simulink是以图形化和参数化的建模方法来搭建汽车模型的软件，故在整个过程中，用户可以建立一个系统分类更为清晰明确的模型，并且由于采用参数化建模的方法，使得用户能够较为直接和简单的根据相关需求修改系统的参数或者动力学方程[4]。故在本文中采用MATLAB/Simulink软件建立参数化的汽车动力学模型。

1.1 坐标系与自由度

由于多轴分布式电驱动车辆的数学模型较为复杂，为了针对性地研究车辆的横摆稳定性，笔者将主要考虑与车辆横摆稳定性相关的运动，故在搭建该模型时将重点放在与平面运动和横摆稳定性控制相关的自由度，故忽略车辆的俯仰、侧倾以及车轮跳动的自由度。因此该模型包括车身的纵向、侧向、横摆这3个自由度，每个车轮的转动总共8个自由度，再加上转向1个自由度，总共12个自由度。

汽车坐标系如图1所示，X-O-Y为大地坐标系，x-o-y为车辆行走坐标系。r为车辆的横摆角速度，β为车辆质心侧偏角，u、v分别为车辆在x-o-y坐标系上的纵向车速和横向车速。

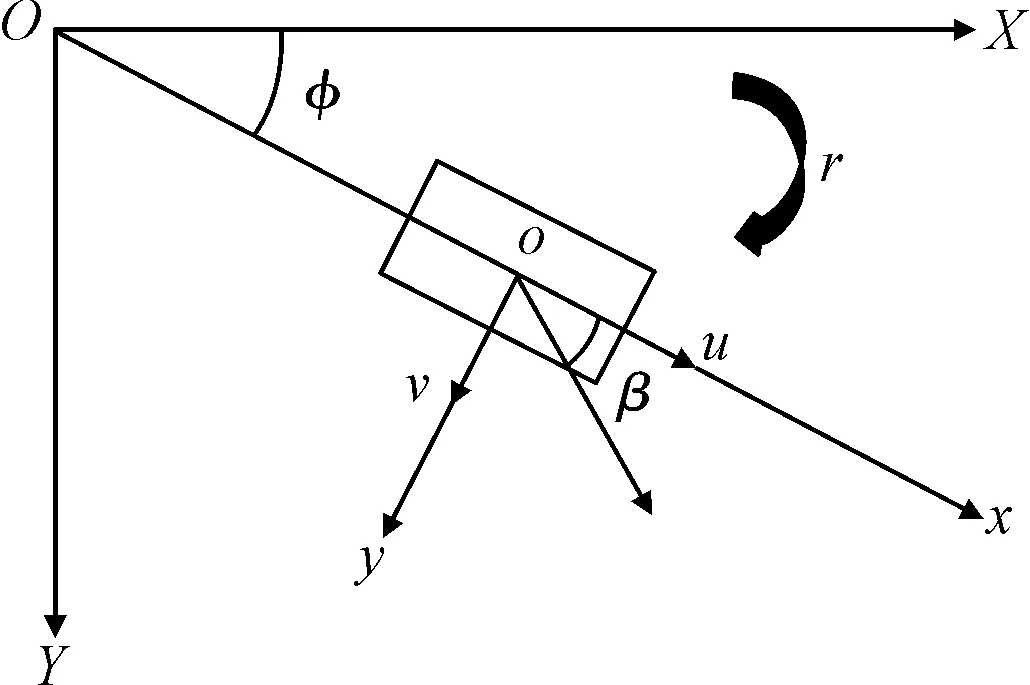
图1 坐标系示意图

1.2 车体模型

如图2所示为车辆整体模型。其中，车辆的轮距为B，轴距为L，质心高度为h。L1、L2、L3、L4分别为第一轴至第二轴、第二轴至质心、质心至第三轴、第三轴至第四轴的水平距离。当汽车在运动时，车轮受到各轮毂电机施加的驱动力矩Ti，地面施加给车轮的制动力矩Tbi，以及滚动阻力矩Tfi。沿车辆行走坐标系方向，路面通过各轮胎作用在整车上的各车轮受到的车轮纵向力为Fxi，侧向力为Fyi，横摆力矩为Izz。

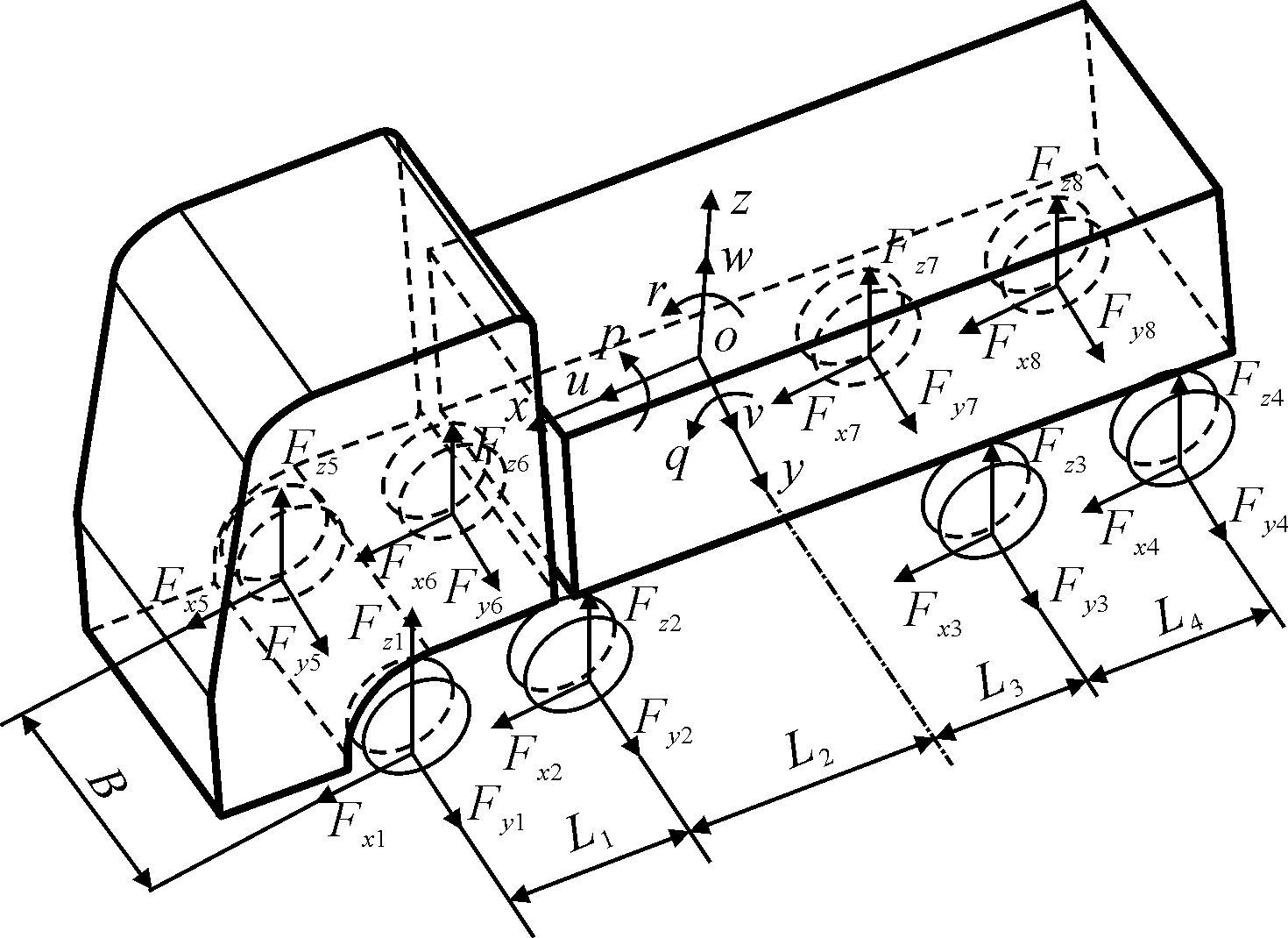
图2 车辆整体模型

由于本文的模型忽略了汽车俯仰运动和侧倾运动，故根据动力学平衡方程可以得出多轴分布式电驱动车辆在纵向、侧向以及横摆运动的运动平衡方程如下[8]：

(1)

(2)

L2(Fy3+Fy4)-L3(Fy5+Fy6)-(L3+L4)(Fy7+Fy8)+

(3)

式中:Fxi与Fyi为各个车轮在大地坐标系下的纵向分力与侧向分力;m为整车质量；g为重力加速度；f为摩擦力；α为坡度角；Cd为空气阻力系数；A为车辆迎风面积；I为力矩；u为纵向速度；v为侧向速度。纵向分力、侧向分力与车轮在车辆运动坐标系下的轮胎力的关系如下：

Fxi=Fxwicosδi-Fywisinδi

(4)

Fyi=Fxwisinδi+Fywicosδi

(5)

式中:Fxwi与Fywi分别为车轮沿轮胎方向的纵向轮胎力与侧向轮胎力；δi为各个车轮的转角。

1.3 悬架模型

由于在建模时忽略车辆的俯仰运动和侧倾运动，故在考虑垂向载荷转移的问题时，只考虑由纵向加速度和侧向加速度引起的惯性力所导致的载荷转移。因此各个轮胎受到的动态垂向载荷为静态垂向载荷与纵向加速度和侧向加速度产生的惯性力的矢量和[9]，受力关系如图3所示。

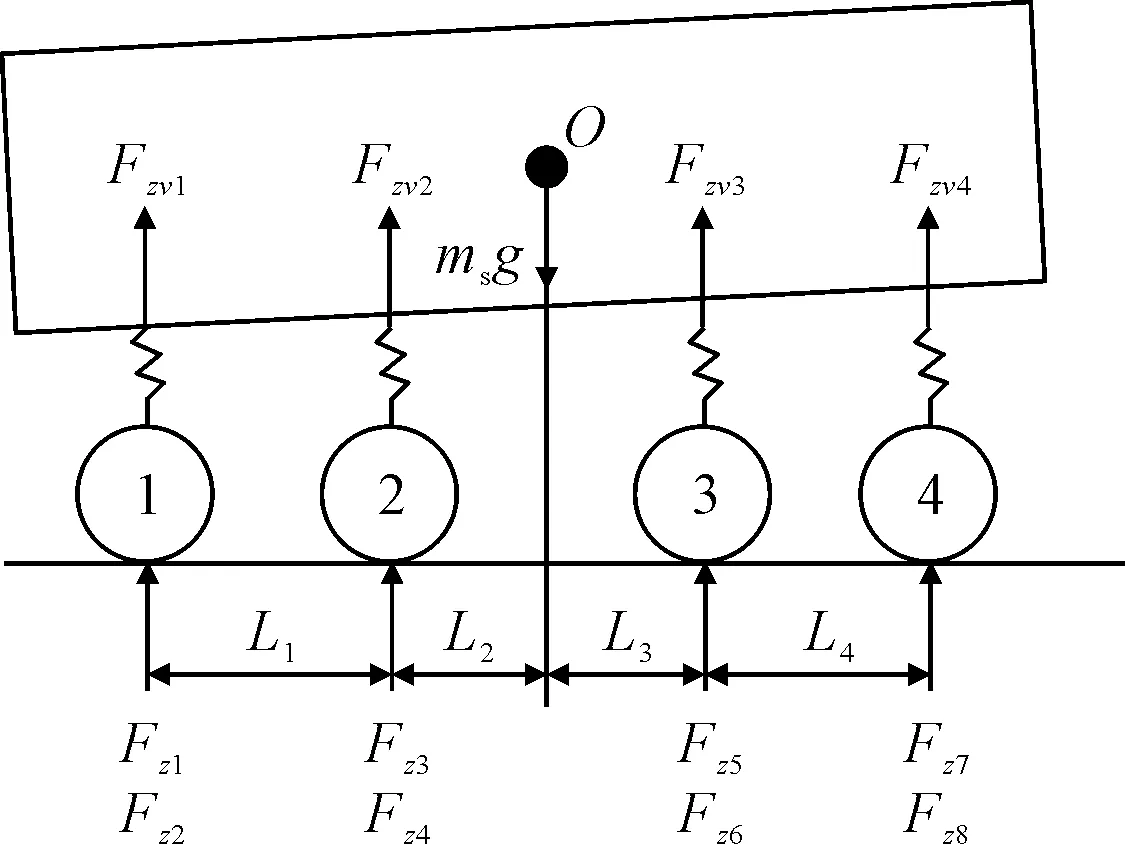
图3 车辆静态平衡受力图

各轴所受的静态悬架力Fzvi为：

Fzvi=

(6)

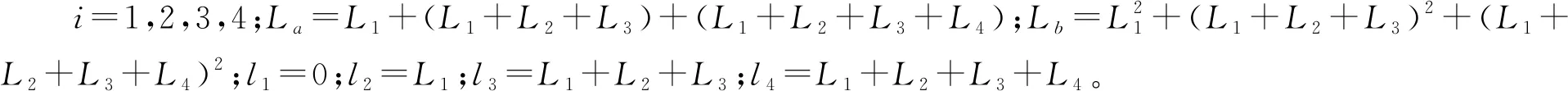
左右各车轮的静态垂直载荷Fzwi为：

(7)

式中：ms为簧上质量。

因此可得到各个车轮的动态垂向载荷的计算公式如下：

式中：ki与ei分别为根据力与力矩平衡方程求得的系数；ax、ay分别为纵向加速度和侧向加速度。

1.4 车轮运动模型

根据建模要求，考虑车轮在平面内的旋转自由度，并根据此自由度的受力情况建立车轮的运动模型如图4所示。

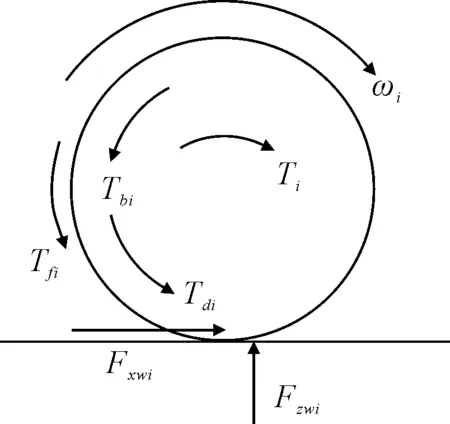
图4 车轮受力模型

从图4可知，在车轮旋转运动的方向上，电动轮受到的驱动力矩Ti、制动力矩Tbi、反力矩Tdi以及滚动阻力矩Tfi的动力学平衡关系为：

(9)

式中:ig为传动比;Iw为车轮转动惯量;ωi为车轮旋转角速度。

1.5 轮胎侧偏角和滑移率方程

忽略侧倾和俯仰运动对速度产生的影响，各轮轮心速度可由整车质心速度和横摆角速度表示，因此得到各车轮轮心速度沿车辆坐标系x轴的速度分量为：

(10)

沿车辆坐标系x轴的轮心速度和y轴的轮心速度分别为：

(11)

vyi=v±di·r

(12)

因此得到各个轮胎的侧偏角αi与滑移率λi如下：

(13)

(14)

式中：di为各轴轴距；rw为车轮半径。

1.6 转向模型

根据阿克曼转向模型建立如图5所示的模型，通常多周转向的所有车轮都具有同一个瞬时转向中心。为简化转向模型，假定车辆转向系统的传动比不变为iω，传动比设定为转向盘转角与第一轴左侧车轮转角之间的比值，同时设方向盘转角为δω。则根据图5中各个车轮转角的几何关系可得：

(15)

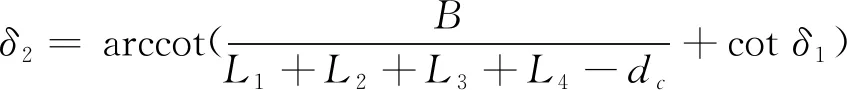
(16)

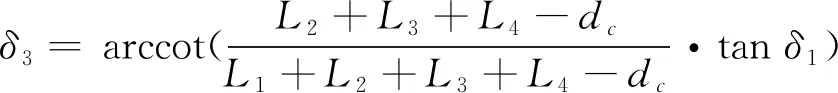
(17)

(18)

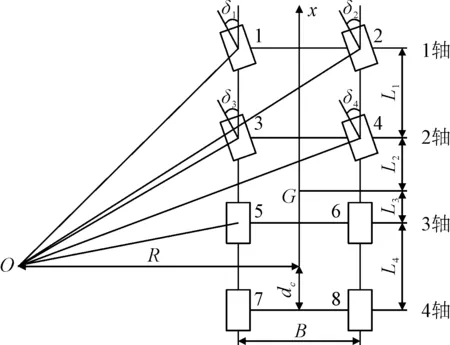
图5 转向模型

2 车辆动力学模型的实现

2.1 整车动力学模型

图6为通过Matlab/Simulink实现的整车集成模型，驾驶员输入方向盘信号给转向模块，转向模块通过Matlab Function函数表示出前两轴的4个转向轮的转角并输出给车辆运动模块。车辆运动模块的输入包括4轮转角和8轮转矩，输出为8轮转速和纵向速度、纵向加速度、侧向速度、侧向加速度和横摆角速度等，若在后续研究中需要其他参数，可在Simulink中增加相应的输出。转速转换模块是将车辆运动模块输出的车轮轮速转换为电机转速并输出给电机模块，以便电机模块计算出对应的各个车轮的驱动力矩。

2.2 车辆运动模块集成

车辆运动模块包含魔术轮胎公式、车辆动力学模块、车轮旋转模块和侧偏角与滑移率模块。魔术轮胎公式通过Matlab function模块编程实现，得到了车辆在不同工况下的8个轮胎的纵向力和侧向力，并给车辆动力学模块作为输入。侧偏角与滑移率模块通过S-function模块编程实现，通过该模块可得到各个车轮的侧偏角与滑移率，并作为轮胎魔术公式的输入。

车辆动力学模块包括车辆的纵向动力学方程、侧向动力学方程和横摆动力学方程，分别通过Simulink的模块化建模表示车辆的运动状态，得到各个轮胎的垂向力和各个自由度上的速度与加速度。图7为车辆的纵向动力学模型。

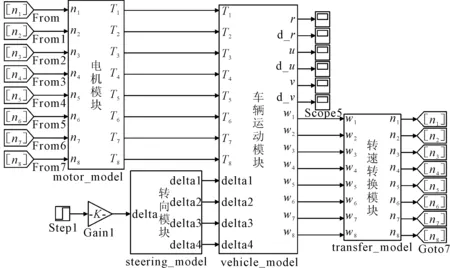
图6 整车集成模型

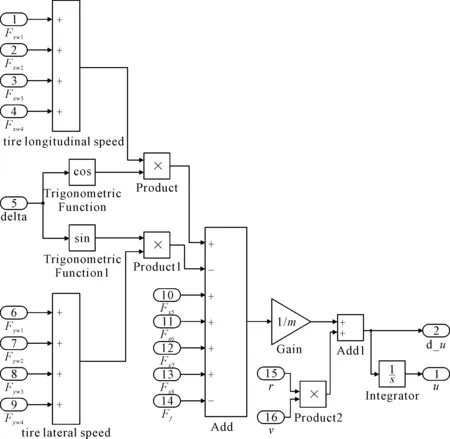
图7 车辆纵向动力学模型

2.3 车轮旋转运动模块

图8为车轮旋转运动模型，该模型是计算车轮地面作用力的子系统，通过该模型可以得到8个轮胎的实时转速，并将之输出给侧偏角与滑移率模块作为计算参数。

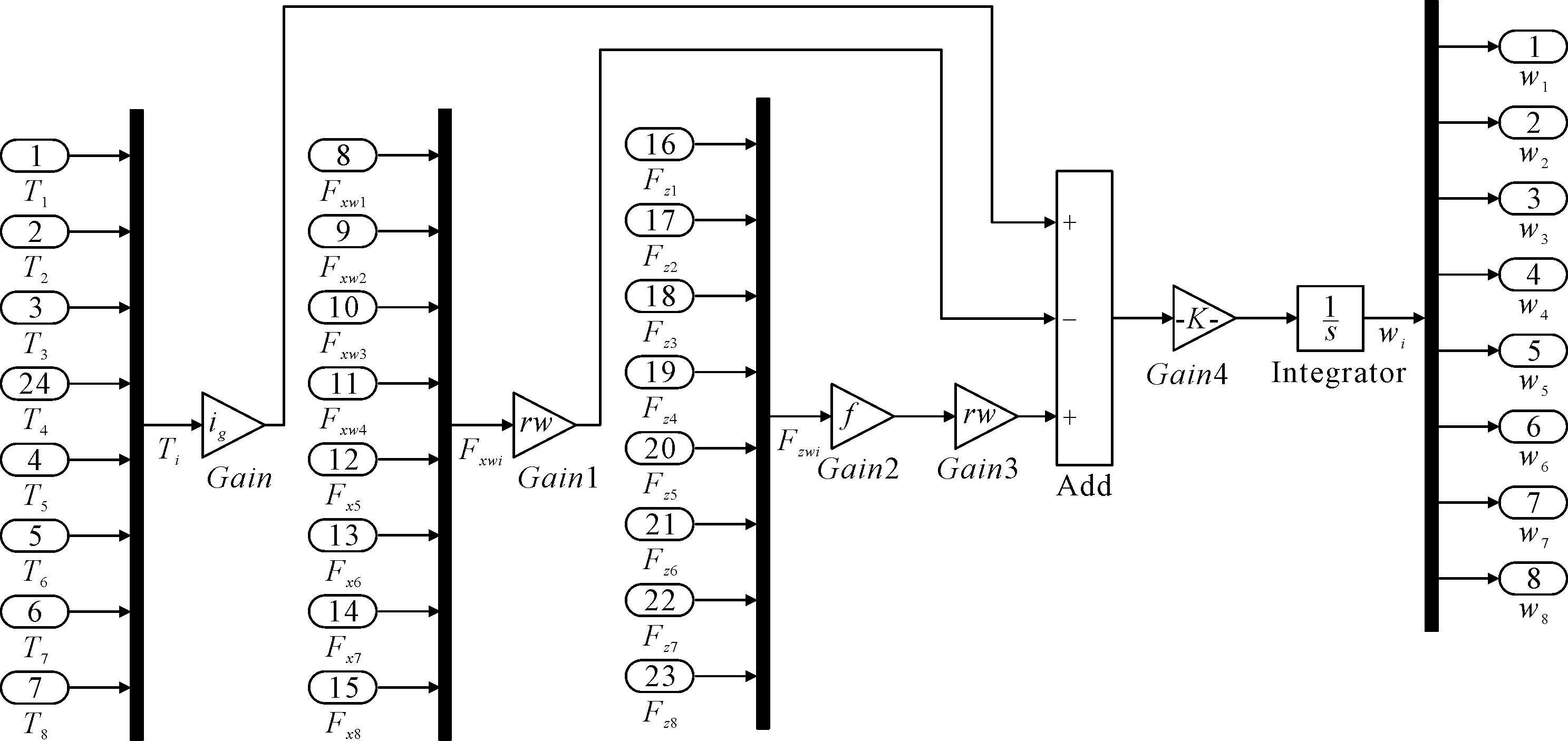
图8 车轮旋转运动模型

2.4 转向模块

转向模块根据转向模型公式，通过Matlab function和S-function实现了方向盘转角向车轮转角的转换。并将编程计算得出的4个转角分别作为后续多个模块的输入参数，转向模块如图9所示。

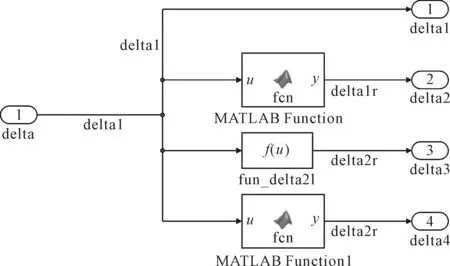
图9 转向模型

3 Simulink/Trucksim联合仿真

采用Simulink与Trucksim联合仿真的方式验证模型的精确性与可靠性[10]。根据后续研究车辆的参数，设置模型的基本参数为：整车质量为12 200 kg，质心高度1.2 m。第一轴到第二轴的水平距离为1.3 m，第二轴到质心的水平距离为0.5 m，质心到第三轴的水平距离为0.85 m，第三轴到第四轴的水平距离为1.35 m。左右轮距为1.863 m。车轮转动惯量为20，车辆绕z轴(垂直轴)的转动惯量为60 000 Kg·m2，轮胎半径0.6 m。设定车辆的初速度为70 km/h，车轮无制动。

3.1 方向盘转角阶跃输入

在Simulink与Trucksim中设置方向盘转角阶跃输入信号如图10所示，车辆仿真车速设置为80 km/h，摩擦系数μ=0.85；车速为30 km/h，摩擦系数μ=0.3。

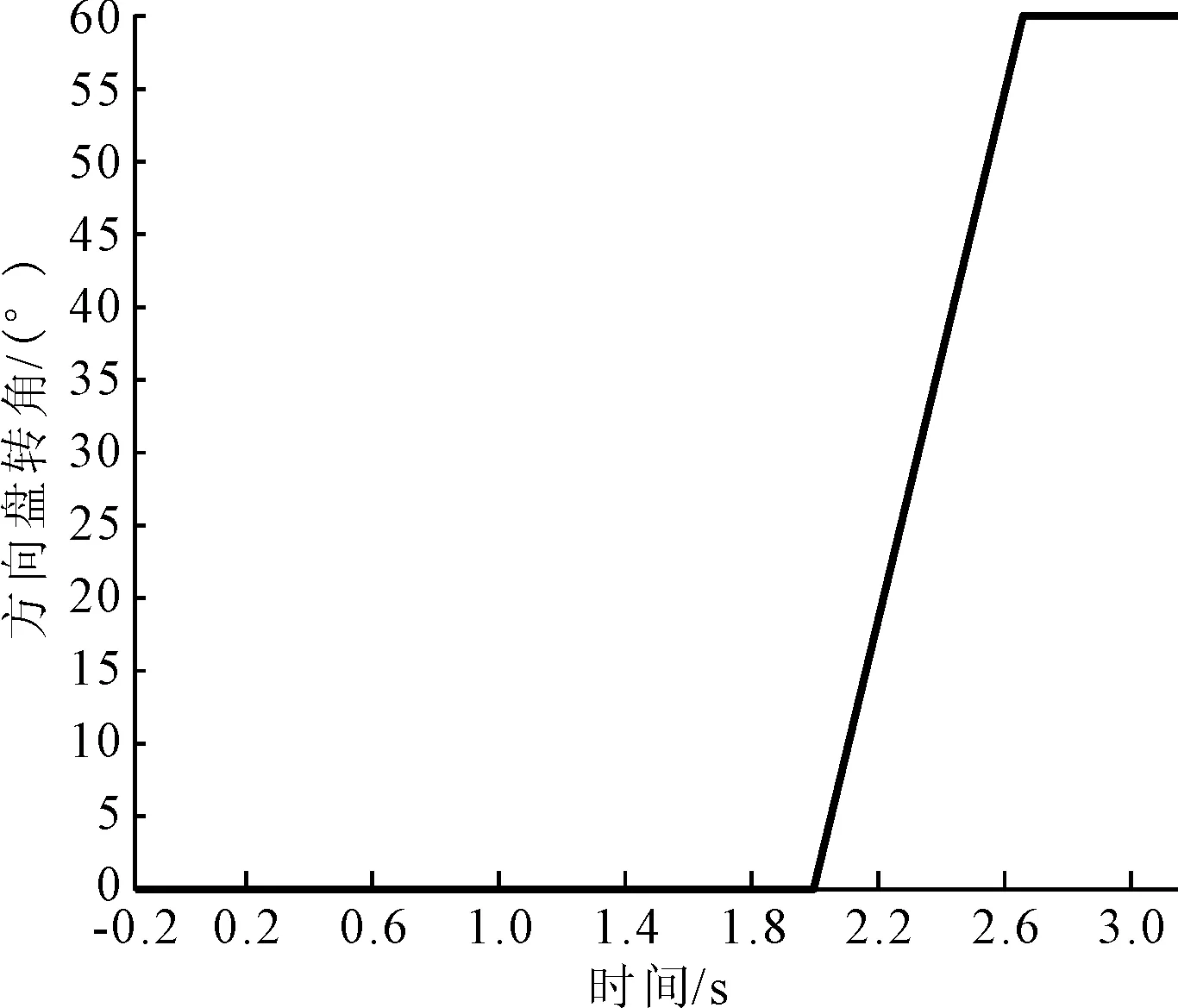
图10 方向盘转角阶跃输入信号

3.1.1 高附着路面仿真结果

在高附着路况下仿真后得到侧向加速度与横摆角速度的对比图如图11和图12所示。从图11和图12可知，在高附着路况下，仿真模型与Trucksim对比模型的侧向加速度走势和峰值基本一致，仿真模型的响应稍许有些滞后，但是并不影响模型的整体精度，并且最终稳定的侧向加速度也几乎相同。仿真模型的横摆角速度在接近峰值时有轻微波动，但误差在允许范围内，且变化趋势和峰值大小以及最终稳定后的值与对比模型基本相同。

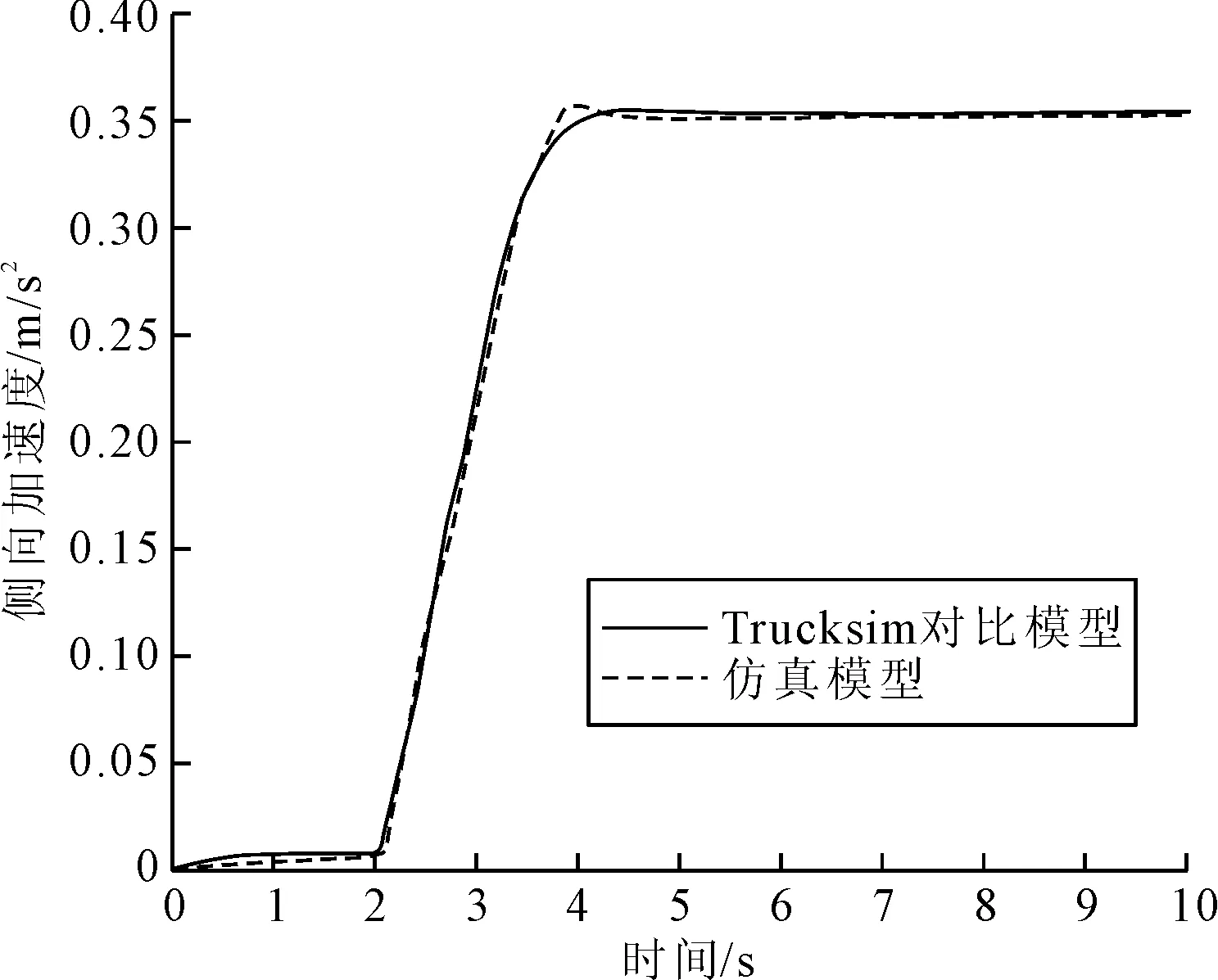
图11 高附着路面侧向加速度

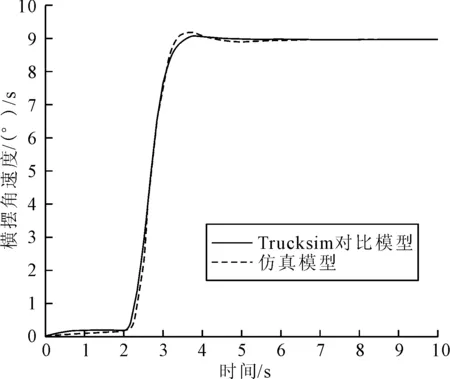
图12 高附着路面横摆角速度

3.1.2 低附着路面仿真结果

在低附着路况下仿真后得到侧向加速度与横摆角速度的对比图如图13～图14所示。从图13和图14可知，仿真模型的稳定性与Trucksim对比模型一致，侧向加速度的反映略有滞后，但是在可允许的范围内，且最终稳定值与对比模型一致。通过以上分析可得出仿真模型在方向盘转角阶跃输入的工况下具有可靠性和准确性。

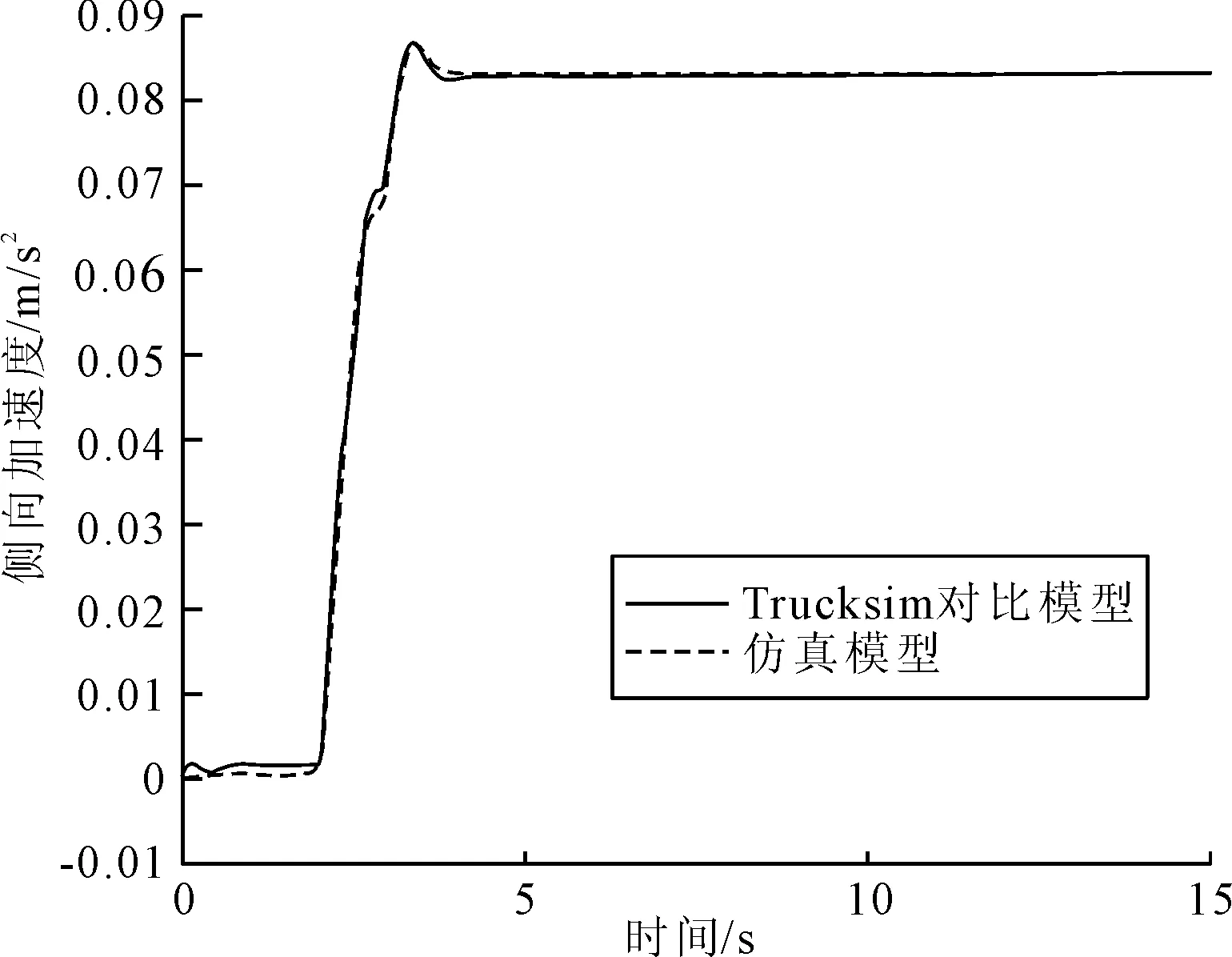
图13 低附着路面侧向加速度

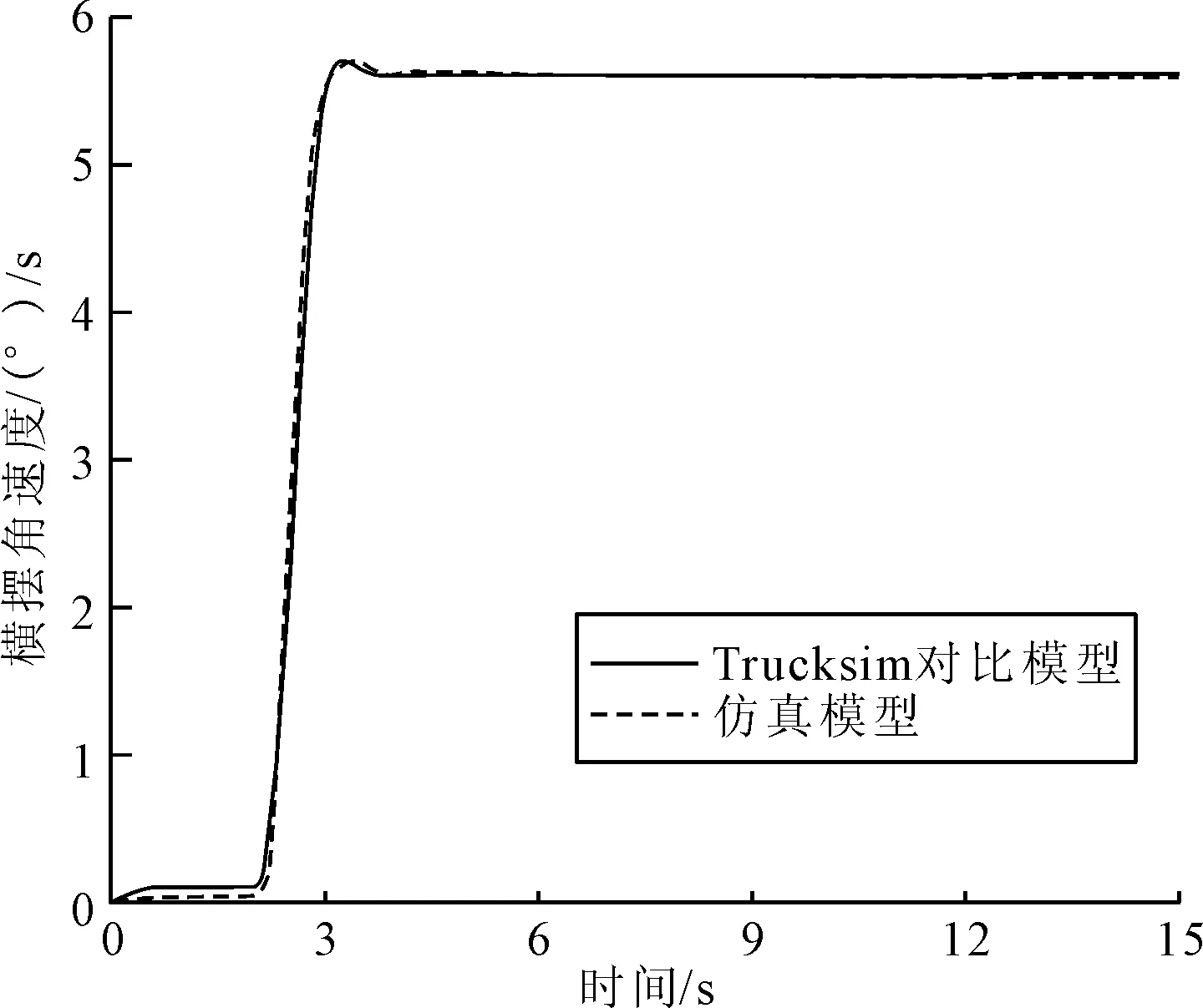
图14 低附着路面横摆角速度

3.2 方向盘转角正弦输入

在Simulink和Trucksim中设置方向盘转角正弦输入信号如图15所示，车辆仿真车速设置为80 km/h，μ=0.85和车速为30 km/h，μ=0.3。

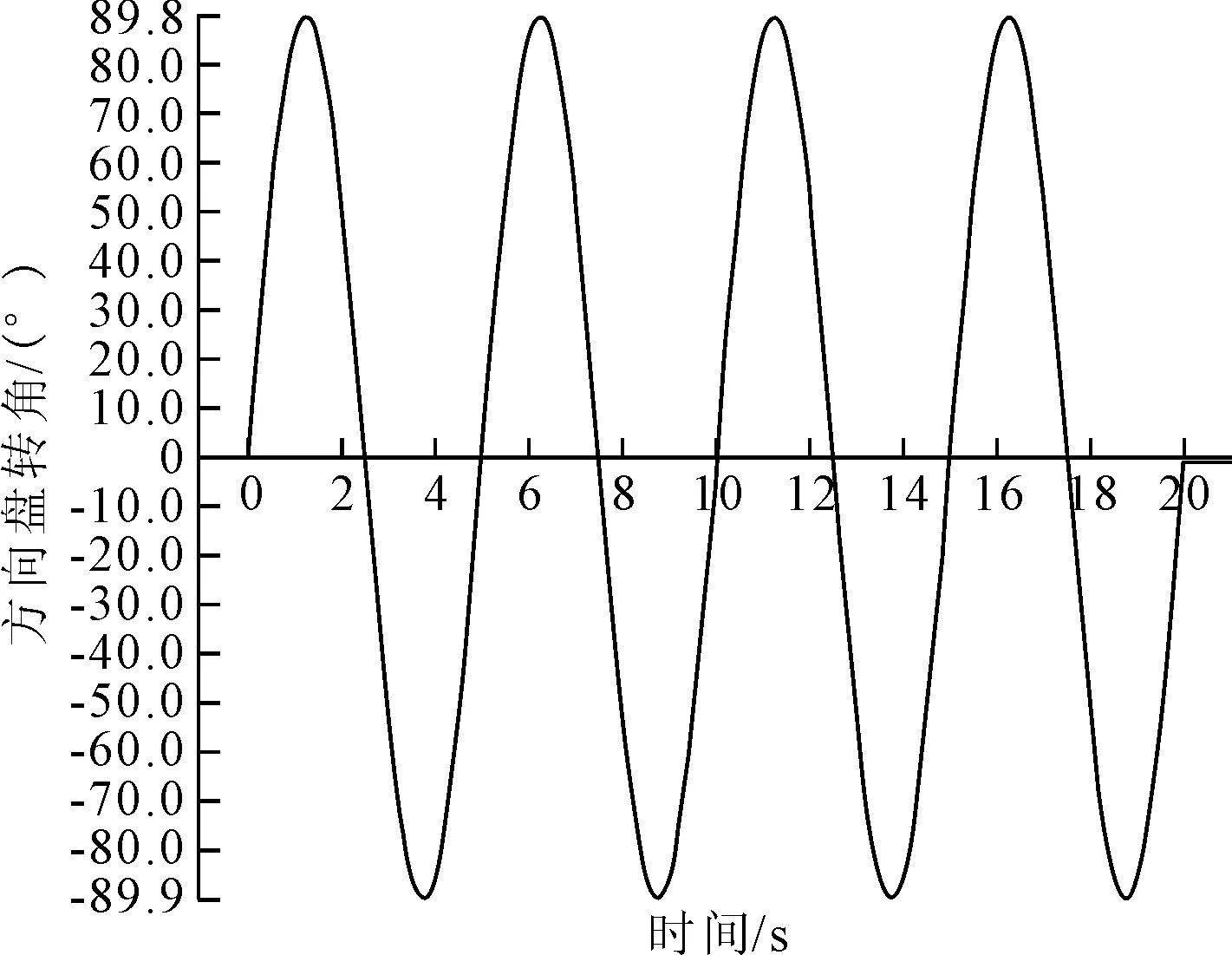
图15 方向盘转角正弦输入信号

3.2.1 高附着路面仿真结果

在高附着路况下仿真后得到侧向加速度与横摆角速度的对比图如图16和图17所示。从图16和图17可知，在高附着路面状况下，仿真模型比Trucksim对比模型的侧向加速度稍慢，但不影响整体模型的走势与峰值。仿真模型的横摆角速度最初有轻微抖动，但整体波动趋势与对比模型一致，且符合方向盘的信号输入走势。

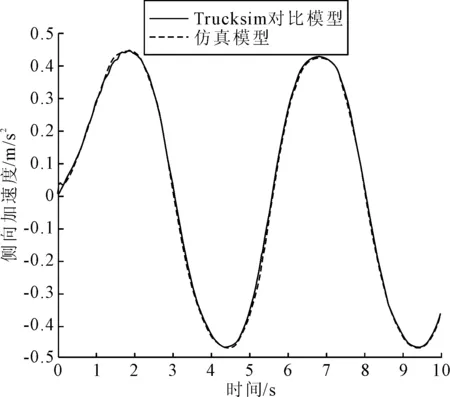
图16 高附着路面侧向加速度

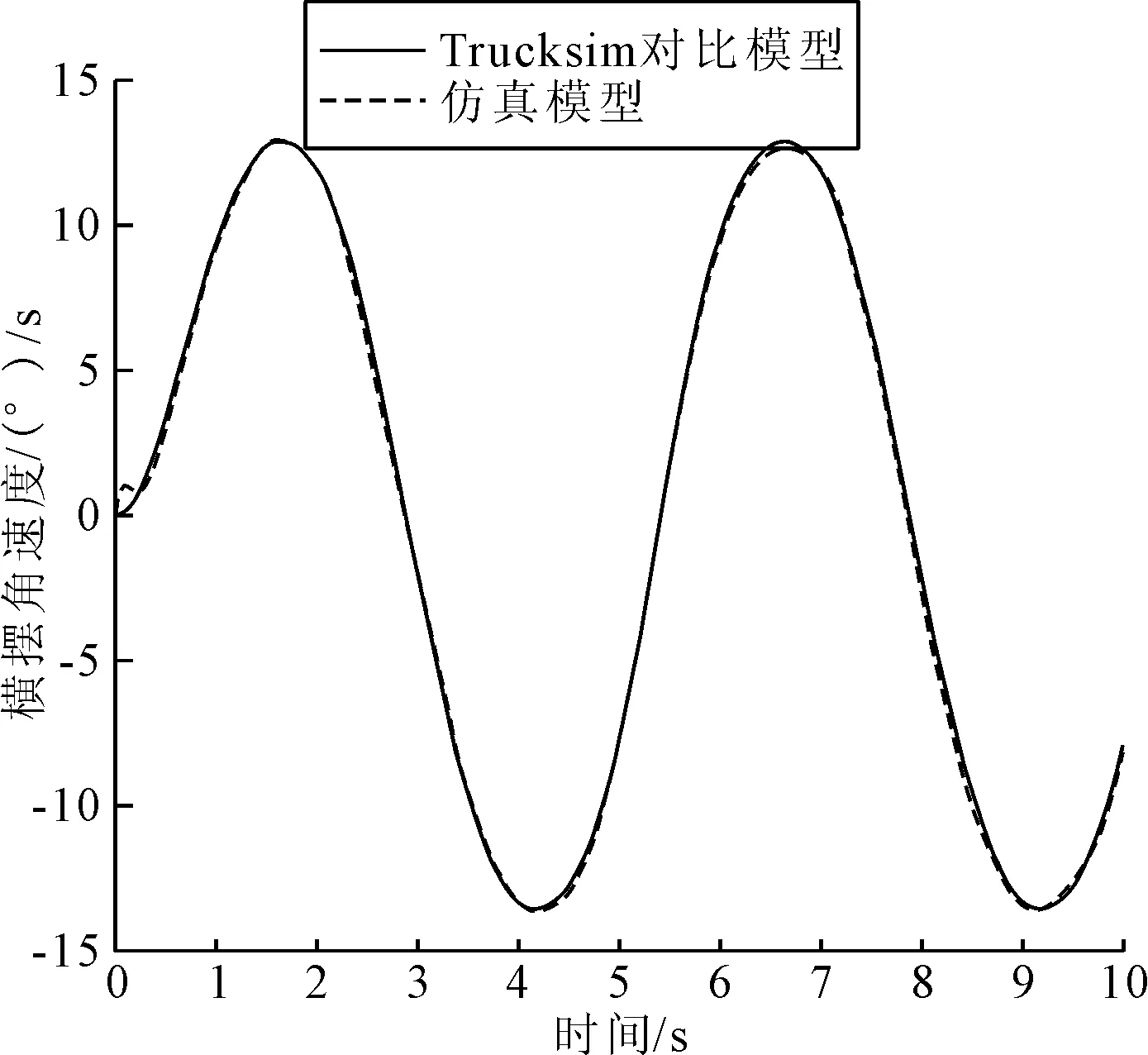
图17 高附着路面横摆角速度

3.2.2 低附着路面仿真结果

当路面为低附着工况时仿真后得到侧向加速度与横摆角速度的对比图如图18和图19所示。仿真模型的侧向加速度与横摆角速度的变化趋势与Trucksim对比模型一致，但初始时的波动略微不同，这是由于在低附着路况下，车辆的行驶状况不稳定所导致的。故虽然初始时的幅度和频率稍有差别，但由于基本走势一致且最终稳定值基本相同，故该模型可为后续研究提供模型基础。

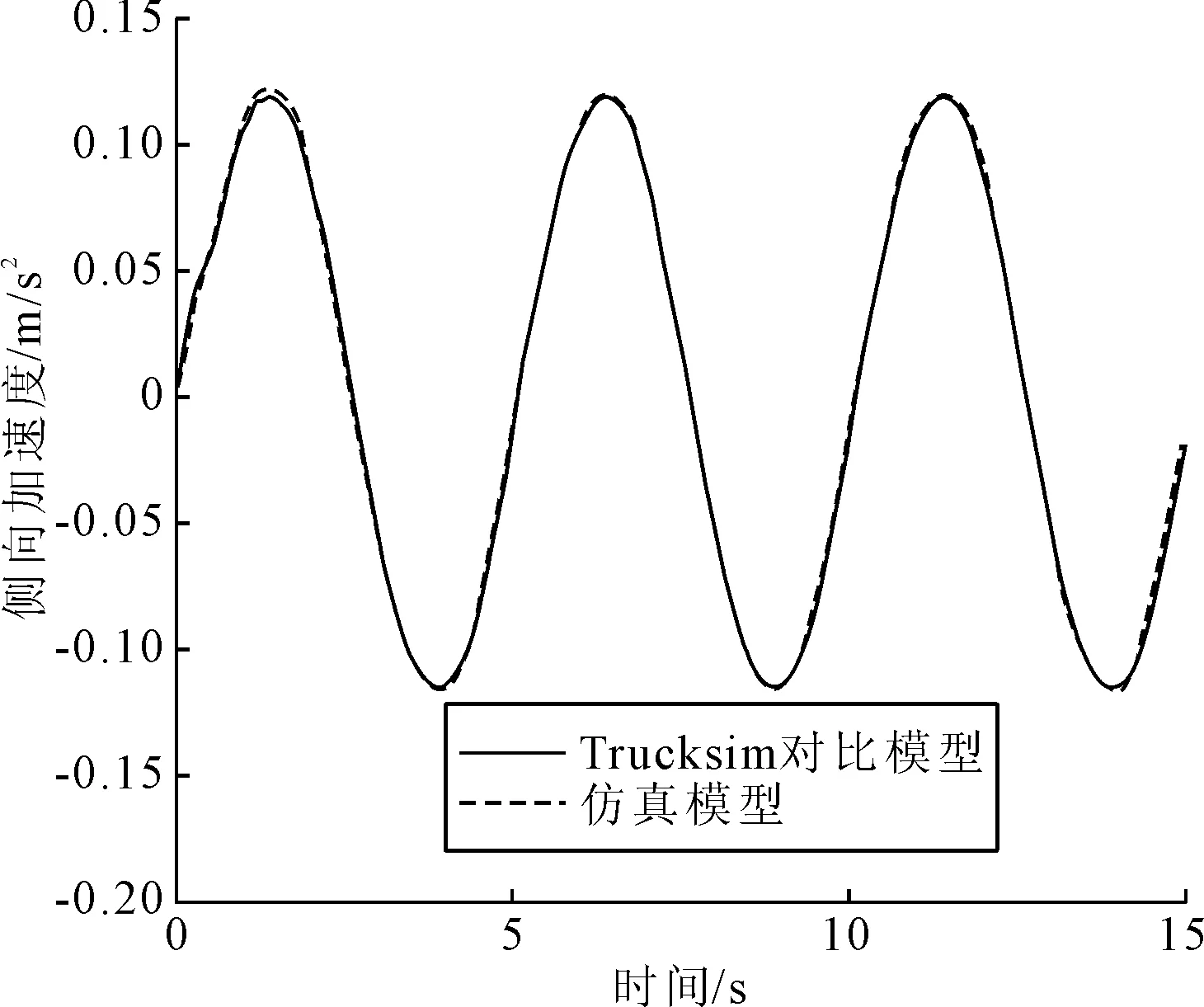
图18 低附着路面侧向加速度

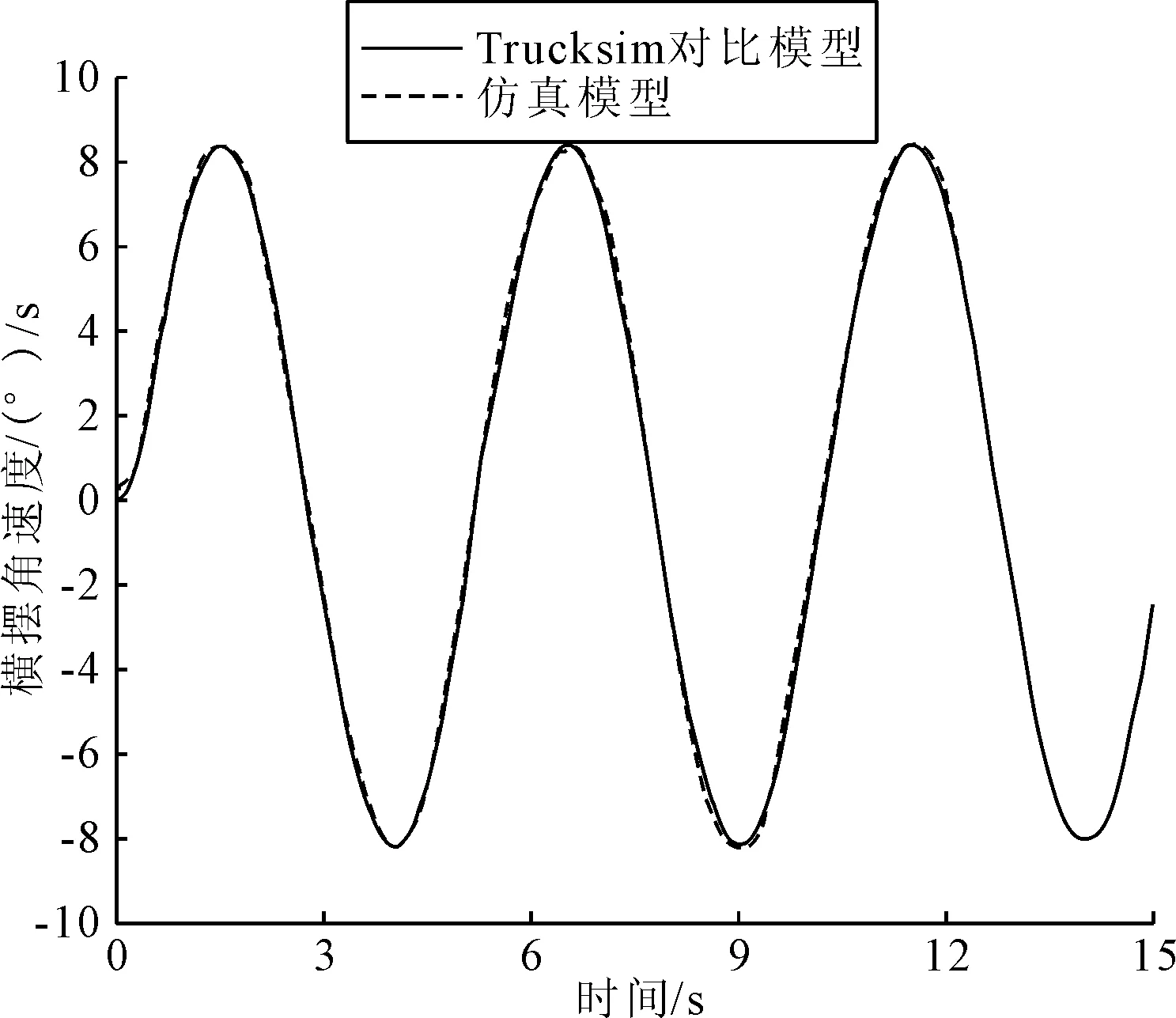
图19 低附着路面横摆角速度

根据仿真结果可知，在不同路面附着条件下，仿真模型的侧向加速度与横摆角速度的走势与变化和对比模型基本一致。以上分析可以得出仿真模型在方向盘转角正弦输入的工况下具有可靠性和准确性。

4 结论

笔者基于大地坐标系与车辆坐标系，搭建了动力学方程，通过Matlab/Simulink软件实现了模块化的整车动力学模型的建立并与Trucksim进行联合仿真。搭建的仿真模型在试验中得到的侧向加速度与横摆角速度的结果与Trucksim对比模型的走势基本一致，且峰值偏差也在合理范围内。因此，所搭建的8×8多轴分布式电驱动车辆的动力学模型具有较高的精度和可靠性，可以为后续的车辆横摆稳定性的控制策略研究提供理论基础，并且可以为控制策略的验证提供模型基础。