汽车万向节十字轴轻量化及其传动轴振动分析

邹 琳，吕文浩，任良顺，徐劲力

(1.武汉理工大学 机电工程学院，湖北 武汉 430070;2.上汽通用五菱汽车股份有限公司，广西 柳州 545007)

十字轴万向节，作为汽车底盘关键零件之一，在底盘传动轴中起到了传递扭矩、转速的功能。随着汽车轻量化技术的广泛应用，十字轴万向节的优化也向着节能降耗低碳的方向进行。杨丽娜等利用ANSYS根据传动轴的受力情况确定其边界条件，然后以传动轴质量最小为优化目标，利用拓扑优化求解最优解，并在同等受力工况下对比优化前后的结构强度，实现汽车传动轴轻量化设计[1]。周成,李理利等用旋锻工艺对等速万向传动轴进行试制，通过改良材料综合力学性能以及空心轴抗扭模量分布，使整轴设计趋于等强度分布，在充分利用材料情形下使强度和寿命满足要求[2]。陈晓红等利用集中质量法建立飞机多十字轴万向节串联轴系扭振分析的等效动力学模型，利用该模型分析中间传动轴刚度和轴间夹角对轴系振动角速度相应、传动精度和传动比的影响[3]。潘宇等以某车型转向系为例，采用ADAMS/view建立了双十字轴万向节的动力学模型，研究以输出轴的转速波动率作为优化目标，对系统中可变参数进行优化设计，得到了理想转向系硬点布置方案，为汽车转向系双十字轴万向节的空间布置提供了参考[4]。李俊虎等基于刚柔耦合多体动力学理论，以有限元软件和多体动力学软件为基础建立双十字轴万向节的刚柔耦合动力学仿真模型分析双十字轴万向节输入轴、输出轴与中间轴夹角大小对传动均匀性的影响，分析结果说明主动轴与中间轴、输出轴与中间轴轴间角的绝对值相差越小，从动轴的转速差值也越小，其转动的不均匀性越小[5]。廖林清等通过分析单、双十字轴万向节运动特性，得到了转向系力矩波动与转向机构平面角与和中间轴万向节的相位角关系，研究表明在转向系统中两万向节相位角和平面角之和为零度或为互补时，转向系的转向力矩波动最小,并设计实车测试数据对比验证了该结论[6]。刘广来等基于MATLAB编程建立了接触变形的分析模型，并基于ANSYS建立了接触应力的分析模型，分析静态下某解放牌载货车用十字轴万向节轴承径向游隙对其接触变形和接触应力的影响，结果表明：十字轴万向节轴承的最佳径向游隙为-0.01～0 mm，最后进行了试验验证，试验结果与分析结果一致[7]。高晋等运用MATLAB对双十字轴万向节三轴共面和异面空间运动规律进行分析，得出了多参数对传动比波动影响的曲线图，并在CATIA中建立与理论推导相匹配的实体模型，同时基于DMU运动分析进行仿真，结果表明，相邻轴之间夹角的差异是导致传动比波动的主要原因[8]。付胡代等利用ANSYS Workbench对十字轴进行应力分析，分析表明十字轴应力集中于两个相邻轴颈的过渡圆角处，依据此结果对轴根过渡曲线进行结构设计，结果表明十字轴轴根采用双曲率型线过渡曲线结构能有效降低十字轴最大等效应力和总变形量[9]。

笔者以国内某万向节生产企业的十字轴万向节的关键零件十字轴为研究对象，对其结构进行轻量化设计并利用ANSYS Workbench分析其应力变化，校核其强度要求。为探究轻量化对传动轴整体的振动影响，建立传动轴弯扭耦合模型，对十字轴进行动力学分析，在理想条件下研究传动轴的振动情况。

1 万向节十字轴轻量化设计

十字轴万向节由主动叉、十字轴、滚针轴承、油封、套筒、轴承盖以及被动叉组成，如图1(a)所示。动力由主动叉轴1传入，从被动叉轴2输出。其工作原理为：主动叉受到转矩驱动旋转带动十字轴运动，在十字轴的物理特性下改变旋转轴向，驱动被动叉旋转，由此改变旋转方向。十字轴是万向节的核心部件，也是万向轴主要的受力部件，它的结构、尺寸以及材料性能决定了万向节的性能，其结构简图如图1(b)所示。

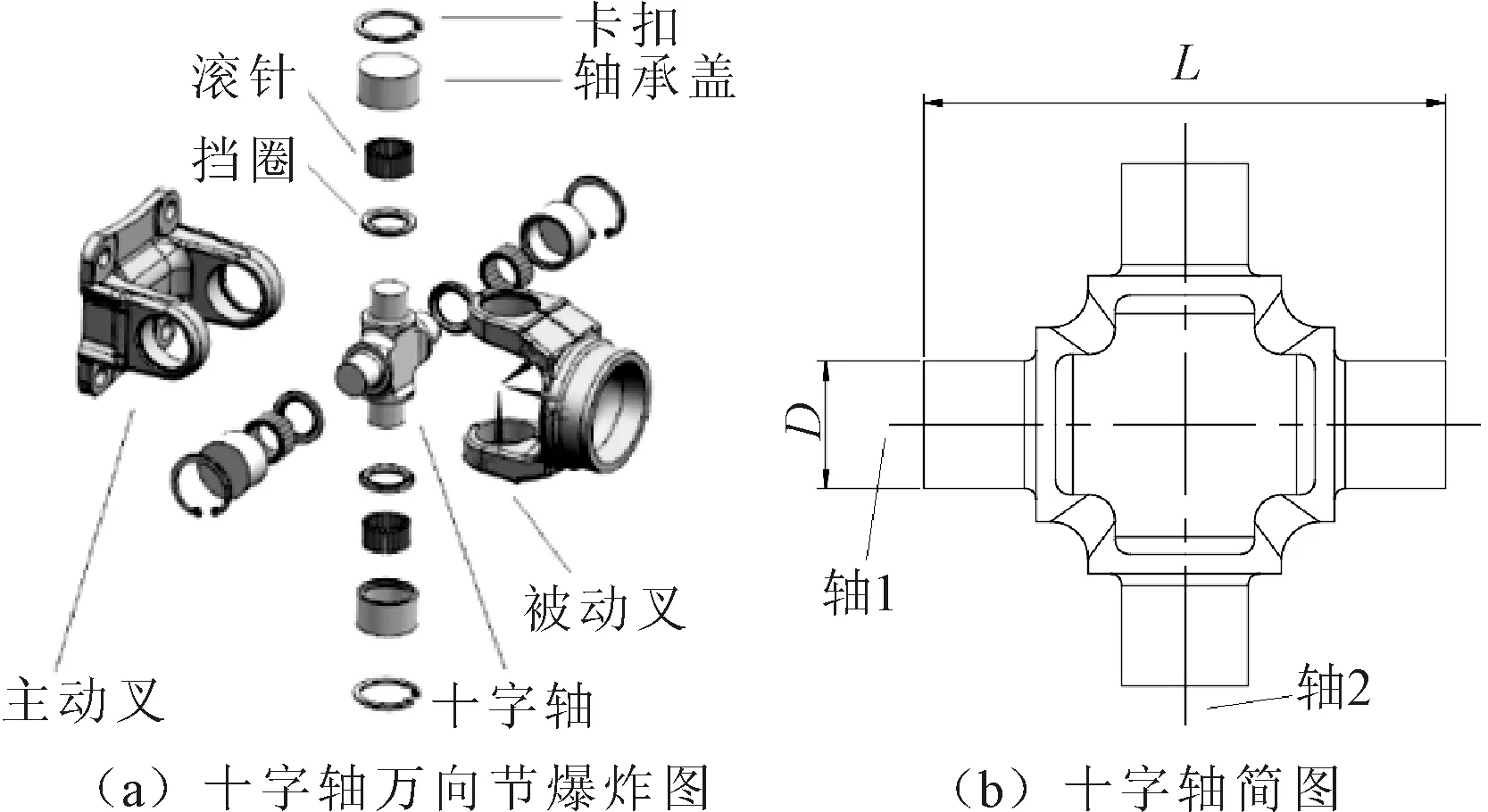
图1 十字轴万向节

本设计以减少质量为目标，在保证强度的前提下，优化了十字轴细节结构及尺寸，减小了优化后的十字轴尺寸，两轴承端面距离L由未优化的76 mm减小为64 mm。十字轴工艺由热锻改为冷挤，减小万向节轴承的滚针尺寸以及优化十字轴轴承的油封，增强油封密封性的同时将十字轴轴承直径D由29 mm下降到25 mm。轻量化前后的工件如图2所示。

图2 十字轴实物图

十字轴失效形式主要有轴颈工作表面出现压痕、剥落及轴颈根部处的断裂[10]。通过对十字轴进行相应的数值分析，能有效预防因前期设计不周而导致的十字轴强度不足断裂等现象的发生。

2 十字轴万向节动力学分析

十字轴万向节的轻量化减小了传动轴系统的整体质量，但在一定程度上影响了传动轴总成的整体振动特性。若优化后的传动轴振动加强，乘客可能会产生不适感，影响汽车的驾驶体验。通过建立传动轴总成系统动力学模型，求解轻量化前后传动轴的振动特性变化。

2.1 传动轴总成系统动力学模型

对传动轴的总成系统建立动力学数学模型，采用系统动力学建模，依据集中质量法，将传动轴总成系统简化为多自由度离散系统。

把传动轴各个结构的分布质量在一些适当的位置集中起来，将质量及刚度均较大的部分视为质量集中的刚体，质量较小的但弹性大的部件视为无质量的理想扭转弹簧和黏性阻尼器。简化后的传动轴弯扭耦合振动模型如图3(a)所示，传动轴UG模型如图3(b)所示。

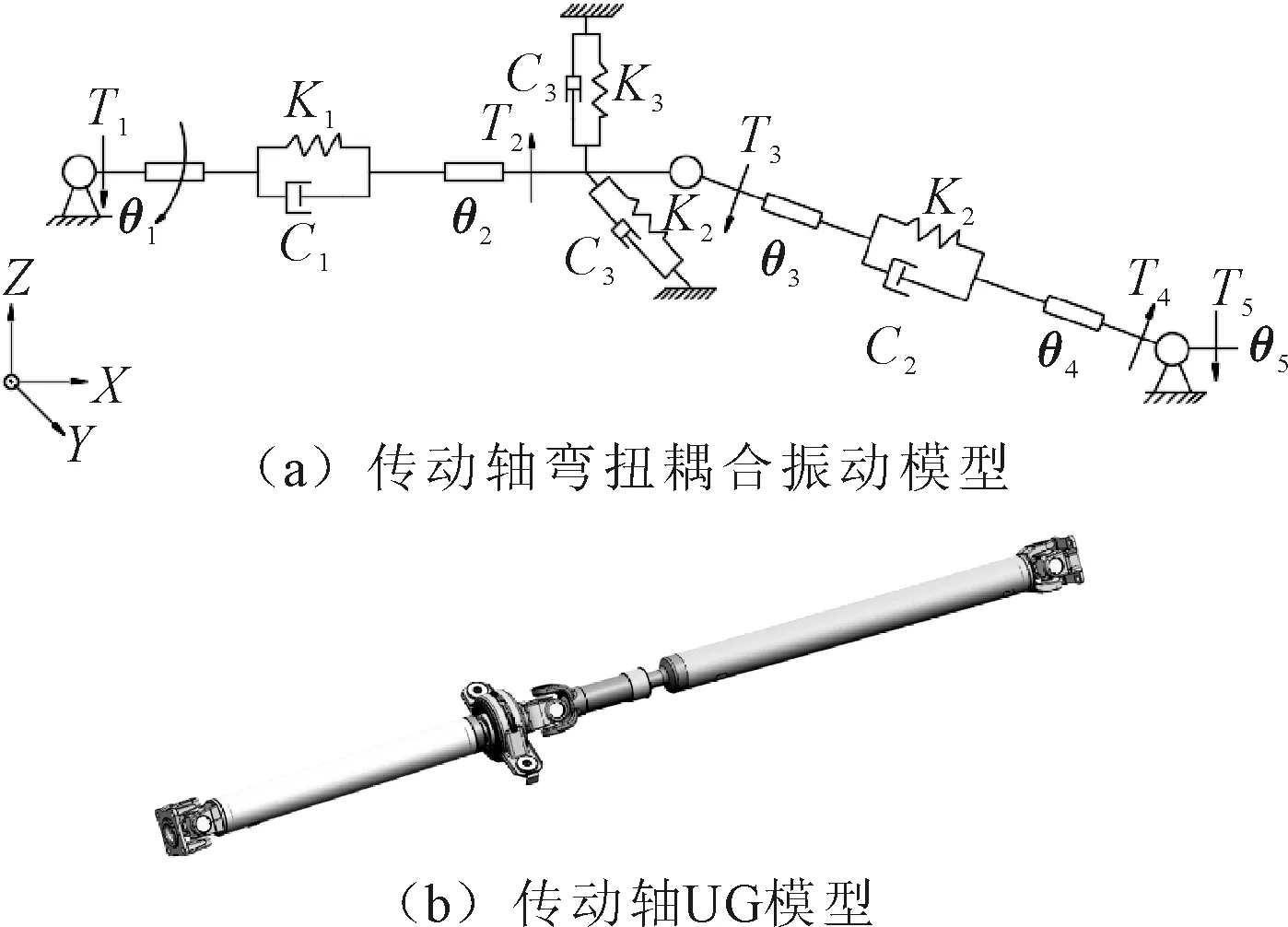
图3 传动轴模型

对照简化模型，结合文献[3]给出的传动轴扭转振动方程，利用拉格朗日方程建立传动轴弯扭耦合振动动力学微分方程如下：

式中：J1、J2、J3、J4分别为传动轴各部件绕其轴线的等效转动惯量；K1、K2、C1、C2分别为中间传动轴轴管和主传动轴轴管的扭转刚度和扭转阻尼；T1、T3为十字轴输入转矩；T2、T4为十字轴阻力转矩；m为传动轴支承处的等效质量；Fy、Fz为支承处y、z向载荷；C3和K3分别为传动轴支承处阻尼和弹簧刚度。

2.2 传动轴动力学方程的求解

在UG中建模，赋予材料属性，利用软件自带的转动惯量计算功能，以两轴管的旋转轴为基准，测量相应转动惯量。传动轴基本尺寸参数如表1所示。

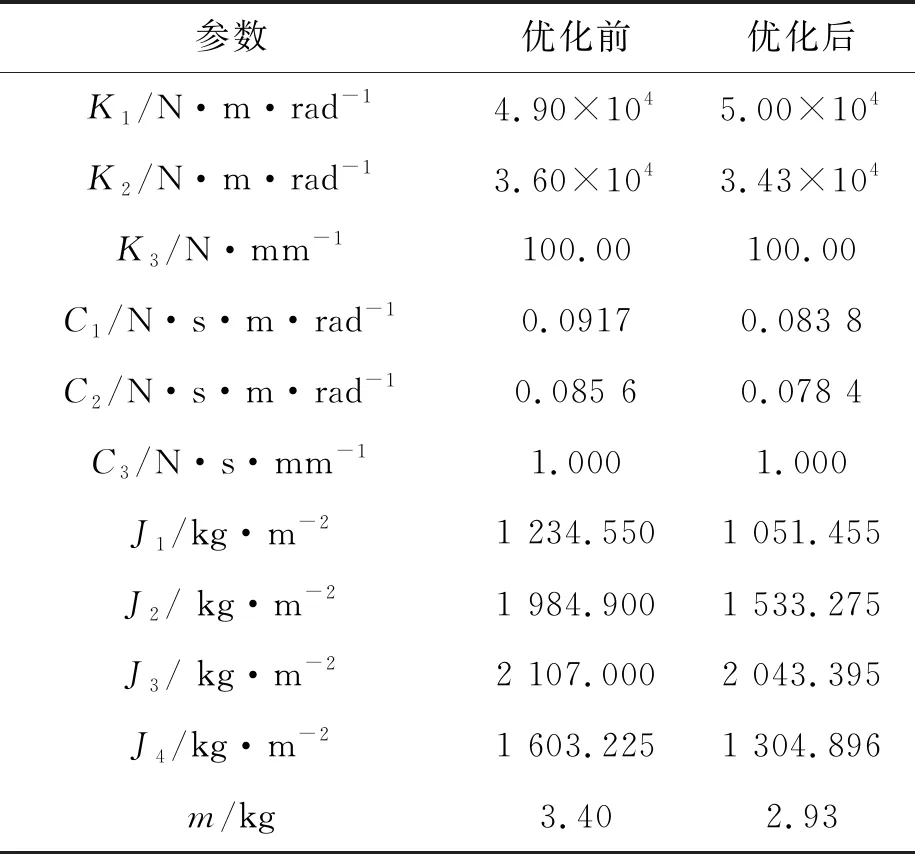
表1 传动轴基本参数

汽车受到来自地面的阻力矩取常值，计算汽车在匀速行驶下，传动轴振动情况。此时，设置汽车的转矩为T1=138.6 N/m，传动轴转速设置为1 800 r/min，即188.5 rad/s。依照传动轴系统动力学方程，编写MATLAB程序，借助龙格-库塔法求解得到优化前后传动轴的扭转振动响应，如图4所示。

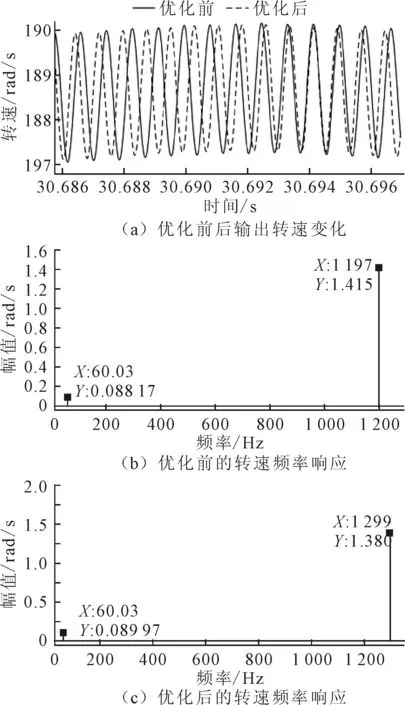
图4 优化前后传动轴的扭转角速度

由图4(a)可知，传动轴优化前后输出的角速度的波动峰值没有明显的区别，传动轴输出转速幅值范围在187～189 rad/s之间,与原有传动轴振动幅度基本一致，波动曲线的频率有所变化。

将转速-时间数据FFT变换后得到优化前后传动轴转速频率响应，如图4(b)和图4(c)所示。图4(b)中 ,频谱线分布在60 Hz和1 197 Hz处，其中60 Hz为发动机波动频率，1 197 Hz为传动轴的频率响应并且幅值较大，在振动中起主导作用。优化后对比于优化前，幅值都略微有所上涨，传动轴频率响应上升到1 299 Hz。传动轴频率上升可能导致与其他零部件振动频率交叉，引起共振，必须要注意与其他零部件的振动频率间隔，避免产生共振。

图5(a)和图5(b)为优化前后传动轴支承y、z两个方向的位移变化，y方向的位移在0.1 mm左右波动，波动幅度为0.1 mm；z方向位移在2.5 mm左右波动，波动幅度在0.2 mm左右。整体上，优化后的传动轴振动要强于优化前；数值上，优化前后的振动差别不大，对汽车平顺性影响基本一致。

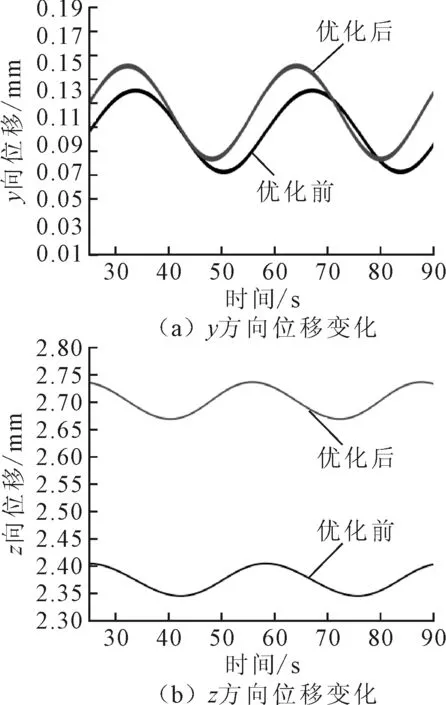
图5 优化前后传动轴支承y、z方向位移

图6为传动轴支承处y、z两个方向的振动加速度变化曲线。两个方向的振动加速度波动幅度都在300 mm/s2以内，优化前后的波动频率几乎没有发生变化。优化后的振动幅度大于优化前的振动幅度。

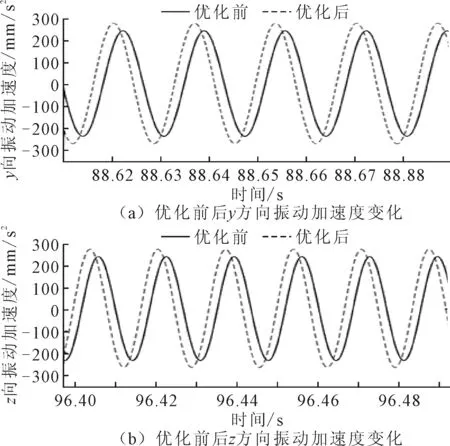
图6 优化前后传动轴支承y、z方向振动加速度

3 结论

笔者首先对万向节十字轴轻量化设计，并通过ANSYS进行强度校核，其次通过建立传动轴的弯扭耦合模型，对十字轴轻量化前后进行动力学分析,求解传动轴的动力特性研究结论如下：

(1)优化后的十字轴，质量及尺寸变小，万向节其他零部件尺寸以及质量相应变化，根据仿真结论，在保持了原有的强度要求不变的情况下，传动轴减少约1～2 kg，最大应力值下降13.2%，最小疲劳寿命增大到6倍。促进整车轻量化，实现节能减排。

(2)传动轴总成在原有动力输入条件下，在优化前后输出的转速幅值无明显变化，维持在187～190 rad/s，波动频率由优化前的1 197 Hz上升到1 299 Hz，可能与其他汽车零部件共振区交叉。在传动轴支承处，y方向的振动主要取决于汽车发动机输出的动力特性，z方向的振动在频率分量60 Hz和1.59 Hz变化较大，使得优化前后幅值的变化有所上升。总体上，十字轴的轻量化使传动轴扭转振动和传动支承处的振动都略微加强，没有造成传动轴总成振动特性过高变化，对汽车的平顺性影响小。