基于有限元分析的乘用车传动轴材料与结构改进

温 艳，孙 轩，姚宇鹏*，刘 普，谢乐春

（1.现代汽车零部件技术湖北省重点实验室,武汉理工大学,湖北 武汉 430070；2.汽车零部件技术湖北省协同创新中心,武汉理工大学,湖北 武汉 430070）

随着我国汽车行业的发展，用户对汽车的可靠性、安全性以及舒适性提出了更高的要求[1]，传动轴的工作稳定性直接影响到整车性能[2]。由于传动轴结构比较复杂，容易引起应力集中的区域较多，而且由于传动轴本身的工作特点，不可避免地存在振动现象[3−4]。为了使传动轴在各工况下能够稳定地传递动力，对传动轴的设计提出了更高的要求。由于传统的传动轴设计方法难以满足其发展需要，而有限元法能够大量减少研究周期和成本，成为了传动轴设计的主要手段。

目前，已有学者采用有限元分析方法对传动轴进行研究。潘宇[5]对某传动轴总成各部件的应力进行分析，发现理论计算与有限元仿真得到的应力值相差较小，该差值主要由节叉危险截面和力作用点的位置造成。王成明等[6]通过台架试验与有限元仿真对比，发现逐渐增大传动轴扭矩时屈服位置出现在轴管端部，而对比结果表明仿真与试验得到的屈服扭矩的误差仅2.27%。鄢强等[7]对最大传动转矩下的传动轴进行静力分析，发现其最大主应力位于十字轴轴管处。Iqbal 等[8]使用欧拉–伯努利方程求解了3 段传动轴的振动频率和模态，应用薄壁梁理论获得其固有频率和模态振型。赵生莲等[9]以某轻型卡车传动轴为研究对象，分析了传动轴在自由模态和约束模态下的振动情况，推导出模态参数与轴管长度和壁厚的线性变化函数，并以此为依据发现减小中间传动轴轴管壁厚能有效提高传动轴总成一阶固有频率。糜健等[10]以某轻型卡车传动轴为研究对象，通过有限元模态分析发现保持传动轴内径不变，增加传动轴的壁厚可消除传动轴的共振情况。尹长城等[11]基于有限元法计算传动轴的固有频率和振型，运用试验模态技术对传动轴进行模态分析，发现传动轴一阶弯曲模态比较容易激发共振。鲁燕等[12]研究发现传动轴的运行工况不稳定性主要是由结构不平衡和材料分布不均匀造成的。

在传动轴的改进方面，选用高性能的材料不仅可以减轻传动轴的质量，而且可以提高传动轴的力学性能。杨畅[13]将传动轴中凸缘叉材料分别替换为镁合金和铝合金后重新进行结构设计，在符合传动轴疲劳和安全系数要求的条件下使凸缘叉质量较材料优化前分别降低72%和56.3%。P.Satheesh Reddy 等[14]研究了复合材料在车用传动轴上的适用性，研究发现在不降低可靠性和满足所有约束条件的情况下，通过优化设计参数，使用复合材料可以大大减轻传动轴的重量。张畔[15]研究发现采用高强低碳微合金钢作为轴管材料不但能提高强度，而且可以减薄轴管的壁厚。除了进行传动轴的材料改进，通过结构改进也可以使得传动轴的性能得到提高。李涛等[16]通过结构改进，使花键轴在满足安全性能的条件下断裂位置可控。刘晓东[17]对凸缘叉、花键轴叉等零件进行结构改进，发现改进后传动轴的强度和刚度基本保持不变，疲劳寿命有所提升，同时实现了各主要零部件的轻量化。

以上工作表明有限元分析方法在传动轴的静力分析和模态分析中有良好的效果，且材料以及结构改进的方法对传动轴的优化十分有效。但只依靠材料改进来满足设计要求会使传动轴的制造成本增加；只依靠结构改进来满足设计要求时，当传动轴中不符合条件的零件过多会使改进后传动轴的整体尺寸出现较大改变，不利于装配和轻量化。基于此，本文以某乘用车传动轴总成为研究对象进行传动轴结构设计，利用Catia 建立传动轴三维模型，并利用ANSYS Workbench 对传动轴的力学性能及约束模态进行分析，根据有限元分析的结果对传动轴中零件的材料进行改进，同时在结构方面做进一步的改进，两者相结合以获得设计成本和制造成本都相对较小且性能良好的传动轴，为汽车传动轴的设计提供参考。

1 传动轴三维模型建立

1.1 车型参数

本次研究的传动轴是基于某乘用车车型参数进行设计的，主要车型参数如表1 所示。

由于发动机和驱动桥之间的距离较长，传动轴的形变会使其原有频率下降，工作时易与车身各总成发生共振现象[18]，因此根据该车型的轴距以及底盘的布置形式，初选传动轴的长度为1 600 mm。由于整体长度大于1500 mm，为了避免共振以及减小噪声，将传动轴进行分段，每根轴的长度初选为800 mm。

传动轴长度由汽车底盘总布置决定，同时也受到由传动轴结构所确定的临界转速的影响，临界转速过低，传动轴更容易发生共振并损害。临界转速由传动轴的尺寸、结构和支撑情况[19]决定。传动轴的临界转速为

式中：nk为传动轴的临界转速，r/min；Lc为 传动轴两万向节中心之间的距离，mm；Dc、dc分别为传动轴轴管的外径和内径，mm。

由于传动轴自身动平衡的误差、花键与花键毂之间存在间隙以及中间支撑的非刚性等，导致传动轴的实际临界转速低于公式（1）所计算的值，因此应引进安全系数K，其中

式中：nmax为 传动轴的最高转速，r/min；nk为传动轴的计算临界转速，r/min；K的取值范围为1.2～2.0。

初选K=2.0，则nk=10 000 r/min，又因3≤Dc−dc≤6，故选Dc=48 mm,dc=42 mm。

传动轴的组成零件中，十字轴和花键轴的尺寸需要根据传动轴的计算载荷来确定，而传动轴的计算载荷由发动机的最大转矩和1 挡传动比来确定[19]：

式中：kd为 猛接离合器所产生的动载系数，取kd=1；Temax为 发动机的最大转矩，取Temax=350 N·m；η为发动机到万向传动轴之间的传动效率，8 挡以上的变速器传动效率为0.9[20]；i1为变速器1 挡传动比，取4.70。

通过计算得到T=1 480.5 N·m。由计算载荷能够确定传动轴总成中十字轴万向节和万向节叉的尺寸，并确立传动轴的模型。

1.2 建立传动轴模型

本次设计的传动轴根据该传动轴的长度和传动轴的计算载荷来确定，其主要参数见表2。

表2 传动轴主要参数

传动轴设计完成后，利用Catia 建立传动轴各零件的三维模型，然后利用Catia 的装配设计模块进行装配，装配后的传动轴如图1 所示。

图1 传动轴总成三维模型

2 传动轴有限元分析

2.1 传动轴有限元模型建立

利用Catia 建立传动轴三维模型后，将其导入ANSYS Workbench 中。模型导入后，在不影响结构功能的基础上进行合理简化[21]，使各零件上划分的网格单元简洁便于计算 。简化对整体影响较小的零部件，以获得质量更高的有限元模型，可以更加迅速地计算出静力学结果[22]。传动轴模型简化的主要内容如下。

1）去除传动轴中各个零件小于4 mm 的圆角、倒角特征，并去除传动轴总成中不参与传递力矩的零件。

2）简化十字轴总成，去除总成中的滚针、油封和防尘罩，将十字轴套筒内孔直径缩小至与十字轴轴颈直径相同以去除两者间的间隙。

3）十字轴轴向不受力或受力很小，在三维模型中去除十字轴轴向卡环[23]。

简化后的传动轴模型如图2(a)所示。

传动轴有限元模型简化后，在Workbench 的材料设置中导入各个零件的材料属性参数。考虑到传动轴轴管的实际用材，本次设计轴管材料选取高强度、低成本和轻量化材料B700QZR[24]。材料属性见表3。

表3 材料属性[25]

在Workbench 中使用六面体网格可以减少同一部件所需的网格数，使得计算结果精度高、易收敛[6]。结合传动轴模型的几何形状，本文采用六面网格划分，网格尺寸选择4 mm，网格单元73263个，网格节点280100 个。传动轴整体网格划分情况如图2(b)所示。

图2 传动轴总成有限元模型 (a) 简化模型，(b) 网格划分

2.2 传动轴静力学分析

对传动轴进行静力学分析时，根据应力、应变情况来判断其在最大扭转载荷下是否会失效。为了使仿真结果符合实际情况，其边界条件依据传动轴台架试验的约束和载荷加载方式设置[6]：在输入端凸缘叉端面施加由发动机最大转矩和变速器1 挡传动比确定的计算载荷1 480.5 N·m，同时在中间支撑装配端面施加固定约束，在输出端凸缘叉端面施加固定约束。

通过Workbench 进行应力计算后，得到传动轴总成的等效应力云图如图3(a)所示，传动轴的最大应力位于花键轴轴颈圆弧过渡处，应力值为634.64 MPa，低于其材料40Cr 对应的屈服强度785 MPa。

图3 传动轴静力分析结果

安全系数云图如图3(b)所示，传动轴的最小安全系数为0.876，位于十字轴轴颈底座根部，十字轴的最大应力高于其屈服强度，因此传动轴在最大扭转载荷下不能正常工作。传动轴各零部件的最大应力和对应的安全系数如表4 所示。

表4 传动轴各零部件最大应力和安全系数

根据QC/T 29082—1992《汽车传动轴总成技术条件要求》[26]中的标准，传动轴零件的安全系数应高于1.5。由传动轴应力云图3(a)和表4 可以看出：传动轴各零件中，十字轴的最大应力高于其材料的屈服强度，不符合设计要求；凸缘叉、万向节叉和花键轴的应力均低于其材料的屈服强度，但其安全系数均低于1.5，不符合设计要求。因此，需要对以上4 个零件进行后续改进。

由传动轴的Y向位移云图得到其在最大扭转载荷下的扭转变形情况如图3(c)所示。切向上最大位移是7.195 5 mm，位置在扭矩施加端凸缘叉的最外部。传动轴的变形量不大，但变形的集中情况比较明显。通过传动轴的扭转变形结果，可求得传动轴的扭转刚度。

零件扭转刚度的计算公式如下[17]。

最大扭转角ϕ：

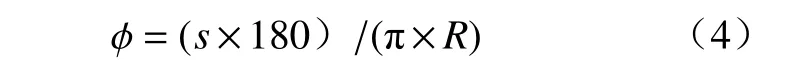
式中：s为 零件的切向最大位移；R为 零件的半径。

最大扭转刚度K：

式中，T为转动轴的计算载荷。

最大扭转变形ψ：

式中，L为 零件长度。

通过式(4)和(5)可得到传动轴的刚度为197.53 N·m/（°），由式(4)和(6)可求得最大扭转变形为4.68（°）/m。而扭转变形一般不大于15 (°)/m[17]，故传动轴的设计满足刚度要求。

2.3 传动轴模态分析

模态分析是研究结构动力特性的一种方法。模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型[23]。为了避免共振，应使传动系统的固有频率避开汽车常用转速范围，并采取有效措施，减小共振振幅，降低共振载荷[2]。本次设计进行模态分析的主要目的是分析得出传动轴总成的固有频率，并与汽车发动机最高转速下的工作频率对比，分析是否会发生共振以及共振时产生的变形量。

进行模态分析时，约束条件模仿传动轴总成在整车上的固定状态，对传动轴总成的输入端、输出端和中间支撑端面进行固定约束[27]，分析传动轴的前六阶模态。图4 为传动轴的各阶模态云图。表5为各阶模态的固有频率以及该频率下的最大变形量。

图4 传动轴各阶模态云图

表5 传动轴前六阶振型及最大变形量

本次设计的传动轴对应车型的发动机为4 缸4 冲程发动机，具体的振动频率如下：

式中：n为 发动机转速；i为 发动机气缸数；τ为 冲程数。

发动机的最高转速为5000 r/min，对应频率为166.7 Hz。由模态分析的结果可得传动轴的前6 阶固有频率都高于发动机频率，因此传动轴不会与发动机产生共振现象。

3 传动轴材料改进分析

上述有限元分析结果显示传动轴的刚度和模态分析的结果均符合设计要求，但其强度不符合设计要求。其主要原因为：在最大扭转载荷工况下，传动轴上十字轴材料的屈服强度过低，导致十字轴失效；凸缘叉、万向节叉和花键轴的最大应力非常接近其对应材料的屈服强度，导致它们在使用过程中失效断裂的概率变高。因此，需要对上述4 个零件进行材料改进。

3.1 材料改进方案

依据参考文献[17]，采用20CrMnTiH 来替换十字轴材料20Cr 和花键轴材料40Cr；采用40Cr 来替换凸缘叉和万向节叉材料45 钢。传动轴各零件的材料属性如表6 所示。

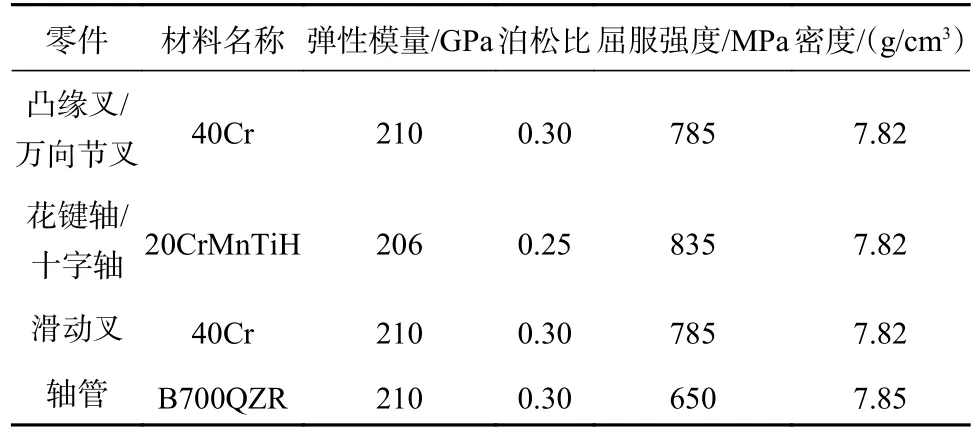
表6 传动轴各零件材料属性

3.2 传动轴的静力分析

材料改进后，传动轴的静力分析结果如图5 所示，各个零件的最大应力及安全系数如表7 所示。

表7 传动轴各零部件最大应力及安全系数

图5 传动轴总成静力分析

由图5(a)可以得到传动轴的最大应力值为634.70 MPa，位于花键轴轴颈圆弧过渡处，同时传动轴的最小安全系数也位于此处。由表7 可知通过材料替换，凸缘叉与万向节叉的安全系数均高于1.5，符合传动轴的设计要求，同时使十字轴的最大应力小于其对应材料的屈服强度。经过材料改进使得十字轴与花键轴的安全系数均有所提高，但两者依然小于1.5。后续改进主要针对十字轴和花键轴。

由图5(c)可以得到传动轴的切向位移为7.1976 mm。通过式（4）、（5）和（6）可以求出传动轴的刚度为197.53 N·m/（°），最大扭转变形为4.68（°）/m。可知经过材料改进后，传动轴的刚度变化不大，材料改进后的传动轴满足刚度要求。

4 传动轴结构改进分析

根据以上有限元分析结果可以发现经过材料改进后，十字轴与花键轴的安全系数不符合要求。由于选取更高性能的材料会使传动轴的制造成本大幅上升，因此后续采用结构改进的方式进一步提高传动轴的性能。传动轴的结构改进基于静力学分析的结果，主要针对十字轴与花键轴进行改进。

4.1 传动轴结构改进方案

根据传动轴有限元分析的结果，其结构改进的目的是减少传动轴的应力集中，提升其强度和刚度，使传动轴的安全系数达到设计要求。

4.1.1 花键轴的结构改进

花键轴的最大应力位于花键轴轴颈的过渡圆角处，可采取增加花键轴直径和花键齿数的方法来增大花键轴的强度和性能[28]。本次改进选择增加花键轴直径的方式来增大花键轴的强度。根据静力学分析的结果，花键轴轴颈圆角过渡处的应力集中情况较明显，故将花键轴的小径由30 mm 增加到32 mm，大径由36 mm 增加到38 mm，如图6(a)所示，花键轴其他部位的结构不变。

图6 花键轴与十字轴的结构改进

4.1.2 十字轴的结构改进

十字轴的最大应力位于十字轴轴颈底座的根部，采取增大十字轴轴颈底座直径的方法来减小十字轴轴颈底座根部的应力。根据静力学分析的结果，十字轴轴颈根部的应力集中比较明显，故将轴颈底座尺寸由24 mm 增加到28 mm，如图6(b)所示，十字轴其余部位的结构尺寸不变。

4.2 传动轴结构改进后的静力分析

结构改进后，传动轴总成的最大应力、安全系数和切向位移分析结果如图7 所示。

图7 传动轴总成静力学分析

根据仿真结果可知，传动轴的应力最大处位于十字轴轴颈底座根部处，最大应力值为555.65 MPa，相比于改进前减小了54.01 MPa。花键轴上的最大应力为514.09 MPa，相比于改进前减小了120.61 MPa。通过结构改进，传动轴上应力集中情况最明显的两个零件的应力都有不同程度降低。传动轴各零部件的最大应力和安全系数如表8所示。

表8 改进后传动轴各零部件的最大应力

传动轴的安全系数云图如图7(b)所示。可以看出传动轴的最小安全系数位于十字轴轴颈处，其大小为1.503，相比于结构改进前增加了0.187。通过结构改进，传动轴的最小安全系数符合了技术要求中安全系数大于1.5 的要求。

传动轴的Y向位移云图如图7(c)所示，最大切向位移位于输入端凸缘叉最外部，其值为6.880 mm。通过式（4）、（5）和（6）可以求出传动轴最大扭转刚度为206.49 N·m/（°），最大扭转变形为4.48（°）/m。对比结构改进前的传动轴扭转刚度197.53 N·m/（°），可以发现通过结构改进的方法不仅减少了传动轴的最大应力，而且还使得传动轴的扭转刚度在原来的基础上增加了8.96 N·m/（°）。

4.3 传动轴改进后模态分析

传动轴结构改进后的模态分析结果如图8 和表9 所示。

表9 改进后传动轴总成模态分析结果

图8 传动轴各阶模态云图

由结构改进后传动轴总成各阶模态振型的固有频率可以看出，改进后传动轴总成的固有频率相比于改进前都有所提升，同时改进后传动轴的固有频率都要比发动机最高转速下的振动频率166.7 Hz要高，因此改进后的传动轴总成也不会与发动机产生共振。

4.4 改进前后传动轴性能对比

针对以上传动轴总成材料与结构改进后的分析结果，与改进前传动轴总成性能进行对比研究，由表10 可知，传动轴改进后最大应力值减小78.99 MPa，传动轴的扭转刚度增加8.96 N·m/（°），传动轴总成的一阶固有频率增加6.80 Hz，下限增加，更适合汽车高速行驶。本文采用材料与结构相结合的改进方法对传动轴进行改进，利用现代传动轴常用的制造材料来改进性能不足的零件，不仅提高传动轴的性能，又保证传动轴的制造成本不会过高。经过材料改进后，传动轴中只有十字轴与花键轴两个零件需要进一步改进。由于继续采用高性能材料会使传动轴的制造成本大幅上升，这时采用结构改进既不会大幅度改变传动轴的整体尺寸，使得其质量不会大幅提高，同时又有利于装配；因此，相较于单一的材料或者结构改进，本次采用的材料与结构相结合的改进方法具有一定的优越性。

表10 传动轴总成改进前后力学性能对比

5 结论

本文利用Catia 建立传动轴三维模型，将简化后的模型导入ANSYS 进行最大扭矩工况下的静力学分析，并进行传动轴的模态分析。根据静力分析和模态分析的结果，对传动轴中的薄弱部位进行材料改进和结构改进，最终得到符合设计要求的传动轴，主要结论如下。

1）静态分析下，传动轴的最大应力为634.64 MPa，位于花键轴轴颈过渡圆角处。传动轴的最小安全系数为0.876，位于十字轴轴颈底座根部，传动轴中凸缘叉、十字轴、万向节叉和花键轴都未达到传动轴技术条件要求的1.5，传动轴的其他零件都符合该要求。对传动轴的模态分析得到其前六阶固有频率范围为200.12～598.88 Hz，高于发动机最高转速下的振动频率166.6 Hz，传动轴不会与发动机产生共振。

2）对传动轴中的零件进行材料改进后，凸缘叉与万向节叉的安全系数高于1.5，符合要求。十字轴的最大应力低于其材料的屈服强度。十字轴与花键轴的最小安全系数有所提升，但是均低于传动轴设计要求的1.5，传动轴的刚度没有明显变化。

3）对花键轴采用增大花键轴直径的方法来减小花键轴的最大应力，改进后花键轴的最大应力值从634.70 MPa 减小到514.09 MPa，最小安全系数从1.316 增加到1.624，达到了技术条件要求。通过增加十字轴轴颈底座直径的方法来减小十字轴上的最大应力，发现改进后十字轴的最大应力从609.66 MPa 减小到555.65 MPa，最小安全系数由1.370 增加到1.503，达到了技术条件要求。

4）通过材料与结构改进，传动轴扭转刚度从197.53 N·m/（°）增加到206.49 N·m/（°），符合设计要求。传动轴的固有频率范围从200.12～598.88 Hz变化为206.92～612.59 Hz，高于发动机最高转速时的频率166.7 Hz，传动轴不会与发动机产生共振。