万向节传动轴动态特性分析及试验验证

牛杰，叶连强，高天芬，王珊，董小忠

万向钱潮股份公司，浙江杭州 310000

0 引言

汽车行驶时传动轴高速旋转，受到周期性的不平衡质量产生的离心力以及发动机往复惯性力的冲击，当附加激振力的频率与传动轴的固有频率接近时，将引发传动系统的共振，表现为剧烈抖动。传动轴共振时的转速即为临界转速，本文结合传动轴材料与结构对其临界转速及万向节受力进行分析，为设计提供理论依据。

目前，传动轴临界转速的计算一般采用经验公式法和有限元分析法。其中经验公式法具有计算简单迅速的优点，因此在传动轴传统设计中被广泛应用。但经验公式法仅对等截面传动轴的临界转速计算效果较好，而对于滑动型传动轴总成，花键轴处截面积较轴管处更小，按经验公式计算误差大，具有较大局限性，且需要进行大量重复的传动轴成品模态试验，无法为前期开发提供较精确的指导。有限元模态分析非常适用于复杂形状传动轴的计算，在现有研究中应用广泛。尹荣栋等采用有限元模态分析校核某传动轴是否会在行驶中产生共振。尹长城等同样采用有限元方法分别计算了分段传动轴的单段自由模态和总成约束模态，提出多段传动轴的振动较大处为中间连接部分。王继红等在子系统基础上，引入带底盘传动轴模型进行模态分析，拓展了造成整车振动和噪声的因素。除此之外，管径、中间支撑刚度对固有频率的影响也在不同文献中被探讨。然而，在以上研究中，几何模型处理、连接关系、接触关系的设置各有差异。本文提出一种有限元模态分析方法并通过试验结果证明其有效性，进一步分析传动轴动态特性，同时作为传动轴的关键结构，万向节在传动轴总成不同临界转速下的动态特性也是本文研究的重点之一。

1 传动轴临界转速分析

1.1 模态分析理论

模态分析是计算结构振动特性的数值技术，结构振动包括固有频率和振型，模态分析就是最基本的动力学分析。要研究万向节传动轴的动态特性，首先要建立该系统的运动微分方程。一般地，动力学方程为：

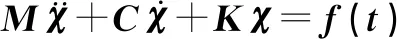
(1)

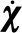
由于结构的刚度特性和质量分布影响结构的固有频率和主振型。系统的无阻尼自由振动方程为：

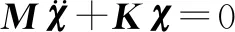
(2)

其对应的特征方程为：

(-)=0

(3)

式中：为系统的固有频率；为模态振型向量。

通过求解式(3)就能得到万向节传动轴的固有频率和振型。

1.2 传动轴临界转速经验公式法

传动轴临界转速的经验公式为：

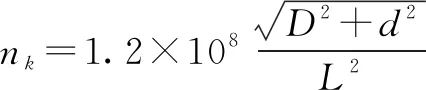
(4)

式中：为轴管的外径，mm;为轴管的内径， mm；为传动轴长度，取两万向节中心距， mm。

由经验公式可知，传动轴临界转速仅与轴管外径、轴管内径和两万向节中心距有关，与传动轴总成材质、质量等因素无关。实际上，两万向节之间的并非只有形状规则的轴管，花键轴叉因结构不规则，用经验公式计算势必会有一定误差，且不同尺寸的传动轴配置，花键轴叉对临界转速的计算结果影响不同。

1.3 传动轴临界转速有限元分析法

在三维建模软件UG中建立传动轴总成模型，包括两端法兰叉、万向节总成、花键轴叉、防尘罩、花键轴、轴管、焊接叉，如图 1所示。之后导入ANSYS中进行前处理。

图1 传动轴总成几何模型

几何处理阶段去除对模态分析基本无影响的防尘罩、万向节总成，并将轴管与花键轴、焊接叉合并。各部件采用10 mm网格划分，传动轴各部位连接和接触行为见表1。

表1 传动轴各部位连接和接触行为

最后，在两端法兰叉的螺栓孔处施加固定支撑约束，求解前6阶模态，其中1阶模态为主要研究目标。传动轴临界转速可由其1阶模态对应的固有频率换算得到：

=×60

(5)

式中：为1阶模态对应的频率，Hz;为临界转速，r/min。

对于具体的接触行为，ANSYS通过不同的接触算法来阻止模型的渗透。常用的接触算法有以下几种：惩罚函数法(Pure Penalty)、拉格朗日法(Normal Lagrange)、增广拉格朗日法(Augment Lagrange)和多点约束法(MPC)。不同算法在算法原理、收敛性和计算精度方面存在一定差异。通过比较不同接触算法的误差，选择更适用于所研究问题的计算方案。

1.4 试验验证

在通过有限元方法进行传动轴模态分析的同时，对传动轴总成采用整车状态下的模态试验，以验证有限元结果的准确性。传动轴总成通常采用基于脉冲技术的瞬态激励测试方法，即“锤击法”，将数据采集器以及加速度传感器组成的临界转速测试系统布置在传动轴轴管上进行敲击测试。按照以上试验方案和装置(图2)，试验测得临界转速平均值为5 690 r/min。

图2 模态试验布置

不同接触算法的计算结果见表2。由表可见，采用MPC接触算法得到的结果与试验平均值误差最小，为6.0%，最适合用于此结构传动轴总成的临界转速计算。这是因为Normal Lagrange和Augment Lagrange较适用于大变形问题中的无摩擦或摩擦接触;Pure Penalty对接触刚度比较敏感，适用于允许具有一定穿透的接触行为;而MPC是点与点之间直接的连接接触，为线性传递关系，因此更适用于绑定接触和不分离约束。除频率外，振型也是判断传动轴共振状态的重要信息。传动轴前6阶模态振型如图3所示，由振型图可知，传动轴低阶共振表现为剧烈的上下弯曲振动。

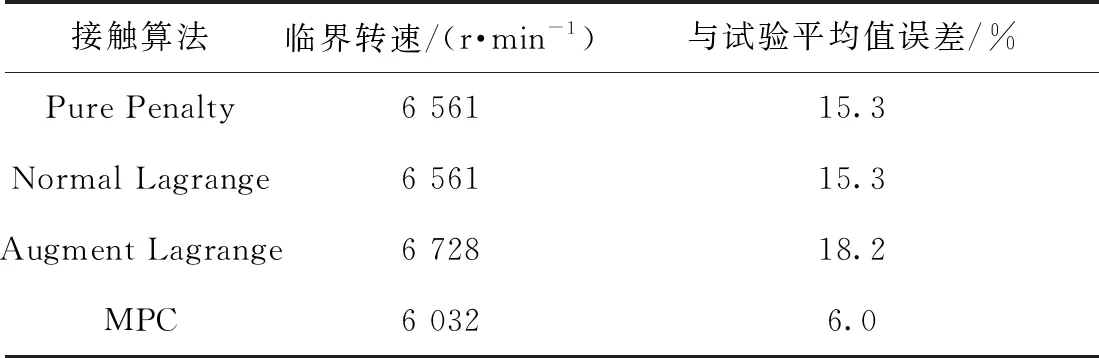
表2 不同接触算法的计算结果

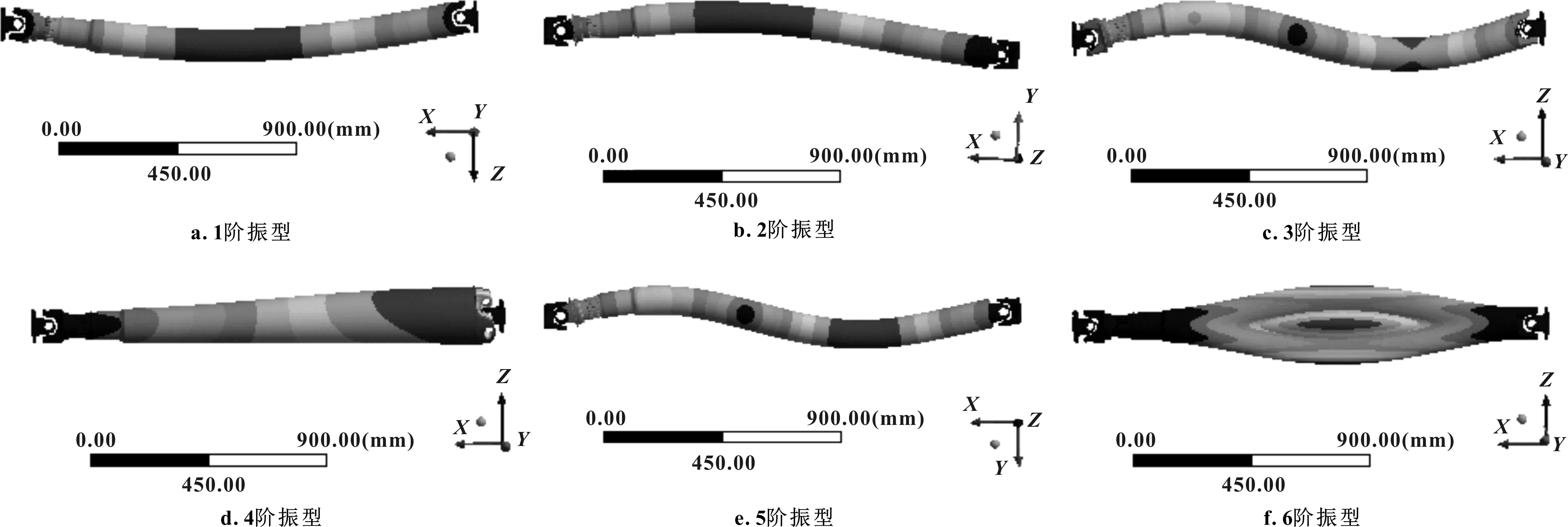
图3 传动轴前6阶模态振型

2 传动轴临界转速影响因素分析

影响传动轴临界转速的因素有多种，如轴管厚度、传动轴长度、中间支撑刚度(多节传动轴)、万向节及花键配合间隙等。本文针对现有模型讨论传动轴长度，即两端万向节中心距对临界转速的影响。

2.1 长度对临界转速的影响

保持其他条件不变，改变传动轴长度分别取1.58、1.63、1.64、1.66 m，计算得到传动轴1阶固有频率见表3。

表3 不同长度传动轴1阶固有频率

根据分析结果绘制传动轴长度与1阶固有频率关系曲线，如图4所示。

图4 传动轴长度与其1阶固有频率关系曲线

由图4可知，传动轴的第1阶固有频率值随其长度的变化分布近似于一条二次曲线，利用数值分析方法对其4个离散点进行曲线拟合，设频率与传动轴长度的关系可用二次方程来表示，则求出的曲线方程为：

=78666-2 6276+2 296

(6)

传动轴长度对临界转速影响较大，传动轴1阶固有频率随着长度减少增大较快。一般而言，传动轴在运行一段时间后，因磨损、变形等因素会引起自身不平衡量加剧，需要传动轴的工作转速不高于临界转速的75%。

2.2 材质对临界转速的影响

长度为1.66 m的传动轴保持其他条件不变，将除万向节以外的其他部件材料换成6061-T6铝合金，计算得到传动轴1阶固有频率见表 4。

表4 不同材质传动轴1阶固有频率 单位:Hz

由表4可知，在传动轴结构不变的情况下，仅改变材料，即使是更轻的材料，对临界转速也基本无影响。

3 临界转速下万向节受力分析

共振状态下，万向节受强烈动载荷，过大的动载荷会严重影响万向节寿命，进而造成总成失效，因此有必要对此时万向节的受力状态做进一步分析。在后处理结果查看法兰叉螺栓孔和花键副两处位置的支点力的向量可间接反映万向节的动载荷受力情况，详细见表5。

表5 传动轴特定部位受力情况

由表5可知，不同传动轴长度下两端固定处和花键副处的受力呈现出明显差异，长度越长，反力越小，万向节受到的动载荷也越小，有利于保证其使用寿命。另外，传动轴材质的改变也会显著影响万向节所受动载荷，传动轴总成更轻的材质可有效降低高速振动工况下万向节轴承受到的激励载荷，有利于提高万向节的使用寿命。

4 结论

(1)通过有限元方法计算了万向节传动轴总成的前六阶模态，确定其临界转速，并与试验结果做对比，发现接触算法中MPC算法最适用于带花键型万向节传动轴总成的临界转速计算，误差仅为6.0%，保证了有限元法的正确性。

(2)系统性地分析了万向节传动轴长度、材质对临界转速的影响，其中传动轴长度对临界转速影响较大，呈现二次非线性关系，而材质的影响则较小。

(3)证明了万向节传动轴总成质量和长度对万向节受力影响较大，其中以质量影响最为明显，因此万向节传动轴总成进行轻量化设计可有效降低万向节受到的外界激振力，从而延长万向节的使用寿命。