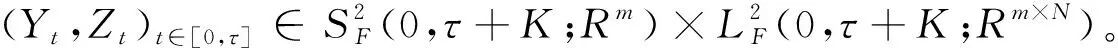马尔科夫链驱动的带停时的超前倒向随机微分方程的适应解

陈 威，李志民，张雪峰

(安徽工程大学 数理与金融学院，安徽 芜湖 241000)

Pardoux等首次提出了倒向随机微分方程(BSDEs)的概念，其形式如下:

-

dY

=

g

(

t

，

Y

，

Z

)

dt

-

Z

dW

，

t

∈[0，

T

]。

Cohen等在此基础上考虑马尔科夫链驱动的BSDEs，证明其适应解的存在唯一性。肖新玲等利用连续性方法研究由马尔科夫链驱动的BSDEs关于初值的比较定理。随后，肖新玲通过迭代法证明了由马尔科夫链驱动的BSDEs解的存在唯一性。Peng等考虑生成元中包含当前和未来时刻解的情况，给出超前倒向随机微分方程(超前BSDEs)的概念，其形式如下:

式中，

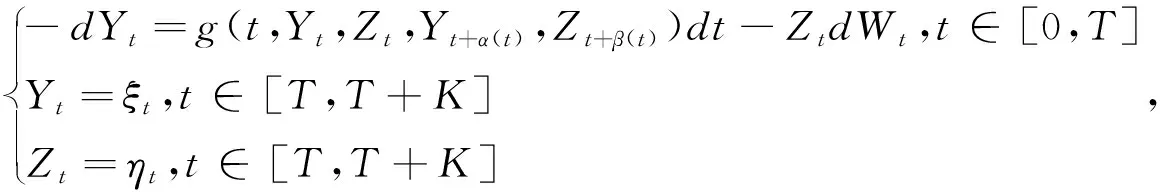
α

(·):[0，

T

]→

R

与

β

(·):[0，

T

]→

R

是满足下面条件的连续函数：(1)存在某一常数

K

≥0，使得对任何

t

∈[0，

T

]，

t

+

α

(

t

)≤

T

+

K

，

t

+

β

(

t

)≤

T

+

K

。(2)存在某一常数

C

≥0，使得对任何

t

∈[0，

T

]以及非负可积函数

f

(·)，

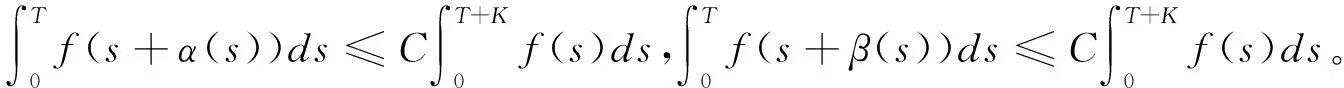
随后，杨哲对其理论做出进一步研究。Lu Wen等在以上工作的启发下，提出如下形式的由马尔科夫链驱动的超前BSDE：

式中，

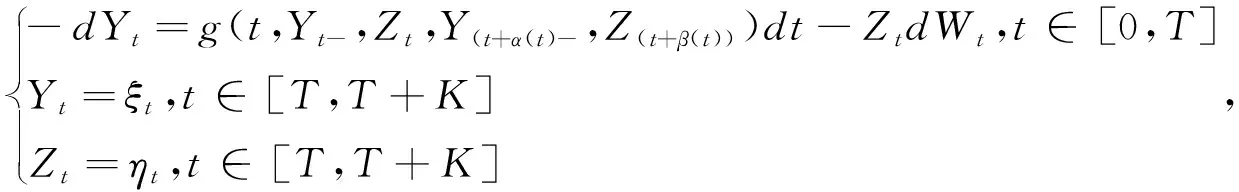
α

(·):[0，

T

]→

R

与

β

(·):[0，

T

]→

R

是满足假设(1)和(2)的连续函数。

由于由马尔科夫链驱动的超前BSDEs的生成元包含当前和未来的解,且有限停时在期权定价中有着至关重要的作用，因此，带有停时的超前BSDEs在金融市场中具有非常广阔的应用前景。吕思宇研究了马尔科夫链驱动的超前BSDEs在金融中的应用。陈增敬考虑终端条件为有限停时，讨论了一类BSDEs在随机区间上解的存在性与唯一性。司徒荣等考虑终端条件为无界停时，讨论了一类BSDEs在随机区间上解的存在性与唯一性。Yang等在超前BSDEs生成元不含Z的超前项这一假设下，讨论了一类带有停时的超前BSDEs解的存在性与唯一性，并得到了一个关于解的逆比较定理。文献[6]考虑由马尔科夫链驱动的超前BSDEs解的存在唯一性。文献[11]在固定时间区间上考虑超前BSDEs生成元中不含Z的超前项。研究在此基础上引发一个猜想：生成元中包含Z的超前项的由马尔科夫链驱动的超前BSDEs在有限随机区间上是否存在唯一解，答案是肯定的。研究尝试通过有限随机区间上的由马尔科夫链驱动的超前BSDEs来解决这个问题，其生成元中包含Z的超前项。研究证明由马尔科夫链驱动的带有停时的超前BSDEs存在唯一适应解。

1 预备知识

设

T

∈[0，∞]，

X

={(

X

)≥0}是连续时间有限状态马尔科夫链。马尔科夫链的状态空间可以用

R

中的单位向量表示为

S

={

e

，

e

，…，

e

}，其中

N

是马尔科夫链上的状态数。(

Ω

，

F

，

P

)是

T

上的完备概率空间，(

M

)≥0是定义在该空间上与马尔科夫链{(

X

)≥0}有关的平方可积鞅，(

F

)≥0是由(

X

)≥0生成的

σ

域流。对任意的

z

∈

R

，‖

z

‖为欧式范数。设

Q

为马尔科夫链

X

在时刻

t

的速率矩阵，定义数量关系如下：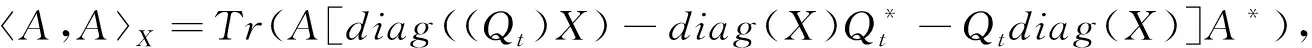

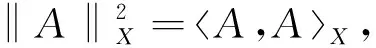
式中，

A

表示

A

的转置。

定义空间如下：

L

(

Ω

，

F

，

P

)={

ξ

；

ξ

是

R

值，

F

是可测的，

E

[‖

ξ

‖]<∞}。

对任意的

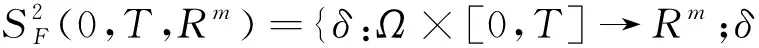
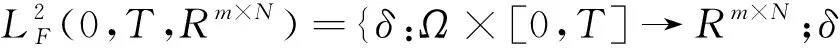
t

∈[0，

T

]，定义

对任意的(

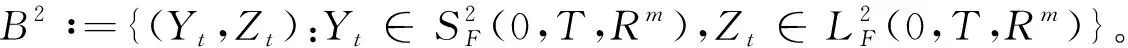
Y

，

Z

)∈

B

，考虑

Y

、

Z

的范数：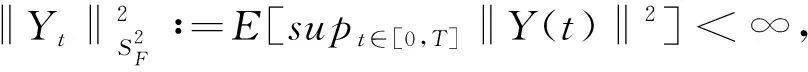

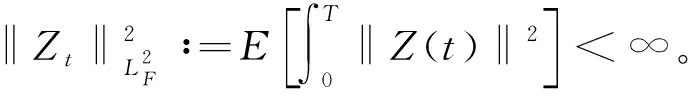
定义(

Y

，

Z

)的范数：

式中，

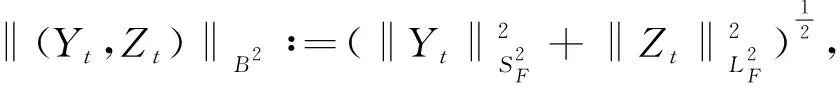
B

是一个Banach空间。设有限停时

τ

<+∞，考虑下面由马尔科夫链驱动的带停时的超前BSDE：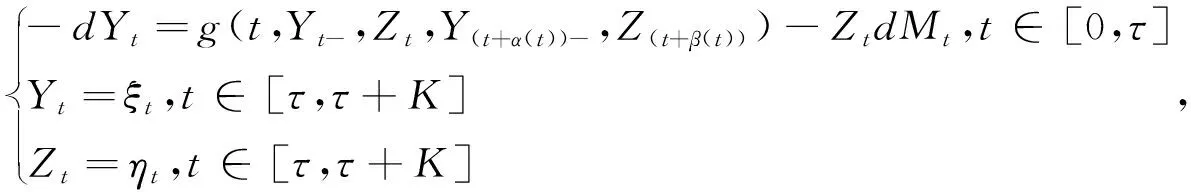

(1)

式中，

α

(·):[0，

τ

]→

R

与

β

(·):[0，

τ

]→

R

是满足下面条件的连续函数：(1)存在某一常数

K

≥0，使得对任何

t

∈[0，

τ

]，(

t

+

α

(

t

))-≤

τ

+

K

，(

t

+

β

(

t

))-≤

τ

+

K

。(2)存在某一常数

C

≥0，使得对任何

t

∈[0，

τ

]以及非负可积函数

f

(·)，

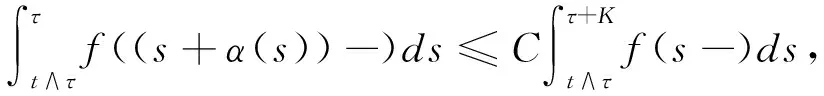
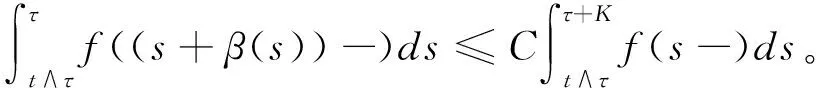
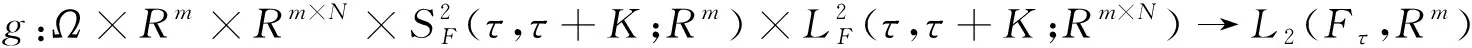
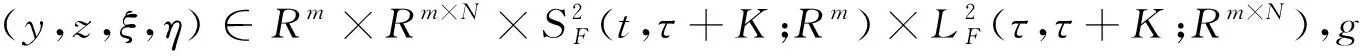
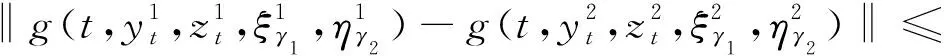
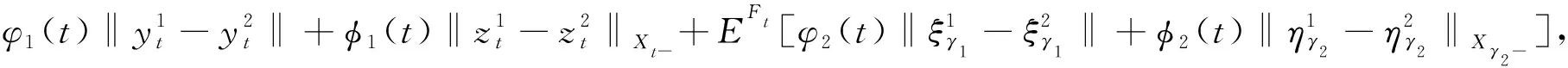
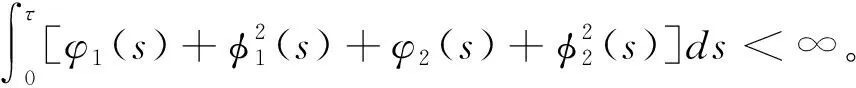
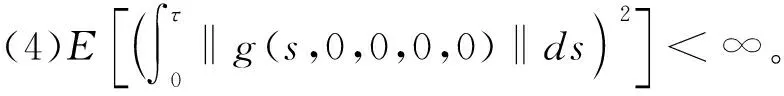
2 解的存在唯一性

考虑由马尔科夫链驱动的带有停时的超前BSDEs。假设由马尔科夫链驱动的带停时的超前BSDEs的生成元满足Lipschitz条件，通过Doob鞅不等式以及不动点定理，证明由马尔科夫过程驱动的带有停时的超前BSDEs适应解的存在唯一性。

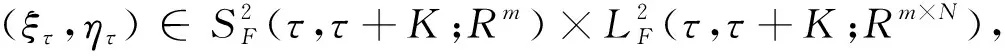
证明

首先，对给定的常数

C

，假设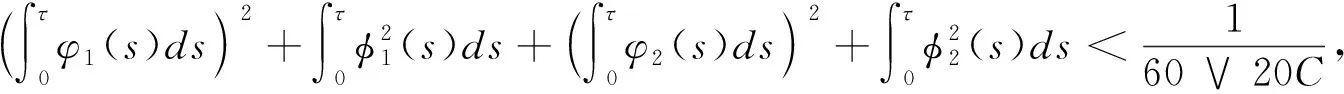

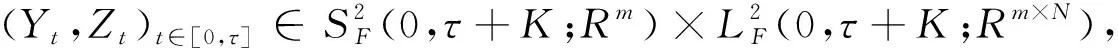
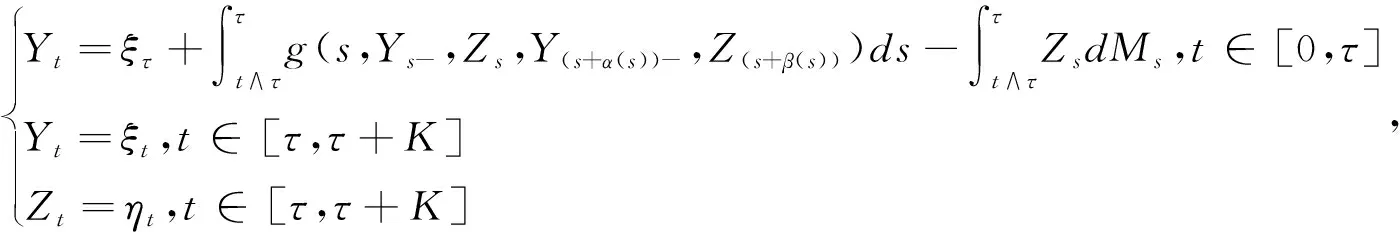
由假设条件(3)可得

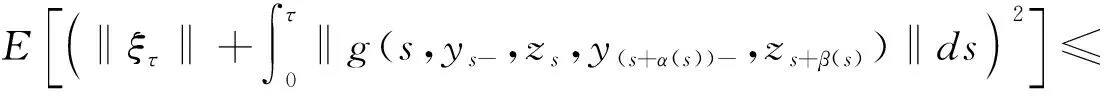
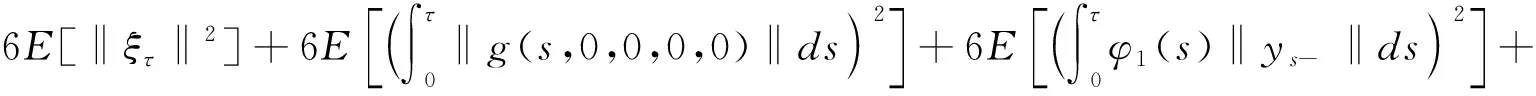
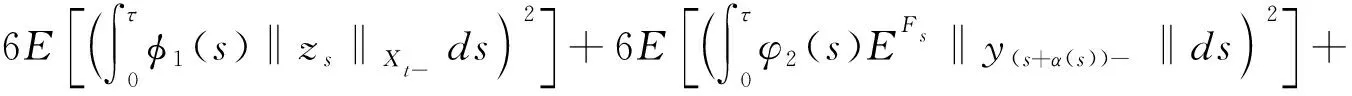
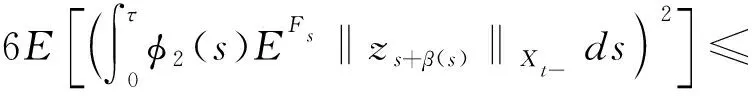
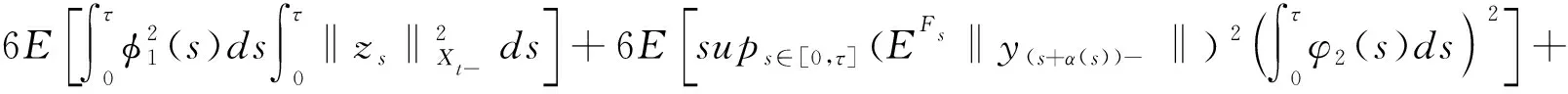
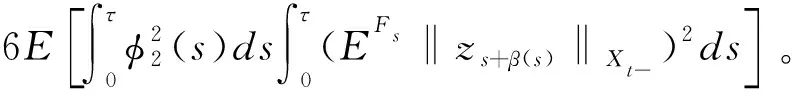
(2)

由Doob鞅不等式可知

E

[

sup

∈[0，](

E

‖

y

(+())-‖)]≤

E

[

sup

∈[0，](

E

(

sup

∈[0，+]‖

y

-‖))]≤4

E

[

sup

∈[0，+]‖

y

-‖]。

(3)

将式(3)代入式(2)可得

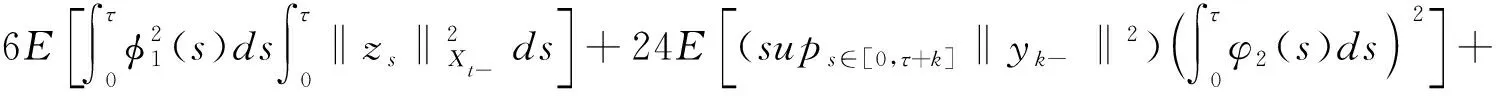
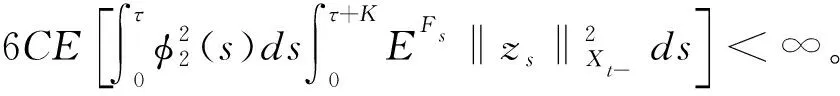
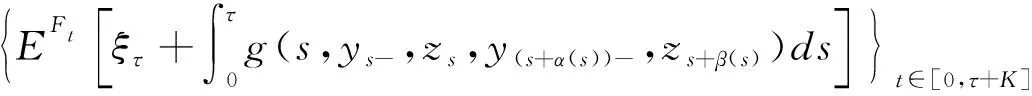
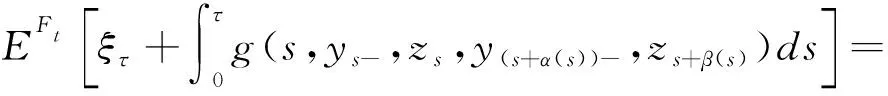
(4)

设

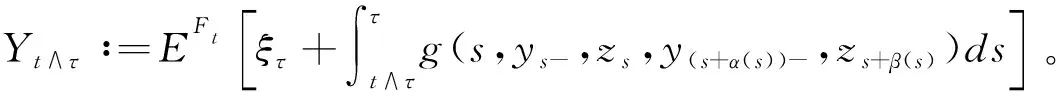
(5)

定义

l

:

B

→

B

是由式(2)、式(3)构造的映射，则

l

:(

y

，

z

)→(

Y

，

Z

)。

(6)

设

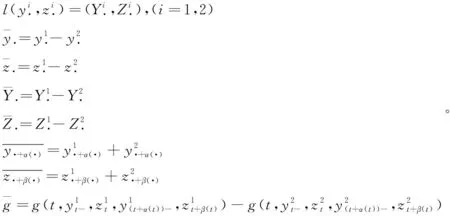
(7)

由杜布鞅不等式和假设条件(3)可得

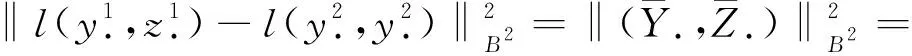
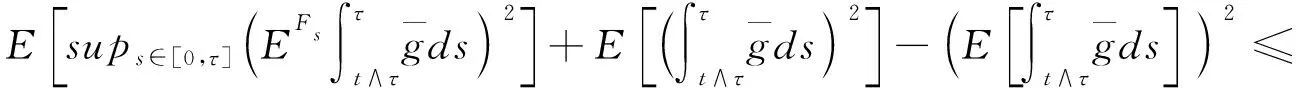
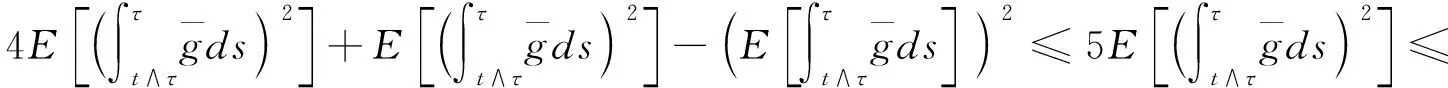
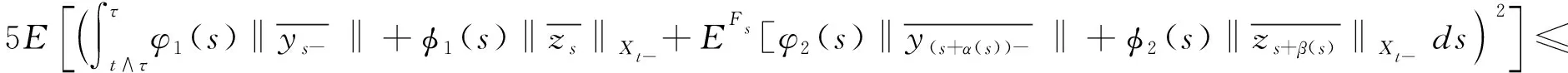
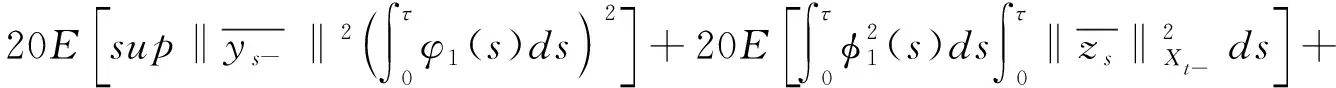
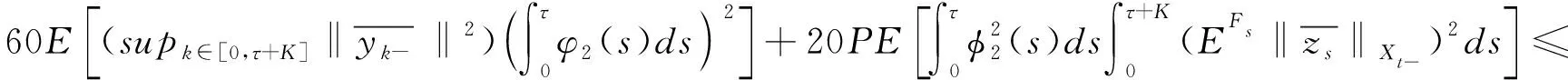
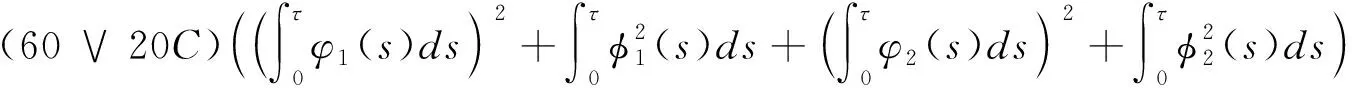
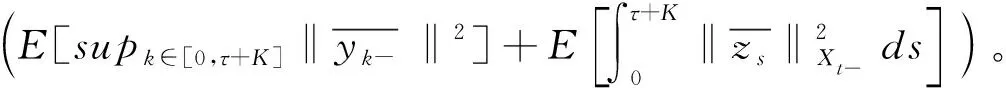
由

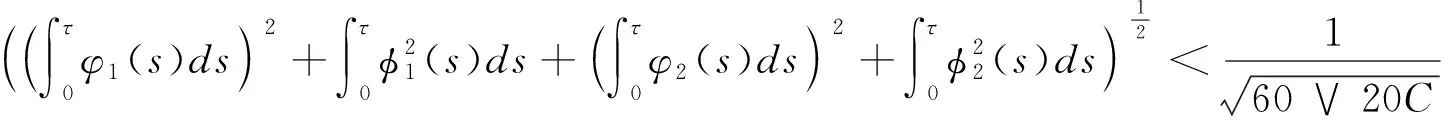
可知

因此，

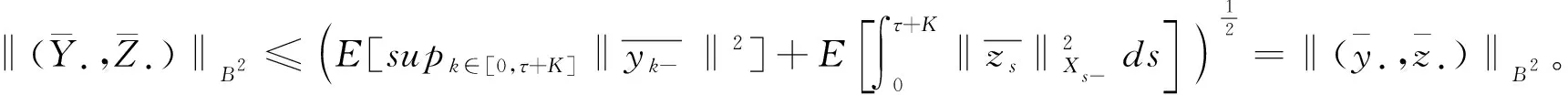
l

:

B

→

B

是压缩映射。由不动点定理可知超前BSDE(式(1))存在唯一解。

由假设条件(7)可知

存在常数

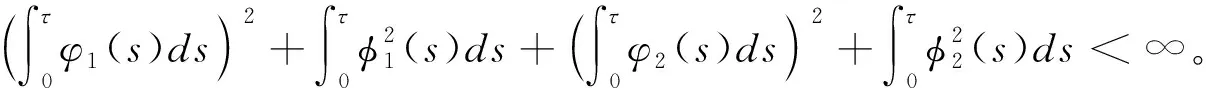
L

使得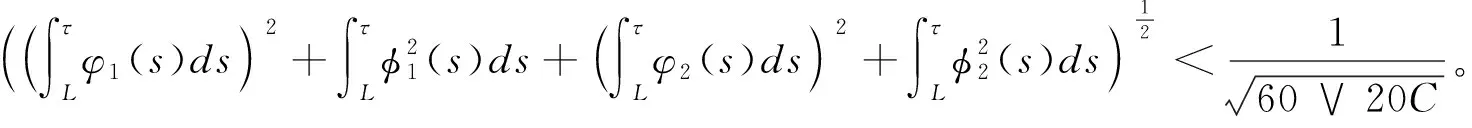

设

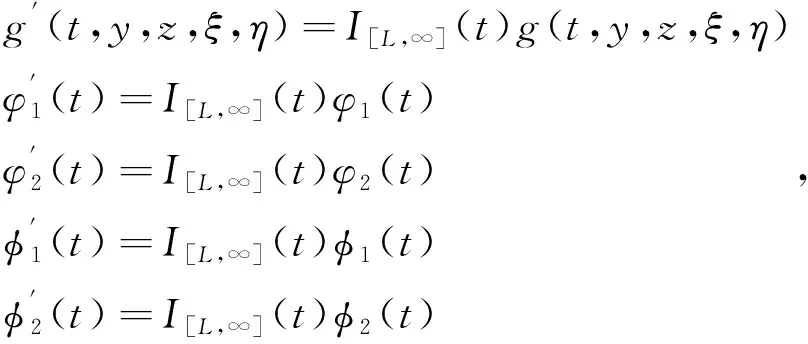
(8)

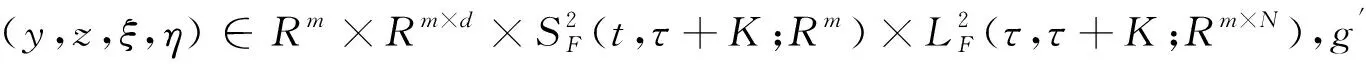
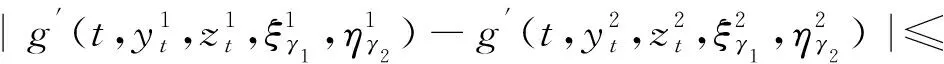
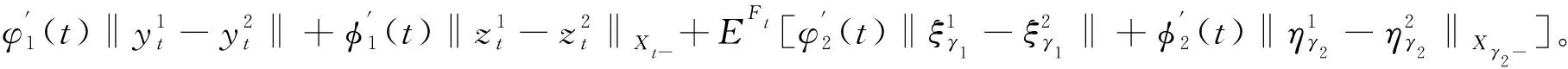
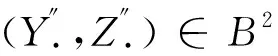
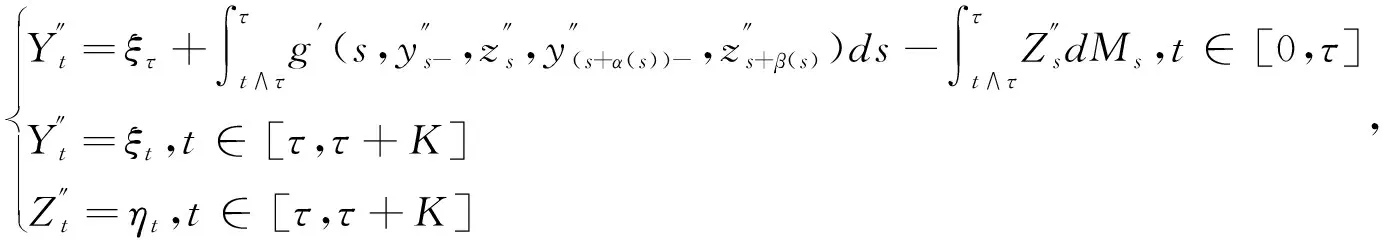
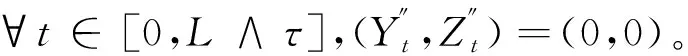
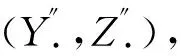
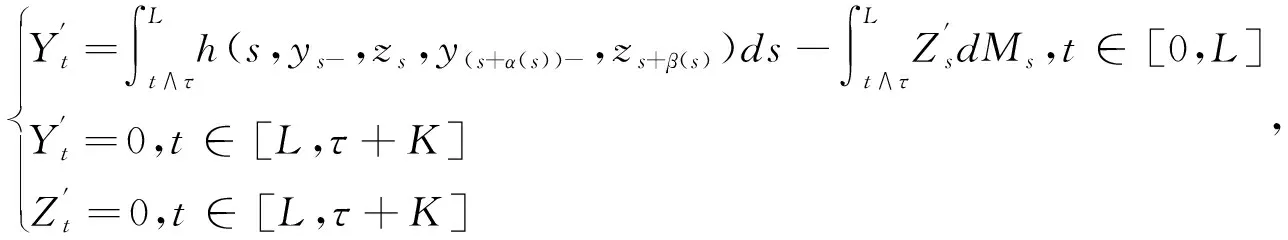
式中，

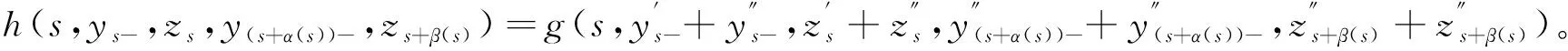
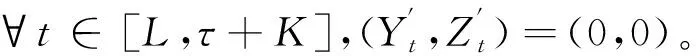
设

对

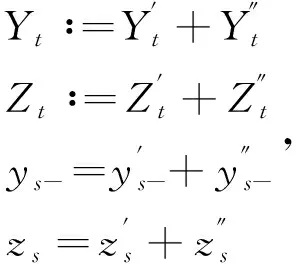
t

∈[0，

τ

]，

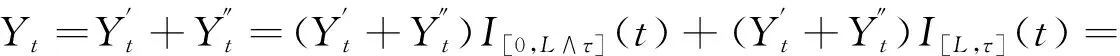
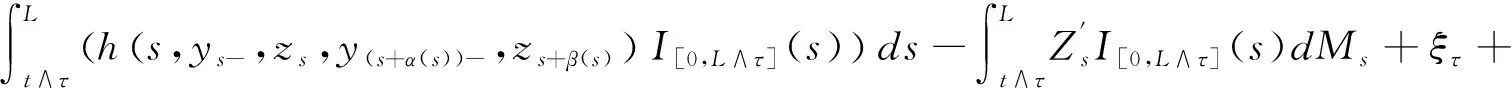
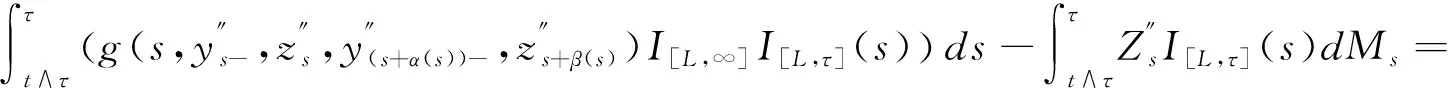
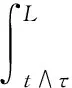
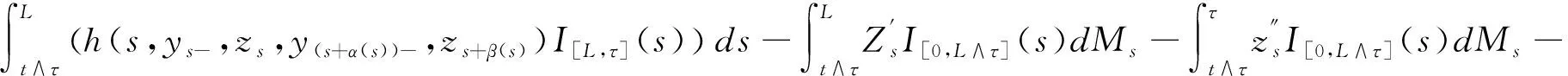
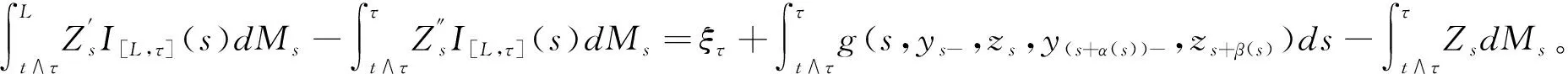
因此，