高分七号卫星控制分系统设计及在轨验证

刘洁 王淑一 陆栋宁 陈超

(北京控制工程研究所，北京 100094)

高分七号(GF-7)卫星是我国民用高分辨率国土立体测绘卫星，以第一颗自主民用高分辨率立体测绘卫星资源三号卫星平台为基础，主要用于完成1∶10 000比例尺有控制点国土测绘任务[1]，是高分辨率对地观测系统中的标志性卫星，也是我国首颗民用亚米级高分辨率光学传输型立体测绘卫星。为了实现高精度的姿态确定，卫星采用与前后视相机一体化安装的甚高精度星敏感器进行姿态确定。为保证载荷工作任务顺利实现，卫星配置了高刚高稳SADA进行太阳翼控制，并通过设计数传天线的轨迹平滑和干扰力矩补偿算法实现高稳定度的姿态控制，以满足测绘和国土资源勘测任务需要。

高分七号卫星于2019年11月3日由太原卫星发射中心发射入轨，入轨时工作在轨道高度为495 km的太阳同步轨道上，其姿态控制分系统是整个卫星系统中最为关键，也最复杂的分系统之一[2]，姿态控制分系统要在卫星运行过程中为有效载荷提供高精度、高稳定度的对地定向卫星平台，同时具有偏流角修正、轨道维持、绕滚动轴的快速侧摆机动、驱动太阳翼对日定向及给数传天线提供指令角度等控制能力。

本文首先对姿态控制分系统进行说明，其次对控制系统方案设计进行详细介绍，包括高精度姿态确定算法、对地定向姿态控制和姿态机动的姿态控制算法，最后给出在轨验证情况。

1 姿态控制分系统简介

高分七号卫星姿态控制分系统由高精度陀螺、高精度星敏感器、太阳敏感器、动量轮、高刚高稳太阳翼驱动机构及推进系统等组成，卫星结构如图1所示。

图1 卫星结构示意图Fig.1 Structure sketch of satellite

卫星姿态控制分系统主要功能包括：星箭分离后，由推力器进行卫星姿态控制，消除星箭分离干扰和太阳翼展开的扰动；建立对地定向姿态后，启动动量轮和CMG；正常情况下由动量轮进行姿态控制，各动量轮工作在标称转速附近，通过动量轮间的协调控制实现整星零动量；在陀螺和星敏感器的高精度定姿方式下，根据载荷成像任务需求，可由CMG和动量轮控制实现绕滚动轴的快速侧摆机动；根据地面指令可进行轨道机动控制，并满足机动期间姿态控制指标要求。正常轨道运行期间，卫星根据模拟太阳敏感器输出或者太阳翼转角输出，进行太阳翼指令角速度计算，实现太阳翼对日跟踪；在卫星与地面站互见弧段，可为数传天线提供指向控制的指令，实现天线对地面站的捕获与跟踪。

卫星要实时进行太阳翼的驱动控制，且太阳翼较大，因此整星的动力学以中心刚体+两个挠性附件[3]描述为

(1)

(2)

(3)

(4)

(5)

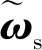
2 控制分系统方案设计

2.1 控制分系统方案设计的特点

高分七号卫星控制分系统方案设计的主要特点是实现高精度的姿态确定、高稳定度的姿态控制和快速姿态机动控制。为了实现卫星的高精度姿态确定，设计了基于载荷的一体化安装布局方式和星敏感器间相对安装误差标定算法，并可以在地面通过采用前向实时卡尔曼滤波算法分别对载荷姿态分别进行事后高精度姿态确定。为了实现卫星的高稳定度姿态控制，首先考虑轨道进动的轨道角速度计算，提高了卫星偏航轴姿态控制精度；通过数传天线的转角平滑和干扰力矩前馈补偿大大减小了数传天线预置和跟踪过程中对卫星稳定度的影响；通过采用高平稳太阳翼驱动机构，大大提高了卫星的姿态稳定度。为了实现卫星的快速侧摆机动，采用剪刀式构型的控制力矩陀螺，并设计了姿态机动过程中的轨迹规划算法，减小了机动过程中的挠性振动的影响。

2.2 高精度姿态确定算法

2.2.1 基于载荷的高精度姿态确定方案

卫星配置两台双线阵立体测绘相机，前视相机视轴方向为卫星本体系+Z轴绕本体系+Y轴转动+26°后确定的坐标轴方向，后视相机视轴方向为卫星本体系+Z轴绕本体系+Y轴转动-5°后确定的坐标轴方向。

为了提高卫星的姿态确定精度，卫星采用单探头测量精度优于1″(3σ)的甚高精度星敏感器[4]，并且将其中两个星敏感器与前视相机一体化安装，另外两个星敏感器与后视相机一体化安装的安装布局(见图2)。

根据卫星高精度姿态确定需求，利用星敏感器和陀螺联合定姿方式进行姿态确定，针对星敏感器和陀螺的噪声特点，设计了常系数、低增益的卡尔曼滤波算法。该方法易于星上实现，且充分利用陀螺短期测量精度高的特点，实现高精度姿态确定。卫星星上高精度姿态确定选取3个正交陀螺进行姿态预估，选取前视相机上安装的甚高精度星敏感器的数据进行卡尔曼滤波姿态修正。

卫星下传各个星敏感器数据，地面根据高精度陀螺数据和星敏感器数据，采用前向实时卡尔曼滤波算法分别对前视相机的姿态和后视相机的姿态分别进行事后高精度姿态确定，事后长期的惯性系姿态确定精度优于1.5″(3σ)。

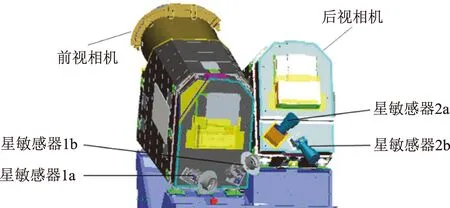
图2 卫星星表布局示意图Fig.2 Configuration sketch of satellite

2.2.2 相对安装误差标定算法

针对入轨后星敏感器安装变形以及存在地面测量误差的情况，设计了星敏感器间相对安装误差标定算法。星敏感器间安装误差的标定原理为同一时刻不同星敏感器的测量应该满足相对安装关系。卫星上可以指定任意星敏感器j为基准星敏，对其他星敏感器i的安装矩阵进行了修正。一般各星敏之间的安装误差较小，星上按照1、2、3转序求出星敏感器i相对星敏感器j的滚动轴、俯仰轴和偏航轴安装误差角φi,θi,ψi。考虑到星敏感器噪声影响，对标定误差角进行滤波。鉴于后视相机的基线较短，有利于地面标定精度，因此在轨选取与后视相机一体化安装的星敏感器进行基准标定。通过对星敏感器相对安装偏差的标定，提高了星敏感器姿态确定精度。而对于基准星敏感器的安装偏差，可利用地标点的标定，对星敏感器和载荷间的系统类偏差进行统一修正。

2.3 对地定向的姿态控制

1)考虑轨道进动的轨道角速度计算

为了提高偏航轴的姿态控制精度，采用考虑轨道进动的轨道系相对于惯性系J2000.0的角速度ωOI计算公式为

(6)

式中：ωo为轨道角速度，u为卫星幅角，i为轨道倾角，Ω1为拟平升交点赤经的一阶长期项系数。

2)高刚度高稳定度SADA进行太阳翼控制

以往的卫星采用的步进电机型太阳翼驱动机构(SADA)，对卫星太阳翼挠性模态的激励较大，对卫星稳定度有一定的影响[5-6]。为了解决该问题，采用以扰动力矩较小的永磁同步电机作为驱动源，设计了高刚度高稳定度太阳翼驱动机构[7]。高分七号卫星采用的高刚度高稳定度太阳翼驱动机构，其稳态跟踪模式下的驱动不平稳性优于5%，大大提高了卫星的三轴姿态稳定度。

3)数传天线的转角轨迹平滑

卫星一般安装有多副通信天线，每副天线一般具有两个或以上的转动自由度。首先，天线的多轴运动持续改变整星的质量分布，使卫星姿控性能受到影响，对星体各轴均存在扰动影响；其次，天线的指向运动不是匀速运动，不同转速范围对星体稳定度的影响有很大区别，转速越大姿态扰动越大，因此天线的指向运动对星体姿态控制产生了很大的扰动影响[5]。为了抑制数传天线预置和跟踪过程中对卫星姿态的影响，高分七号卫星采用了数传天线轨迹平滑和干扰力矩估计，并进行前馈力矩补偿，在轨应用证明明显改善了天线运动对卫星稳定度的影响。

为了降低天线跟踪前(预置)由于天线加速度对星体稳定度影响，拟对天线运动轨迹进行平滑处理(见图3)。天线对动目标的捕获轨迹规划，其主要思想是在给定的天线运动角速度和角加速度幅值约束条件下，根据天线指令转角的变化，以及当前转角与理论转角的偏差，计算下一周期的期望转速。其中，一方面为了降低当前转角与上一周期理论转角偏差较大时可能引起较大的转角补偿量导致冲击过大，另一方面也为了提高当前转角与上一周期理论转角偏差较小时尽可能加大转角补偿量，使得误差收敛速度足够大，针对上述两方面的考虑引入了转角偏差的自适应转角补偿策略，即根据转角误差大小适时调整增益系数，从而使得天线对目标的捕获过程既保证快速性，又具有平滑性，以避免激发附件振动模态，有效降低对整星姿态的冲击影响。

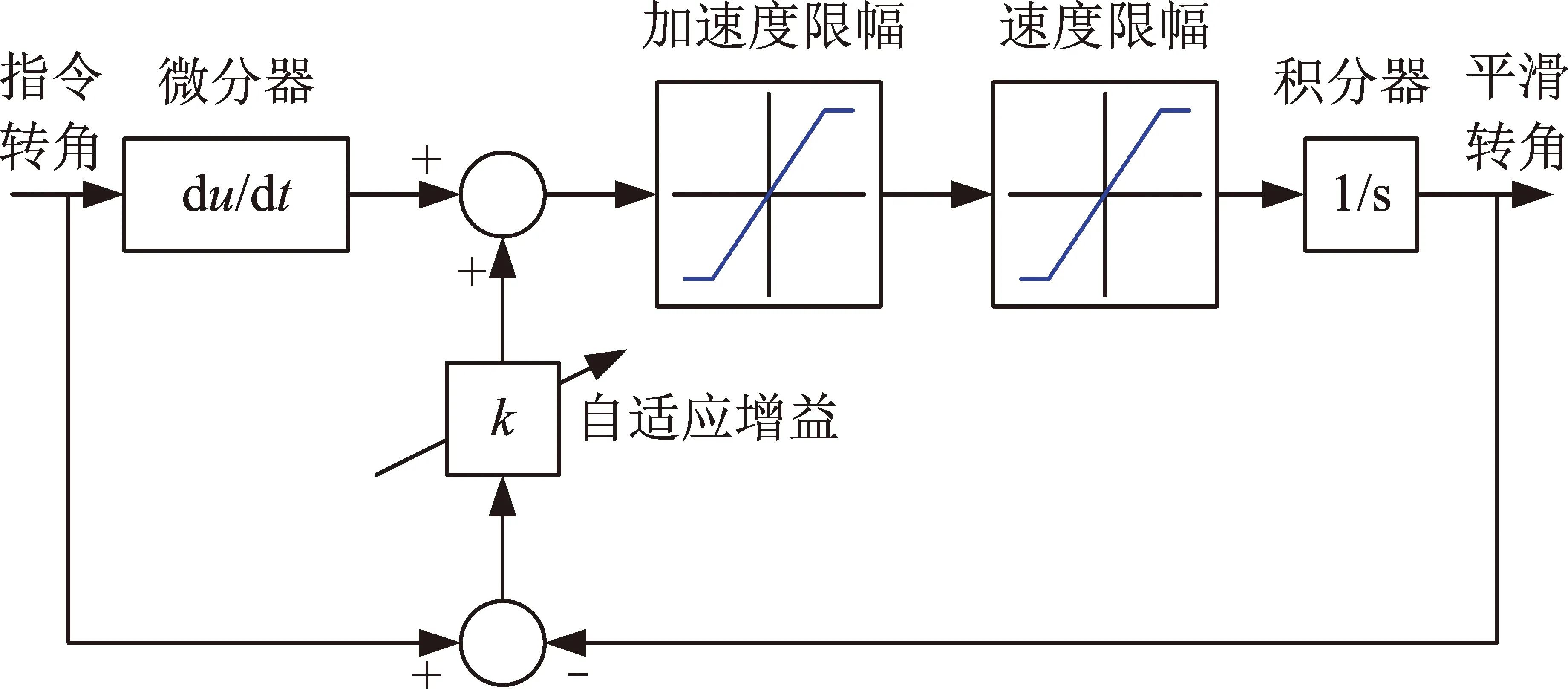
图3 天线转角轨迹平滑框图Fig.3 Block diagram forantenna rotation trajectory

自适应转角补偿控制参数计算：

kant,i=kant,0+kant,v·exp(-β|αr(t)-αp(t)|)

(7)

式中：αr(t)为当前周期根据目标计算的期望转角αr(t)，αp(t)为天线当前平滑后的实际转角指令αp(t)。高分七号选取自适应转角补偿控制器参数：kant,0=0.1，kant,v=0.2，β=10.0。

当前角速度为

(8)

期望转角指令更新为

αp(t)=αp(t)+Δt·(ωant,r(t)+kant,i·

(αr(t)-αp(t)))

(9)

4)数传天线的干扰力矩前馈补偿

高分七号卫星采用基于差分角动量的数传天线扰动补偿控制算法。假设控制计算机与天线系统的通讯间隔为Δt，可根据在一个通信间隔内天线转角指令计算出天线运动角动量变化量

ΔHa=Ha(t+Δt)-Ha(t)

(10)

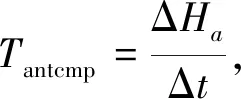
5)控制器设计

在正常对地定向姿态下，采用整星零动量的三轴轮控方式，设计了经典比例-积分-微分控制(PID)控制器，控制系统简化如图4所示。

图4 控制系统框图Fig.4 Block diagram for control system

为了得到更好的控制品质，提高抗干扰能力，在PID控制算的基础上引入天线干扰力矩的前馈补偿、磁力矩的前馈补偿和偏流角力矩的前馈补偿，可避免天线预置和跟踪时对星体稳定度的影响，避免磁力矩器在产生卸载力矩时对星体稳定度的影响，大大提高星体的稳定度。

2.4 侧摆机动控制

为了实现敏捷姿态机动，卫星控制分系统可采用双控制力矩陀螺(CMG)进行姿态控制[8]。高分七号卫星采用剪刀式安装构型，双CMG安装方式为两个CMG零位时角动量矢量相反，且角动量矢量方向与低速框架轴矢量方向均垂直于需要提供机动力矩的星体轴向。

基于剪刀式安装构型的双CMG力矩分配的基本原理，是根据期望的机动控制力矩在两个CMG之间进行合理分配，同时通过算法设计使两CMG框架角尽量保持同步，避免在其它方向产生扰动力矩。

如图5所示，机动轴为X轴，两CMG角动量在框架角零位时方向相反，均垂直于X轴，并在机动过程中相对于X轴对称，因此所提供的机动控制力矩沿X轴方向。定义期望的CMG控制力矩TCMG沿X轴正方向时为正，定义CMG1的框架角δ1为其角动量HCM1与X轴垂直时为零，向X轴正方向转动时为正。同理定义CMG2的框架角δ2为其角动量HCM2与X轴垂直时为零，向X轴正方向转动时为正。

图5 剪刀式安装构型双CMG示意图Fig.5 Block diagram for scissors configuration of two CMG

单个CMG低速框架转动提供的力矩为

(11)

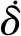
力矩方向垂直于框架轴和角动量矢量方向。随着框架角的转动，力矩方向将分为沿X轴方向与垂直于X轴方向。

CMG1产生的沿X轴方向和垂直于X轴方向的力矩分别为

(12)

CMG2产生的沿X轴方向和垂直于X轴方向的力矩分别为

(13)

以图5为例，垂直于X方向的力矩极性定义为向右为正，向左为负。因此当两个CMG的框架角度和角速率均相等时，将产生只有沿X轴方向的合成力矩。

根据PID控制率和前馈力矩综合计算出滚动轴的期望力矩TCMG，基于剪刀式安装构型的双CMG力矩分配算法计算出两个CMG的低速框架角速度指令。

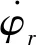
在满足卫星侧摆指标前提下，根据CMG的控制能力设计高分七号卫星侧摆时的加减速力矩和机动的最大角速度，由两个CMG同时工作提供绕滚动轴的控制力矩。

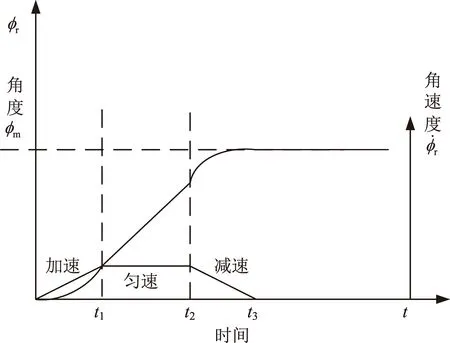
图6 侧摆轨迹示意图Fig.6 Sketch of maneuver trajectory planning of swayed attitude

3 在轨验证

3.1 相对安装误差标定算法验证

高分七号卫星采用相对安装误差的标定算法。在轨期间，前视相机一体化安装的星敏感器1a相对基准星敏感器的安装误差如图7所示。

图7 星敏感器相对安装偏差标定曲线Fig.7 Calibration result of opposite bias built in star sensors

从标定结果可知，以目前的技术水平，由于精测误差、入轨后的形变等因素，将引起星敏感器安装矩阵的变化，为提高定姿精度，有必要对安装误差进行标定补偿。由于星敏感器存在随机的测量误差，使得星敏感器相对安装偏差标定存在一定的波动，可通过滤波将该波动控制在角秒量级以下。

3.2 高稳定度SADA闭环控制验证

高分七号卫星入轨初期高稳定度SADA采取开环控制，过境时地面注入指令，引入高刚度高稳定度SADA的闭环控制。由图8的三轴卫星姿态角速度曲线可知，高稳定度SADA工作时卫星稳定度得到了大幅的提高。

图8 在轨姿态角速度曲线Fig.8 Estimated attituderate for three axes on orbit

3.3 天线轨迹平滑和干扰力矩补偿算法验证

高分七号卫星在轨数传天线在预置跟踪过程中对卫星稳定度的影响约为0.002 (°)/s，在轨指令引入数传天线轨迹平滑和干扰力矩补偿算法，引入后数传天线在预置跟踪过程中对卫星稳定度的影响大大减小，达到了预期效果。

图9给出了数传天线1进行预置跟踪时的天线指令转角和实际转角曲线，以及此时卫星的三轴姿态角速度曲线，由图10可以看出，引入数传天线在预置跟踪过程中的指令平滑和干扰力矩补偿后对卫星的三轴姿态角速度小于0.000 5 (°)/s。

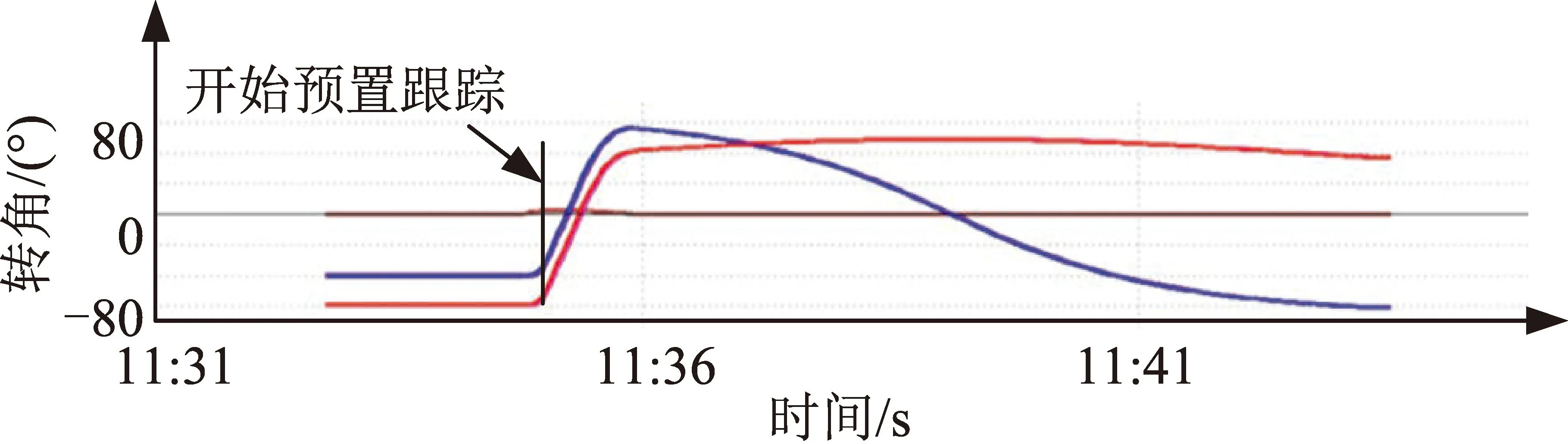
图9 天线平滑转角Fig.9 Antenna trajectory angle

图10 引入天线轨迹平滑和天线干扰力矩补偿后 的三轴姿态角速度Fig.10 Estimated attituderate for three axes after antenna trajectory smooth and disturb feedback

3.4 在轨运行结果

根据高分七号卫星的太阳翼基频和执行机构控制能力和系统指标要求，选取PID控制的控制带宽和阻尼比。卫星采用考虑轨道进动的轨道系相对于惯性系的角速度计算方法，由下图可知，卫星的稳定度得到了提高。

卫星在轨稳态运行时的姿态预估和角速度估计(含偏流角及偏流角角速度控制)曲线如图11所示。侧摆机动测试中的三轴姿态角曲线如图12所示。

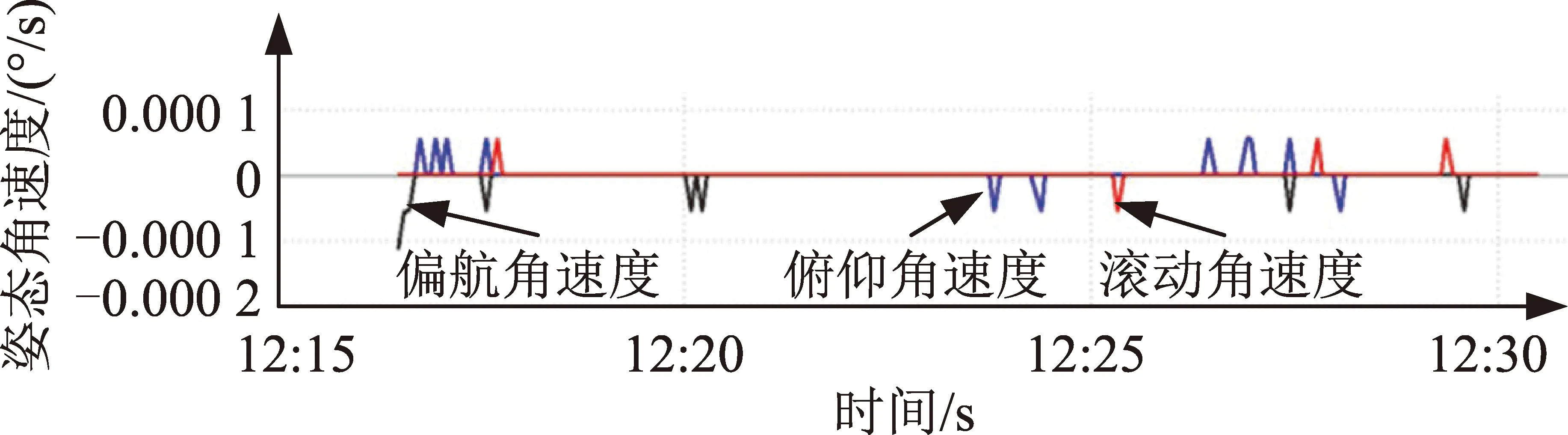
图11 三轴角速度曲线Fig.11 Estimated attitude rate for three axes

图12 侧摆过程中的三轴姿态角曲线Fig.12 Estimated attitude angles for three axes in swayed process

在轨数据表明，卫星可完成偏流角及角速度控制，扣除标称偏流角后，姿态控制误差优于0.005°，稳定度优于0.000 06(°)/s，为卫星实现高分辨率的立体测图提供了稳定运行平台。

4 结束语

本文介绍了高分七号卫星姿态控制分系统的姿态确定和姿态控制方案，在姿态确定上采用与前后视相机一体化安装的甚高精度星敏感器和相对安装偏差基准标定算法，选取高刚度高稳定度SADA进行太阳翼跟踪控制，在姿态控制上进行数传天线轨迹平滑和前馈力矩补偿，根据在轨运行结果表明，实现了优于0.000 06(°)/s的稳定度指标。高分七号的设计方案，可以供其他遥感卫星姿态控制分系统借鉴。