高稳晶振短期频率稳定度的仿真分析

贾丽娜 彭慧丽 于德江 杨 科

(北京无线电计量测试研究所，北京 100039)

1 引 言

高稳晶振以其优异的短稳性能在科学研究中得到越来越多的应用, 对其短期频率稳定度的研究也越来越深入。高稳晶振在工作中, 输出频率受到多种因素的影响, 频率稳定度受到不同程度的恶化。分析研究各个扰动因素及其对稳定度恶化的影响特性, 是高稳晶振研究中提高稳定度的必要途径[1]。

针对晶振老化和温度特性对频率稳定度的影响，研究了不同条件下高稳晶振短期频率稳定度的仿真分析方法。在对时域频率稳定度进行分析的基础上，建立短期频率稳定度仿真分析模型，并结合工程实际引入了晶振老化特性和温度特性对频率稳定度影响的数学模型。利用此模型，对不同老化条件和温度条件下高稳晶振的短期频率稳定度进行了分析计算，仿真分析结果与晶振实测结果较为一致，可为高稳晶体振荡器设计提供指导。

2 时域频率稳定度分析方法

频率稳定度表征方法分为时域和频域两种[2]。频域上通常采用单边带相位噪声描述频率稳定度，时域上则给出了不同方差来描述，其中阿伦方差应用最为广泛。

2.1 频率源信号数学模

频率源的输出信号一般为正弦波信号，可以将此信号表示为

V(t)=[V0+ε(t)]sin[2πf0t+φ(t)]

(1)

式中：V0,f0——标称振幅和频率；ε(t),φ(t)——振幅起伏、相位起伏；t——时间。

分析频率源的稳定度时，主要考虑相位起伏φ(t)的影响。相对频率偏差可以表示为

(2)

其中，

(3)

式中：y(t)——振荡器相对频率偏差，表征了振荡器的频率稳定度；x(t)——振荡器瞬时相位变化所引起相对于参考系理想时间的差，表征了频率源的时间稳定度。

时域中频率稳定度的分析，可以通过对y(t)和x(t)的处理来进行。

2.2 稳定度计算方法

幂律噪声谱模型是Lesson给出的经典振荡器噪声模型，它认为相位噪声是由五种独立的噪声组成，即随即游走调频噪声、闪变调频噪声、白色调频噪声、闪变调相噪声和白色调相噪声[3]。其中几种噪声并非平稳随机过程，这使得用标准方差描述频率稳定度时，计算结果会随着平滑时间的加长而发散，与真实方差偏离。基于以上原因，阿伦方差，哈达玛方差，总方差等表征方式发展起来，在频率稳定度领域逐渐成为主流的表征方式[4]。

对频率稳定度的计算主要采用重叠阿伦方差，其计算公式为[5]

(4)

式中：N——数据点的总数；m——对应平滑时间的乘数；τ0——数据采样间隔，即τ=mτ0。

3 短期频率稳定度分析模型构建

基于对频率稳定度计算过程的分析，利用Matlab作为仿真平台，构建了短期频率稳定度的分析模型。同时为了在后期分析数据时更加便捷，直观，易于操作，借助Matlab提供的图形用户界面(GUI)功能[6]，设计了频率稳定度分析系统，系统的分析流程如图1所示。

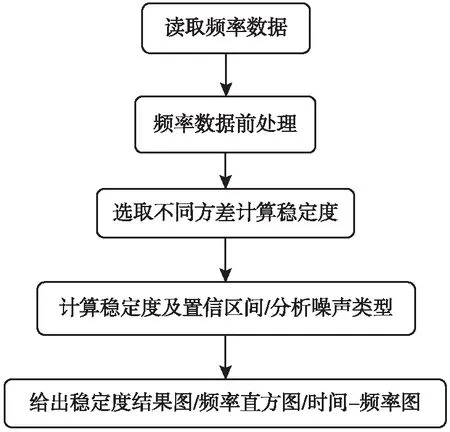
图1 稳定度分析流程框图

(5)

式中：yi——频率相对起伏；f0——标称频率；ti——取样时间；τ——取样间隔；φ——相位值。

在对频率数据进行前处理去掉偏移以及离群值之后，为了稳定度分析计算更加方便，速度更快，将频率数据转换为相位数据。设读取的离散频率数据为freqdata，其标称频率为reffreq，计算相对频率偏差为y=(freqdata-reffreq)/reffreq，根据频率与相位之间的关系可以得到

(6)

式中：x——相位数据。

对于离散采样得到的频率数据，有y[i]=(x[i+1]-x[i])/τ。因此，可以推导相位数据为

x[1]=0

x[2]=y[1]

x[3]=y[2]+y[1]

x[4]=y[3]+y[2]+y[1]

………

x[i]=y[i-1]+x[i-1]

(7)

逐个递归之后，x乘以采样间隔，即x·τ0，得到可以直接代入式(4)中进行稳定度计算的相位数据x。

本仿真分析模型基于LAG1自相关法[5]得到不同平滑时间点的噪声类型。根据如图2所示的不同噪声类型与其系数对应关系能够得到噪声识别区间，见表1。计算噪声系数可以得到相应平滑时间点的主要噪声类型。

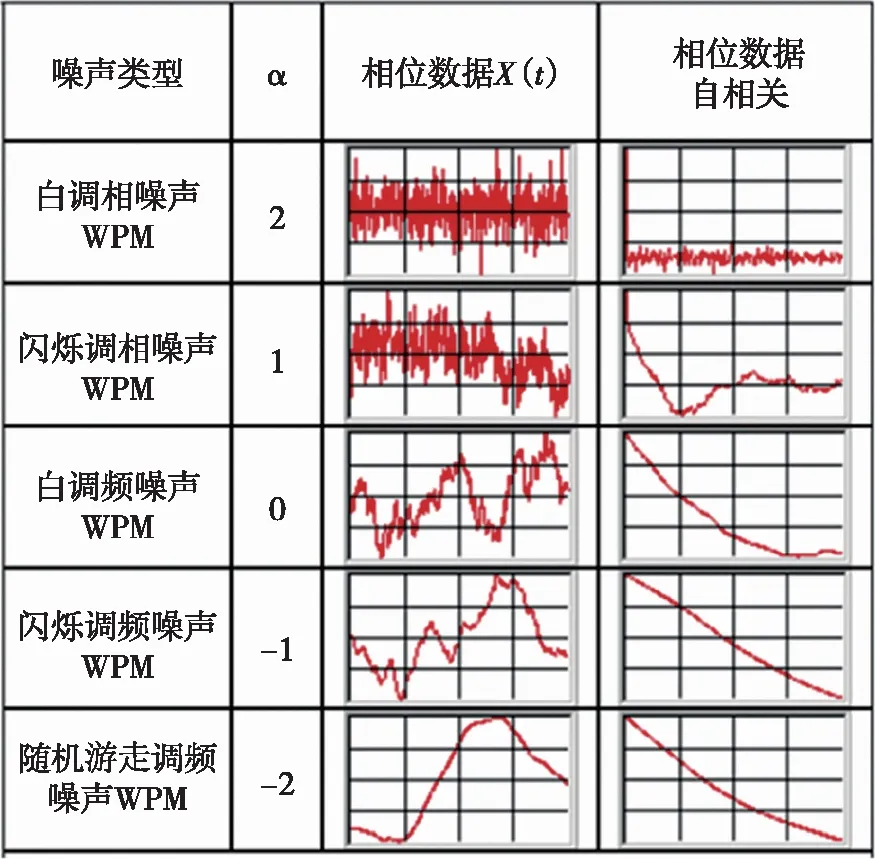
图2 不同噪声类型相位数据示意图

对10MHz高稳晶振实测频率数据利用此分析模型选择重叠阿伦方差计算频率稳定度，分析结果如图3所示，与实际短稳分析仪给出的结果一致，能够验证此分析模型的有效性。

表1 幂律噪声类型识别区间Tab.1 Power law noise type identification interval噪声类型幂律噪声系数α识别区间WPM2α≥1.5FPM11.5>α≥0.5WFM00.5>α≥-0.5FFM-1-0.5>α≥-1.5RWFM-2-1.5>α≥-2.5FWFM-3α≤-2.5

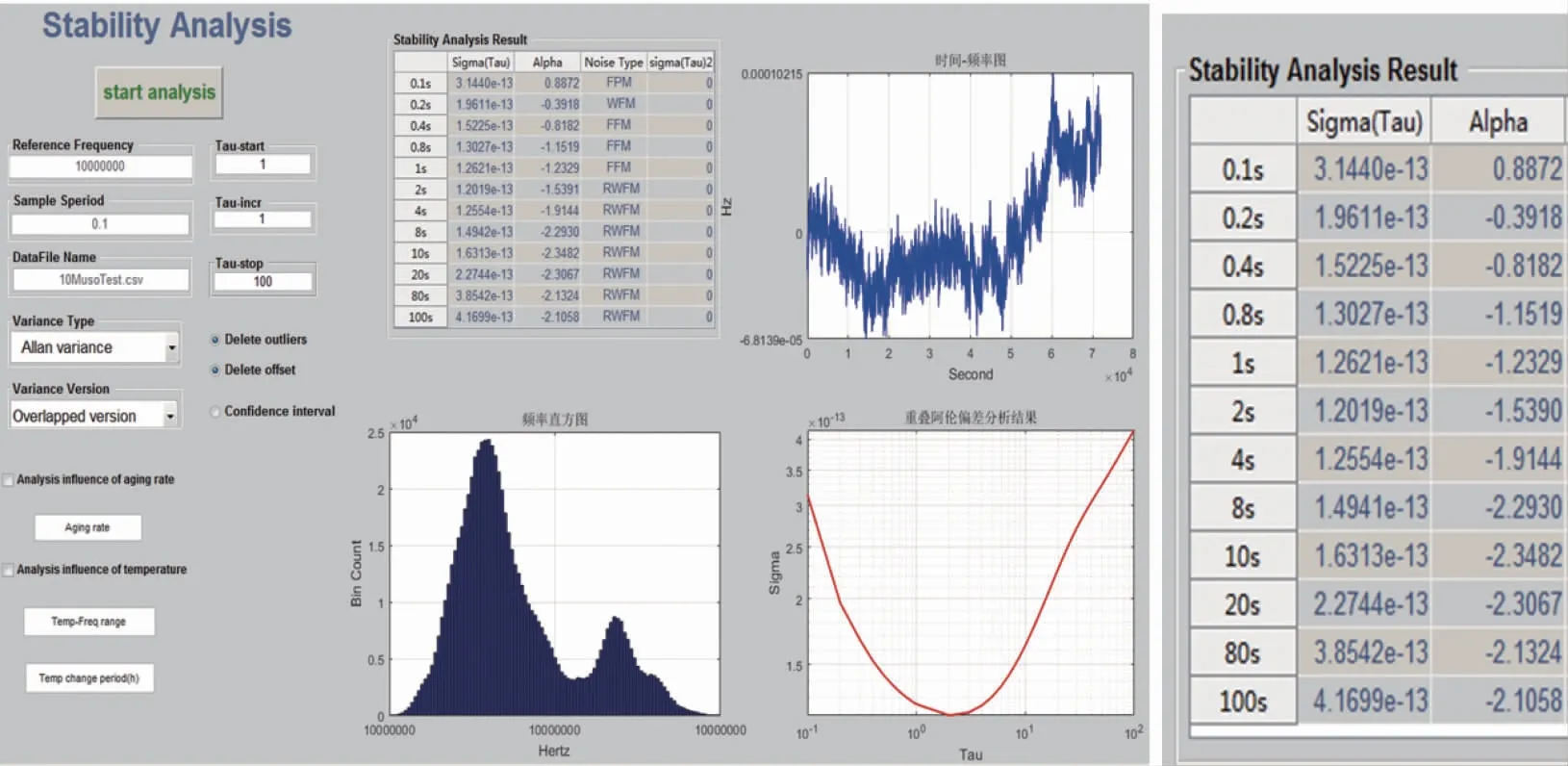
图3 实测晶振数据稳定度分析结果示意图

4 老化及温度特性对晶振稳定度的影响分析

影响晶体振荡器输出频率稳定度的因素有多种，如电路噪声、老化、温度、振动、辐射等。基于高稳定度晶体振荡器的设计，从晶振老化特性以及温度特性两方面进行研究，建立其对短期频率稳定度影响的数学模型，对不同条件下的短期频率稳定度进行定量分析和计算。

采用随机生成的方法得到一组可以模拟晶振输出的频率数据，此数据长度为720 000，采样周期设置为0.1s，可以模拟晶振在20h内的连续输出频率读数。在不加任何影响的情况下从如图4所示的频率数据波动在标称频率附近，呈正态分布，稳定度曲线符合实际，认为其能够模拟只含电路噪声情况下的晶振输出频率。

图4 模拟晶振输出频率数据的分析结果示意图

4.1 晶体谐振器老化特性对晶振稳定度影响的分析

晶体的老化特性会引起晶振输出频率的缓慢漂移[3]。从晶体初始接入电路起，其老化曲线呈现对数形式，即前期晶体老化造成频率漂移幅度较大，而后期逐渐趋于平缓。这种老化过程一般对晶振长期频率稳定度影响较大，但当测试时间持续较长时，老化特性也会影响短期频率稳定度。

分析晶振老化特性对稳定度的影响可以通过建立简化数学模型实现。假设经过老化处理后晶振的老化曲线是一条斜率很小的直线，此斜率即老化率。

取日老化率为agingrate=(f-f0)/f0，对频率数据重新赋值，叠加老化特性的影响为

freqdata(i)=freqdata(i)+agingrate×f0

×τ0×i/86400

(8)

式中：freqdata——频率数据；agingrate——日老化率。

式(8)得到的数据即为加上老化特性的晶振输出频率。当叠加的日老化率分别为1E-11、5E-11、1E-10、5E-10时，频率随时间的变化如图5所示，其稳定度分析结果如图6所示。

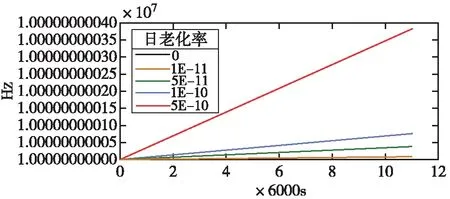
图5 6000s不同老化率下时间-频率图

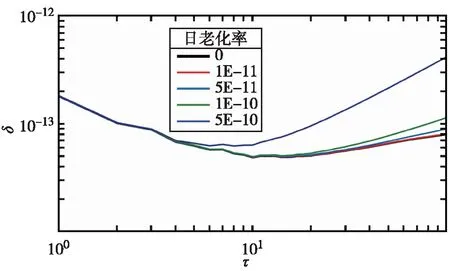
图6 不同老化率下稳定度分析结果图

由图6可知，老化特性对晶振稳定度的影响随着平滑时间变长而加大。当平滑时间为(1～10)s时，日老化率在5E-10到1E-11的范围内，对晶振稳定度基本没有影响，其稳定度均在2E-13以内。而当平滑时间为(10～100)s时，日老化率越大，对频率稳定度的影响也越大。如日老化率为5E-10时，频率数据稳定度分析结果与图4中的原始值相比，出现了较大偏离，10s稳定度从4.94E-14变为6.42E-14、100s稳定度从8.07E-14变为4.17E-13；日老化率为1E-10时，100s稳定度的整体变化幅度小于3.2E-14；日老化率小于5E-11时，稳定度分析结果基本没有变化，接近图4中的原始值。

4.2 晶体振荡器温度特性对稳定度的影响分析

对于晶振而言，温度是影响晶振输出频率稳定度至关重要的一个因素[7]。在恒温槽及控温电路的精密设计下，晶振的频率温度稳定度能够实现在宽温度范围内小于1E-9[8]。但是，由于控温电路与恒温槽结构对于环境温度变化的响应速度和内部控温特性不同，导致晶振输出频率总是会叠加由于温度特性引起的周期性波动。因此，本文讨论了晶体振荡器温度特性对稳定度的影响。

结合晶振温频曲线特征，将上述周期性波动建模为正弦曲线。设温度特性导致频率相对变化幅度为TR，周期为T(单位s)，对原始频率freqdata，重新赋值为

freqdata(i)=freqdata(i)+|TR|

(9)

得到的数据即为叠加了晶振温度特性对输出频率影响的数据。对此读数进行稳定度分析，可以观察频率波动周期以及幅度对晶振短期频率稳定度的影响。

设定频率波动为5E-11，原始数据与波动周期分别为300s，900s的时间-频率图如图7所示。

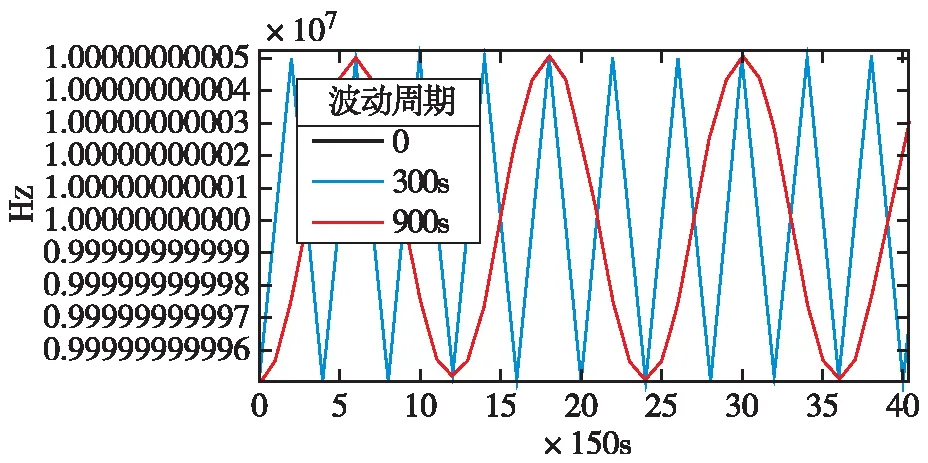
图7 频率波动幅度5E-11时，不同波动周期下时间频率图

波动幅度分别设置为1E-12，8E-13，3E-13时，不同波动周期下稳定度分析结果如图8至图10所示。由图8-图10可知，施加温度特性的影响后，对晶振(1～100)s稳定度都造成了不同程度的恶化。

图8 频率波动幅度分别1E-12时，不同波动周期下稳定度分析结果图

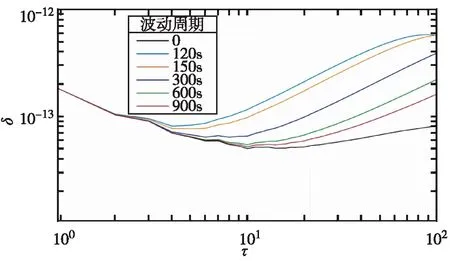
图9 频率波动幅度分别8E-13时，不同波动周期下稳定度分析结果图

图10 频率波动幅度分别3E-13时，不同波动周期下稳定度分析结果图

当固定频率波动周期时，频率波动幅度越大，对稳定度的影响越大。当固定频率波动幅度时，频率波动周期越小，对短稳的影响越大；且平滑时间越长，由温度特性带来的影响越大。例如波动幅度为1E-12、波动周期为120s时，10s稳定度就已经相比原始数据恶化6E-14。而当波动周期为900s时，100s稳定度相比原始数据恶化程度仅有3E-14。

4.3 实测数据分析

采用科尔皮斯电路，SC切三次泛音晶体设计并制作了10MHz高稳晶体振荡器，不同频率漂移下的稳定度实测结果，如图11和图12所示。能够看到，

图11 实测晶振率漂移8.75E-12/h，稳定度分析结果图

图12 实测晶振4h频率漂移1.25E-12/h，稳定度分析结果图

当晶振输出频率漂移为8.75E-12/h，测得的短期频率稳定度分析结果为7.4E-13@10s，1E-12@100s。当晶振输出频率漂移为1.25E-12/h，测得的短期频率稳定度分析结果为2.5E-13@10s，4.4E-13@100s，实现高稳定度，与本章中分析模型给出的结论一致。

4.4 短期频率稳定度仿真分析

根据仿真分析结果，晶振老化特性和温度特性对晶振短期频率稳定度都会产生不同程度的影响。

晶振老化特性对频率稳定度的影响随着平滑时间的加长而增大，且日老化率越大，晶振短期频率稳定度恶化得越多。欲设计平滑时间为(1～100)s，短期频率稳定度小于2E-13的高稳定度晶体振荡器，所采用的晶体谐振器的日老化率需小于5E-11。

晶振温度特性对频率稳定度的影响与频率波动周期和波动幅度相关。频率波动周期一定时，波动幅度越大，晶振短期频率稳定度恶化得越多；波动幅度一定时，波动周期越短，短期频率稳定度恶化得越多。当频率波动幅度小于3E-13，波动周期在(120～900)s时，对晶振频率稳定度的影响基本可以忽略，满足(1～100)s短期频率稳定度小于2E-13的高稳晶振的设计要求。

本文给出的分析模型和仿真方法，能够结合实际测试，在分析控温设计数学模型的基础上，定量给出分析结果，相比以往的经验推导，更具指导意义。

5 结束语

本文深入研究了频率源输出频率稳定度的理论基础，基于Matlab设计了短期频率稳定度分析程序。通过对比同组数据的计算和实测结果，验证了分析程序计算结果的可信度。结合工程实际，考虑晶体老化特性与温频特性对晶振稳定度的影响，建立了简化数学模型，进行不同条件下稳定度的仿真分析。实际设计制作了高稳晶振，其稳定度测试结果与仿真结果较为一致，证明仿真分析的有效性。本文提出的仿真分析方法相较以往的经验推导，可以给出更为准确直观的数字结果，以帮助深入分析晶振产品设计过程中各种因素对频率稳定度的影响，加速推动高稳晶振产品的实现。