高分七号卫星载荷任务管理中的解耦设计

张莎莎 莫凡 丁建钊 徐文强 姚鑫雨 刘付强

(1 北京空间飞行器总体设计部，北京 100094)(2 北京控制工程研究所，北京 100094) (3 西安空间无线电技术研究所，西安 710071)

随着近地遥感卫星技术的发展，卫星载荷数量和功能也不断提升，就使得工作模式设计较为复杂。因此为方便卫星用户使用，遥感卫星普遍开展了星上自主任务管理设计。

国外在卫星自主任务规划和管理方面已相继开展了相关的技术研究。NASA在地球观测(EO-1)卫星的基础上，先后开发了自主调度与规划(ASPEN)[1]及调度和执行程序框架(CASPER)[2]两大卫星任务规划系统。ESA支持的星上自主计划(PROBA)[3]研究并验证了一些星载自主规划技术；法国国家空间研究中心(CNES)在其昂宿星(Pleiades)上开展了卫星自主任务规划系统的试验[4]。与此同时，国内也开展了很多遥感卫星任务规划技术研究。贺仁杰等人针对地面多星任务规划问题提出了规划模型和算法，并开发了一整套地面任务规划系统，但该系统目前主要应用于地面[5]。田志新等人提出基于有向图模型的卫星任务指令生成算法，首次在星上实现任务级指令到执行级指令的分解，该方法中虽然统筹考虑了观测任务和回放任务，但对于观测和回放任务的解耦工作仍由地面系统而非卫星自主完成[6]。

高分七号(GF-7)卫星是一颗高精度民用测绘卫星，卫星轨道高度约500 km，星上装载了前、后视测绘相机和激光测高仪，通过对同一区域不同角度的观测，实现1∶10 000比例尺卫星测绘。本文分析了GF-7卫星工作模式的特点，以典型的观测模式和回放模式为设计基础，梳理了两种工作模式间的约束和耦合关系，并从消除耦合、简化卫星任务管理、提升卫星对任务的快速、无条件响应的需求出发，提出了一种适用于星上自主任务管理的工作模式解偶设计，有效满足了不同工作模式的无约束实现。

1 卫星工作模式解耦设计的必要性

1.1 卫星工作模式简介

GF-7卫星对地观测任务的完成包括观测记录和数据回放两个活动。

观测记录模式(简称观测模式)，由地面观测目标触发：卫星飞经观测目标时，卫星平台将飞行姿态调整至观测所需姿态，有效载荷开机并对地观测，星上数据处理及传输系统对载荷观测数据进行处理、格式编排后，实时送入星载存储器进行存储。当进行连续多目标成像观测时，则卫星平台需在多个目标的间隔时间内完成快速姿态机动和稳定，以使得载荷观测视场指向各观测目标。

数据回放模式(简称回放模式)由地面站可视条件触发：卫星飞经地面站可视范围内，星上数据处理及传输系统对载荷观测数据进行回放。为提高卫星对地回放时的等效全向辐射功率(EIRP)，卫星采用X-Y二维机械转动的高增益点波束天线，在对地面站传输过程中，需实时控制X、Y轴转动，使得天线波束中心始终指向地面站。

1.2 卫星工作模式间的耦合因素分析

除1.1节所述的触发条件之外，卫星工作模式还分别与图1所示的各因素有关。

从图1的梳理中可以看出，卫星观测模式和回放模式的耦合因素为卫星平台姿态：一方面，观测模式提出对卫星姿态的期望，卫星控制系统根据该期望，依照一定的控制策略，控制偏航、俯仰和滚动轴转动来执行姿态调整；另一方面，平台姿态是回放模式中天线对地面站指向角度的决定因素之一。由此，产生两种任务之间的耦合关系，如图2所示，即观测任务决定卫星姿态，卫星姿态决定回放任务中天线指向。

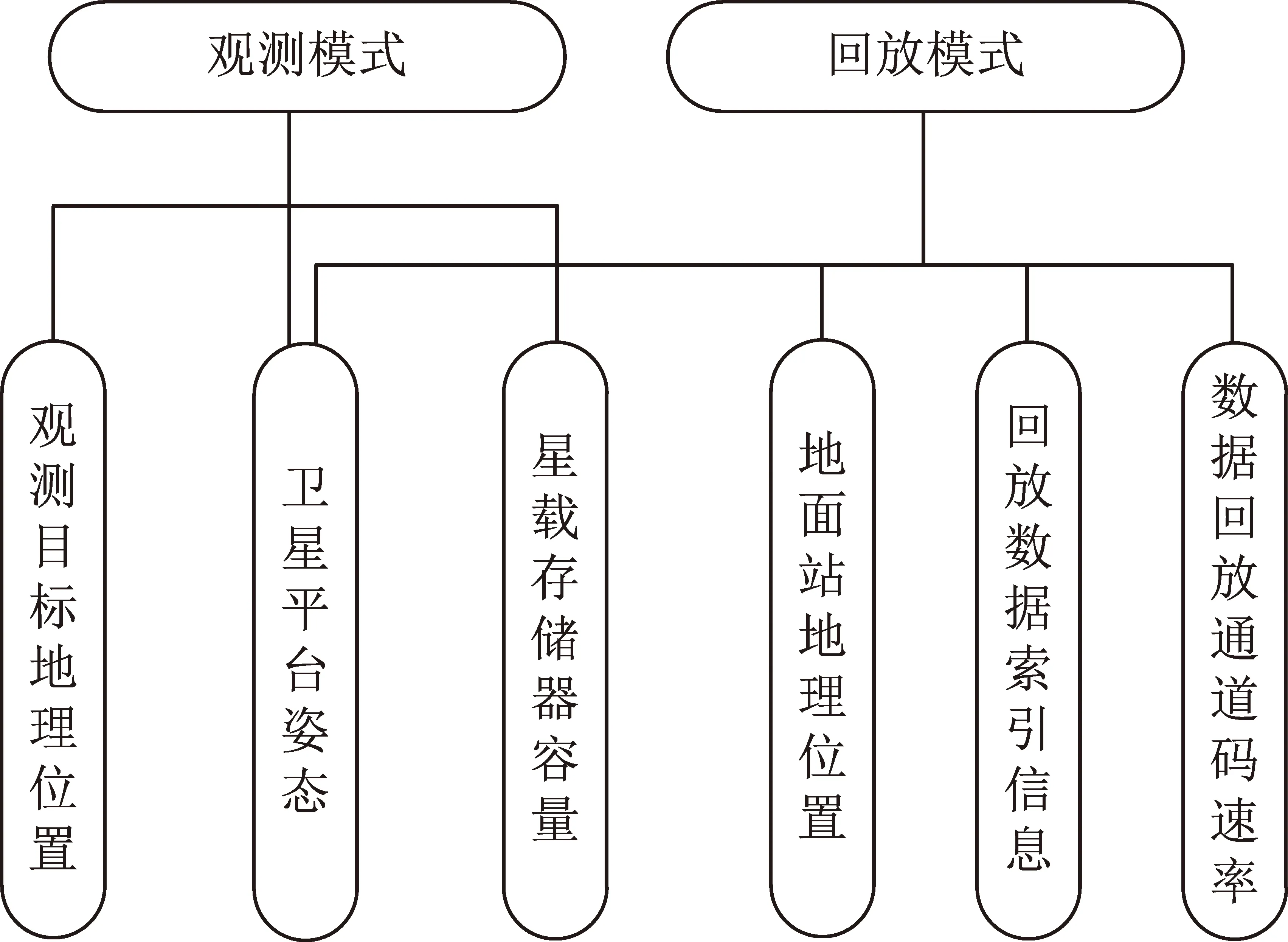
图1 遥感卫星工作模式耦合因素Fig.1 Coupling factors of working modes of a remote sensing satellite

图2 卫星姿态对观测记录模式和数据 回放模式的耦合关系Fig.2 Coupling relationship between observation recording mode and data playback mode in terms of satellite attitude

1.3 解耦设计必要性分析

为提高用户使用体验，使得卫星能够在满足各模式触发条件的基础上即可制定和执行相应的模式，GF-7卫星提出观测模式和回放模式可并行执行、互无影响的使用需求。但由于在观测模式准备过程中，为达到其期望姿态，需要进行三轴姿态机动，机动过程为：初始姿态角度→匀角加速度α加速至最大角速度ω→以角速度ω做匀速转动→匀角加速度减速至0(°)/s→机动到位。对于连续点目标观测模式来说，需要卫星在两个点目标之间完成敏捷姿态机动；而传统的回放模式设计均是以固定姿态角度为输入，进行天线对地面站指向角的计算，未考虑姿态机动过程中由于姿态角的持续变化带来的天线对地面站指向角的变化，这样就会导致天线指向角度误差随着控制周期的增加而持续累加，最终超出±0.5°的指向精度要求，从而无法满足敏捷机动点目标观测过程中的数据回放。

综上，为满足卫星观测模式和回放模式的无干扰并行执行，就必需进行针对卫星姿态的解耦设计，在回放模式执行过程中，将卫星姿态预报引入天线指向角计算，以此提高天线指向精度。从而使得观测模式和回放模式均能按照各自的触发条件进入并执行，相互之间无干扰、无制约。

2 低轨遥感卫星工作模式解耦设计

2.1 卫星姿态测量及转换

要进行卫星姿态预报，首先需要进行当前及历史姿态的测量。卫星姿态一般指卫星本体相对于轨道坐标系下零姿态的偏差。GF-7卫星配置星敏感器完成姿态高精度测量。在姿态测量及转换过程中，涉及到以下坐标系及转换关系：①星敏感器完成从星敏感器坐标系到惯性空间坐标系(J2000系)的转换矩阵的实时测量，记为Tis；②设卫星从惯性坐标系到轨道坐标系的转换矩阵为Toi通常通过星载导航接收机或地面轨道测量数据计算得到；③设卫星从轨道坐标系到本体坐标系转换矩阵为Tbo；④设卫星从星敏感器坐标系到本体坐标系的转换矩阵Tbs，通常通过地面标定得到。

上述几个转换矩阵具有如下关系

Tbs=Tbo×Toi×Tis

(1)

进而可得

Tbo=Tbs×(Tis)T×(Toi)T

(2)

式(2)中，Tis通过星敏感器测量并计算得到。通常，星敏感器的输出采用四元数Q的形式，有

Q=q0+q1i1+q2i2+q3i2

(3)

式中：q0表示四元数的标量部分，q1、q2、q3表示四元数的矢量部分，则有

(4)

若卫星选用Z→Y→X转序，则对应欧拉角表示的姿态矩阵为

(5)

式中：α、β、γ分别表示卫星星体沿X、Y、Z三个轴向的姿态角。由此可得

(6)

式中：Tbomn表示坐标系转换矩阵Tbo中的第m行第n列的元素。

2.2 卫星姿态预报方法

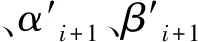
2.3 工作模式解耦算法流程

采用二阶多项式拟合的姿态预报及解耦算法流程如下：

(1)利用星敏感器输出的q值，计算得到当前时刻卫星本体坐标系相对于轨道坐标系的欧拉角，即得到卫星三轴姿态角；

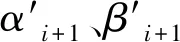
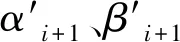
3 验证与分析

为了验证姿态预报算法的正确性和精度，采用GF-7卫星轨道作为算例，利用本文研究的姿态预报算法，结合数传天线对地面站指向角度的预报，并利用卫星实际执行的姿态进行验证，最终得到由于姿态预报误差引起的天线指向角度误差。

3.1 算例说明

1)轨道信息

算例的卫星轨道参数见表1。

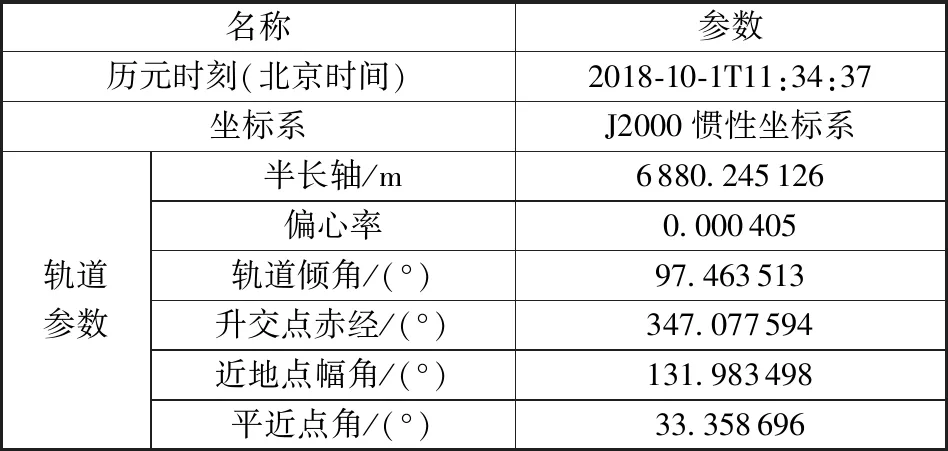
表1 算例的起始历元时刻轨道根数Table 1 Orbital elements at the beginning epoch time

2)地面站地理信息

算例中选用新疆喀什地区作为数传接收地面站，喀什站的地理位置信息由STK软件中自带的数据信息获得，地面站的约束条件为地面站仰角不小于5°，具体地理位置信息见表2。

在STK软件中将卫星起始历元时刻的瞬根参数作为卫星初始轨道参数值，采用HPOP模型，重力场模型选用21阶的WGS84_EGM96模型，STK软件的精确值中考虑了大气阻力，设定面质比为0.008 m2/kg，F10.7=150，并考虑了太阳光压和日月的三体引力影响。

表3为卫星过喀什地区地面站的时间。

表2 仿真用喀什站地理位置信息Table 2 Geographic location information of Kashi station for simulation

表3 卫星过喀站的时间Table 3 Arc segment of Kashi station

3)姿态机动情况

算例中，在卫星过喀地面站期间，进行姿态机动，具体为俯仰轴和偏航轴角度保持不变，滚动轴由0°变化至32°，且其机动过程中的姿态角加速度绝对值|α|=0.033(°)/s2，最大转动角速度ω=0.5(°)/s。具体的机动姿态角度曲线见图3。

图3 算例用姿态机动过程三轴角度曲线Fig.3 Three-axes attitude angle curves

3.2 结果分析

算例中利用本文的姿态预报算法周期性预报卫星在姿态机动期间的姿态角度，预报周期为0.5 s，拟合样本数为3，将预报得到的姿态曲线，以角度变化最大的滚动轴为例，与实际控制到位的姿态曲线进行比较，预报误差见图4。同时将姿态预报结果利用STK软件对预报姿态下的天线指向角度进行仿真，得到该状态下的指向角误差如图5和图6所示。

仿真分析结果表明：①该姿态预报算法引起的姿态角预报误差幅值范围为[-0.051°,0.053°]，该误差最大值出现在机动轴开始加、减速的时刻，而在匀速转动过程中，预报误差不超过[-0.02°,0.02°];②由姿态预报误差引起的天线X、Y轴指向角度计算误差幅值范围分别为[-0.055,0.040]和[-0.037,0.023]，该误差范围与姿态预报误差量级相当，对于指向精度优于0.5°的指标要求，该误差项贡献约为10%，可满足在轨使用。

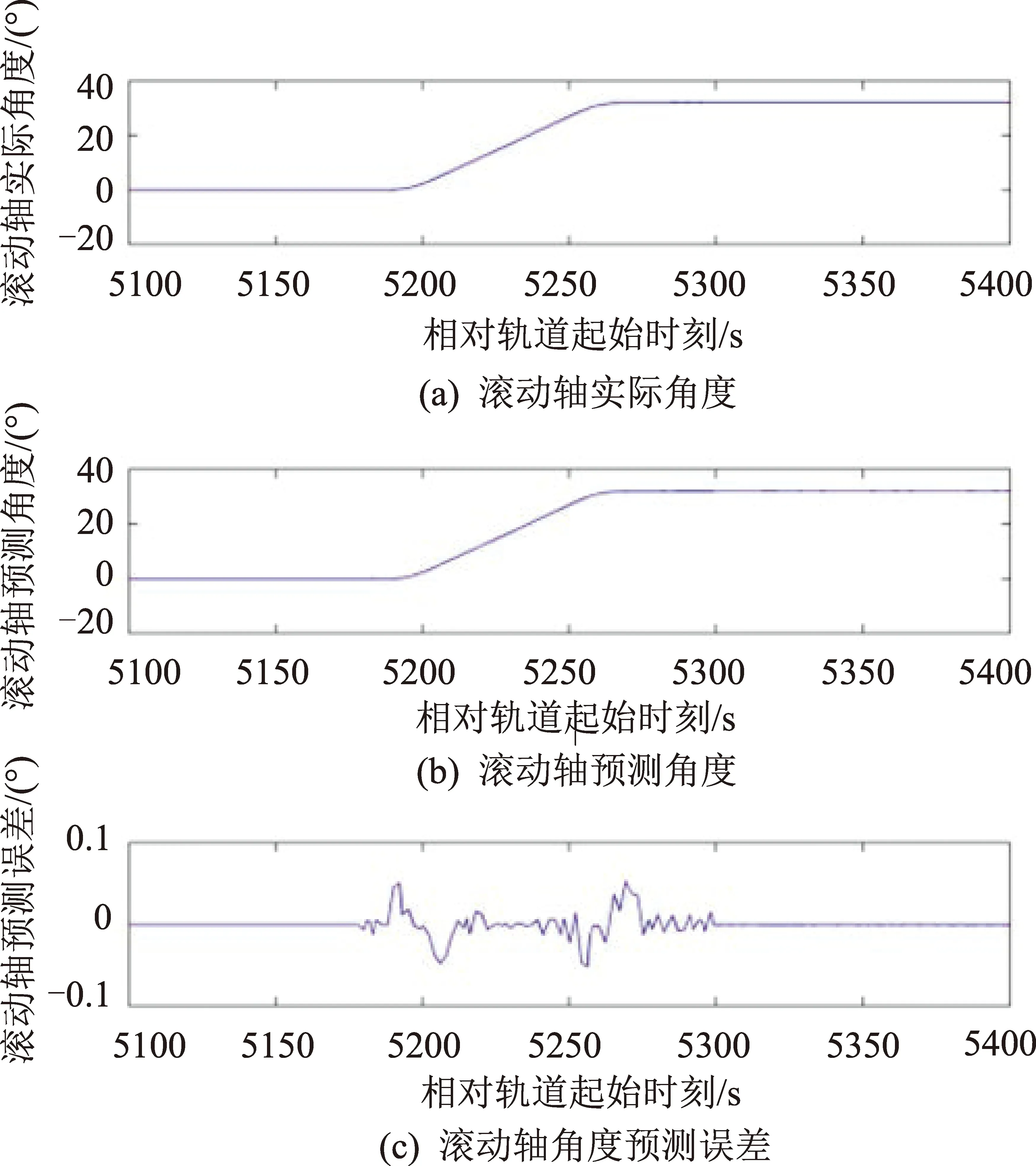
图4 算例输出的滚动轴姿态预报误差Fig.4 Predicted attitude angle error of rolling axis

图5 由姿态预报误差引起的天线X轴 指向角误差Fig.5 Pointing angle error of X-axis induced by attitude prediction error

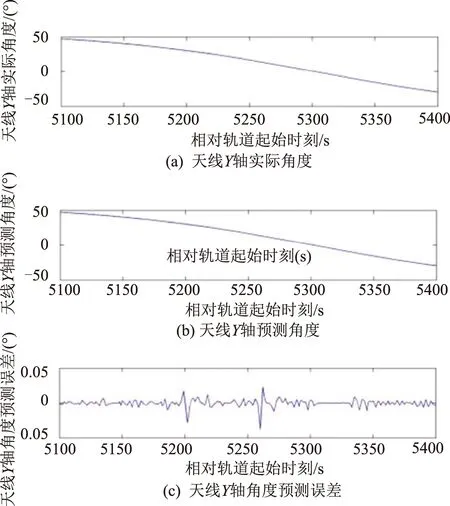
图6 由姿态预报误差引起的天线Y轴 指向角误差Fig.6 Pointing angle error of Y-axis induced by attitude prediction error

4 结束语

本文对低轨道遥感卫星观测模式、回放模式中的姿态耦合因素进行了分析，建立了解耦用的姿态预报模型。这种方法简单、易于星上实现，且预报精度可保证天线指向精度的工程要求，可作为星上工作模式自主运行使用。