应用简单时间网络的遥感卫星工作模式设计方法

任放 杜朝 陈曦 潘莉

(北京空间飞行器总体设计部，北京 100094)

遥感卫星工作模式设计是遥感卫星总体设计的核心内容。一般来说，遥感卫星有效载荷任务的完成包括成像和数据传输两项。在进行成像和数据传输过程中，遥感卫星典型工作状态为：①成像记录模式。卫星飞经感兴趣目标区域范围内，在处于正常飞行姿态或侧视飞行姿态并稳定一段时间后，有效载荷开机并对地成像，星上数据处理及传输系统对有效载荷观测数据进行实时处理、格式编排后，将处理结果送到星载数据存储器存储，等待卫星飞经地球站可视范围内时择机传输。②成像实传模式。卫星飞经地球站可视范围内(5°仰角以上为可见)，在处于正常飞行姿态或侧视飞行(卫星绕机动轴摆动一定角度)姿态并稳定一段时间后，有效载荷开机并对地成像，星上数据处理及传输系统对有效载荷观测数据进行实时处理、格式编排、信道编码、调制、放大、滤波后，将处理结果经数传天线发送至地球站。③数据回放模式。卫星飞经地球站可视范围内，处于正常飞行姿态时，星载数据存储器进行数据回放，数据经信道编码等处理后送至数传射频通道进行调制、放大、滤波，最后由数传天线发送至地球站[1]。

传统的遥感卫星工作模式设计大多采用人工手动设计方式，主要是通过对卫星用户的需求进行分析，并结合卫星设计状态，明确卫星在轨运行阶段主要工作状态及设备间协调工作的方式。在卫星系统较简单、有效载荷使用较单一的情况下，工作模式设计结果一般在几十种。随着任务复杂度、有效载荷应用的灵活程度提升，在轨所需的工作模式数量增长趋势明显，已经达到了上百种。因此，人工手动设计方法无法高效、准确完成卫星工作模式设计工作。简单时间网络(STN)是一种应用广泛的时间表示模型，具有表达能力强、计算方便等优点，便于时间管理，已被广泛应用于规划与调度领域[2]。国内方面，文献[3]中研究了STN表达时间冲突、资源冲突的方法，并提出冲突检测与消解方案；文献[4]中将STN应用于作战流程资源冲突的检测和消解；文献[5]中提出利用STN方法解决敏捷卫星调度的时间约束推理方法。国外也开展了很多基于STN方法的业务流程和规划时间研究[6]。文献[7]中提出STN中约束之间的动态平衡方法；文献[8]中提出STN从全局考虑以代价最小的方式解决冲突，其特点是通过冲突检测确保计划在相关时序约束下顺利完成。上述文献的研究成果表明，STN方法可有效用于解决时间冲突问题，但现有研究成果未针对卫星内多系统之间协同工作场景下的时间冲突给出解决方案。

本文提出一种应用STN进行遥感卫星工作模式时序设计的方法。对卫星工作模式进行动作分解，利用STN图形表示不同约束条件，并通过检测是否存在时序冲突以验证设计的正确性。高分七号卫星的应用结果表明：本文方法适用于复杂遥感卫星的工作模式设计，可应用于同类型遥感卫星工作模式设计中。

1 应用STN的工作模式设计方法

1.1 STN相关概念

在利用图形表达时间网络之前，更直观的方法是利用不等式组进行第一步约束的建立。简单时间问题(STP)是一个特殊的约束满足问题，它可表示为一个二元组其中，变量集X={X1,X2,…,Xn}代表事件的发生时刻(n为有约束关系的事件数量)，约束集C由一组形如an≤Xi≤bn或an≤Xj-Xi≤bn的约束不等式构成(i，j为有约束关系的事件编号，在本文中即为任务编号)，代表事件之间的时间约束关系。STP的求解是寻找一组能满足所有约束的值X={X1=a1,X2=a2,…,Xn=an}。当STP存在解时，称其是一致的，反之，称其为不一致。

可见，求解STP的本质就是求解一组形如an≤Xj-Xi≤bn的约束不等式。这种二元约束不等式比较特殊，其系数有一个为1，另一个为-1，称为差分约束。一般把差分约束不等式转化为图的形式，利用图算法来判断其一致性和求解。具体转化方法为：将时间变量X={X1,X2,…,Xn}表示为图中的点，将约束an≤Xj-Xi≤bn表示为一条弧Xj→Xi，其权重用区间[an，bn]标记。这样，STP就转化为一个特殊的加权有向图STN。

如图1所示，进一步把an≤Xj-Xi≤bn转化为Xj-Xi≤bn和Xi-Xj≤-an两个不等式，分别用两条弧Xj→Xi和Xi→Xj表示，前者权重为bn，后者权重为-an，得到一个一般的加权有向图，称为STN的距离图(Gd)。STP，STN，Gd之间的转换如图1所示，三者之间的关系实质上是等价的[2]。

图1 STP，STN，Gd之间的转换关系Fig.1 Transformation relationship among STP, STN and Gd

遥感卫星具有载荷多、并行工作需求多样化等特点，卫星各分系统、单机、部件按照一定资源约束、时间约束协调工作的结果，即组成遥感卫星的工作模式设计。利用STN，可将遥感卫星工作模式设计问题抽象为简单时间问题，求解得到设计结果。

1.2 工作模式动作分解

在不同工作模式下，参与工作的星上设备或装置是不同的。驱动星上设备工作或停止工作的过程定义为一个“动作”，这样一次工作模式可分解为多个不同动作的集合。表1给出了通用遥感卫星不同工作模式所包含的动作。在每个工作模式下，各种动作之间都有特定时序约束。该约束一般包括动作本身需要持续的时间和相对基准动作的时间两个方面。遥感卫星通常对于设备启动、姿态机动、天线预置等动作要提出持续时间的要求；对于有先后时序要求的不同动作，如顺序开机、单向数据传输等，需要提出相对基准动作的时间约束。表2给出了不同工作模式下各动作时序约束的典型值。

表1 不同工作模式包含动作列Table 1 Actions contained in different working modes

表2 不同动作时序约束Table 2 Timing constrains of different actions

1.3 应用STN的时间表示和推理

下面介绍依据任务时间约束关系建立STN的方法。首先，根据不同工作模式，用时间点变量或区间变量表示任务中的动作，用箭线表示时序关系，得到定性约束网络。其次，根据具体约束把时间区间变量转化为时间点变量，并把定性约束转化为定量约束，为后续时间约束一致性检验与冲突处理等工作提供前提模型。常见的定量约束及其STN表示如表3所示。

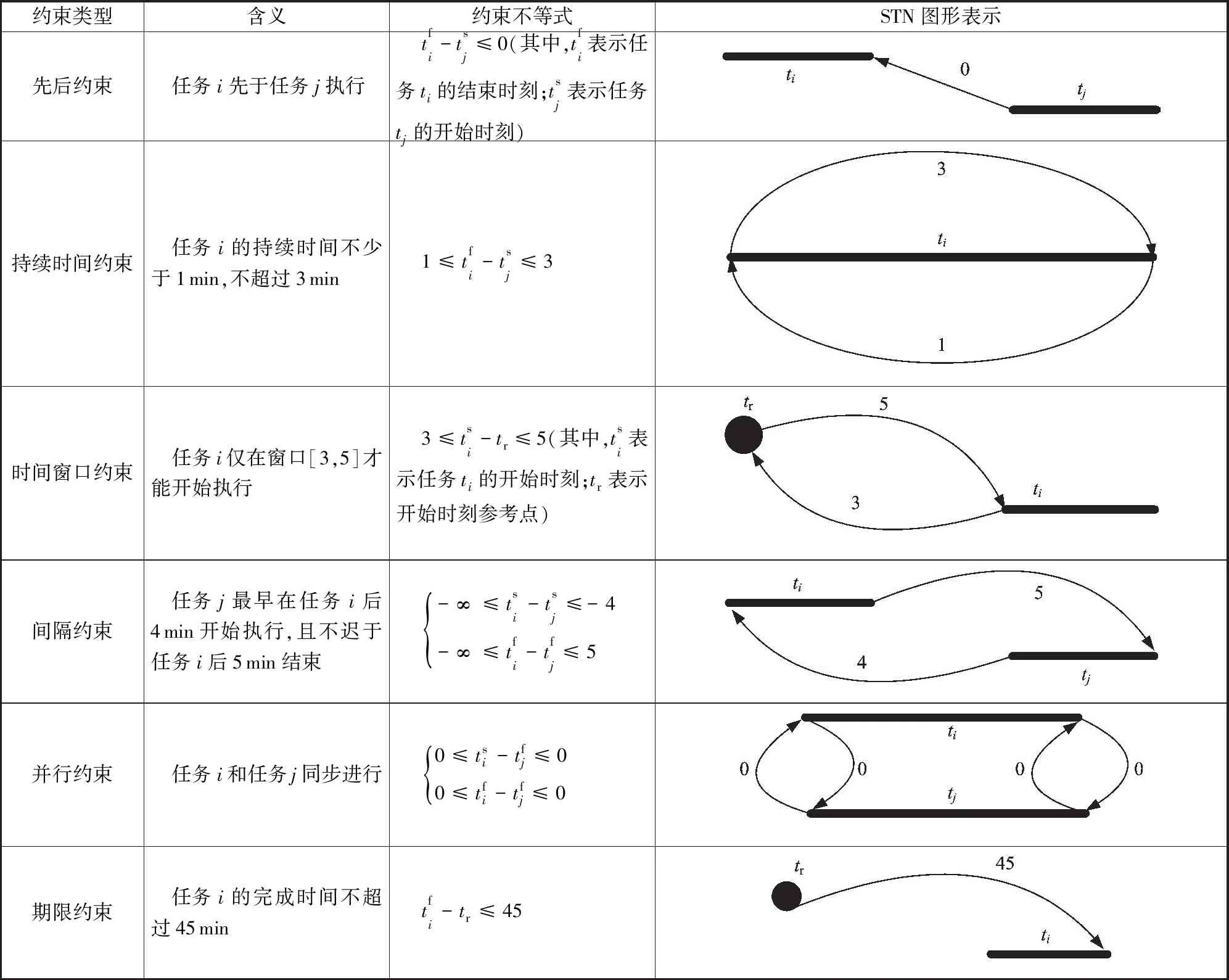
表3 STN图形表示示例Table 3 STN graphic examples

1.4 时序设计中时间冲突处理

STN时间网络模型是一种用于描述任务之间时序关系的加权有向图，具有表达能力强、计算方便和便于时间管理等优点[2]。应用STN时态表示模型和基于Gd的时态推理方法，提出时间冲突检测方法。Gd有向边的权值可正可负，可以很好地表示STN的时间约束关系，进行负环检测。每个STN都对应一个Gd，对STN的时间冲突检测实际上转化为Gd来研究。Floyd-Washall算法[9]可用于计算Gd中任意两点间的时间最短路径，得出最短路径矩阵。依据最短路径算法的性质，如果对角线出现负数，说明有负环存在，判定方案有时间冲突；否则，进一步优化方案。最后，利用最短路径矩阵计算Mij(任务i和任务j时间约束范围)，以此优化任务时间方案[10]。

遥感卫星工作模式时序冲突检测方法描述如下。

(1)建立遥感卫星工作任务时序关系的STN,对卫星任务计划进行建模。

(2)转化STN对应的Gd，利用Floyd-Washall算法计算最短路径矩阵，若对角线出现负数，转入步骤(3)；否则转入步骤(4)。

(3)搜索冲突路径节点并输出。

(4)计算Mij，按照任务要求的开始时刻和执行任务允许的时间范围，优化时间方案。

最短路径是图论研究中的一个经典算法问题，一般来说，就是从给定的网络中找出任意两点之间距离最短的一条路径。Floyd-Washall算法是计算任意两点间最短路径的较好算法[9]，主要计算最短路径矩阵和前驱矩阵这两个参数。其中，最短路径矩阵可以用来表示图上任意两个时间节点的最短路径，前驱矩阵可以表示最短路径的全部节点的时序关系。Floyd-Washall算法可求得每对顶点之间的最短路径，其中权可为负值。Floyd-Washall算法的描述见图2。

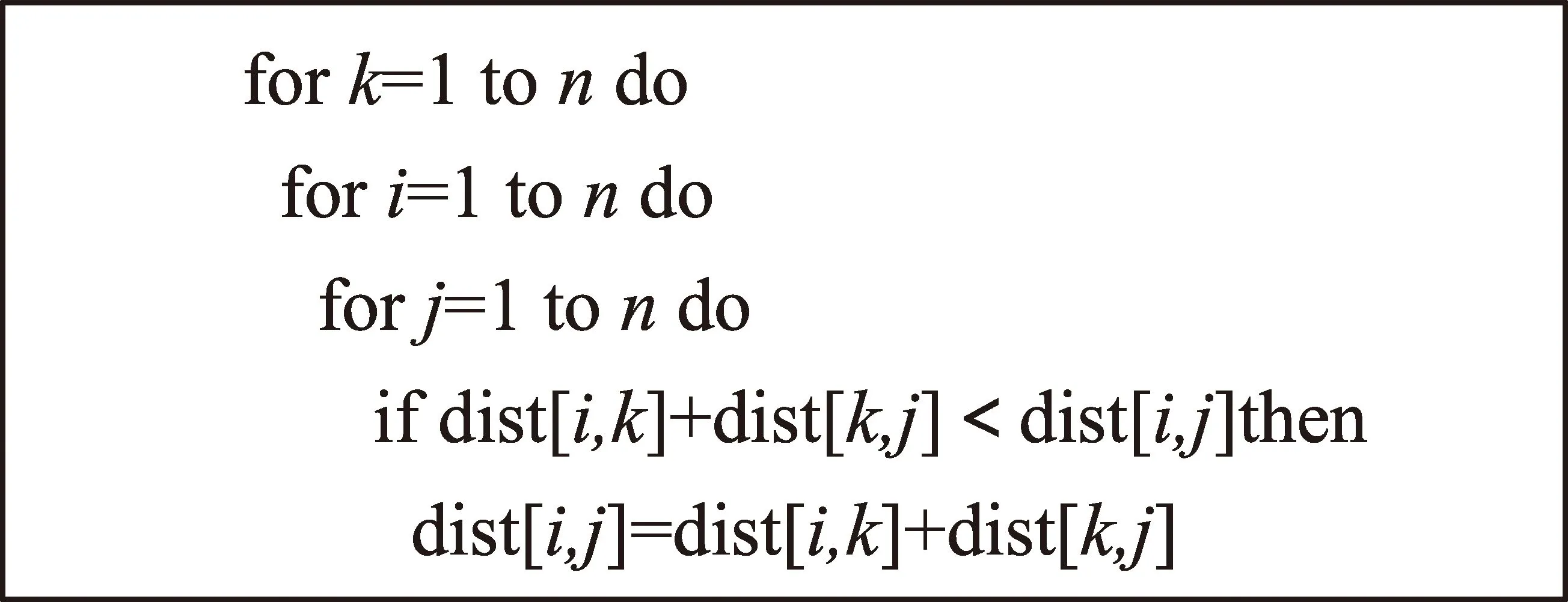
注：n表示任务数量；i表示起点任务；j表示终点任务；k表示中间某任务；dist表示任务时间节点间路径距离。

2 高分七号卫星应用实例

2.1 工作模式STN图形建立

依据表2动作时序约束，本节将以记录模式为例建立高分七号卫星的STN图形，如图3所示。记录模式下对应的Gd如图4所示。图中1，2，3等号码代表的是表1和表2中的动作编号。

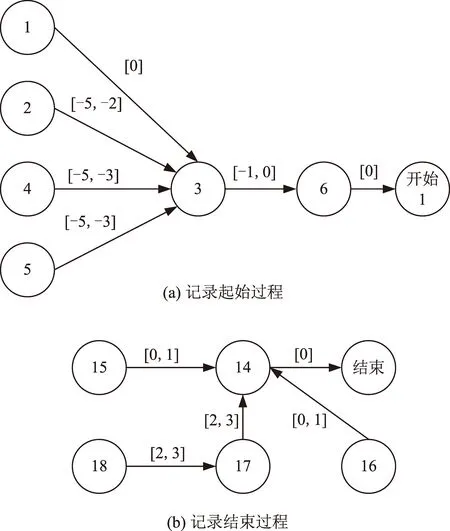
图3 记录模式的STN图形Fig.3 STN graphic of recording mode

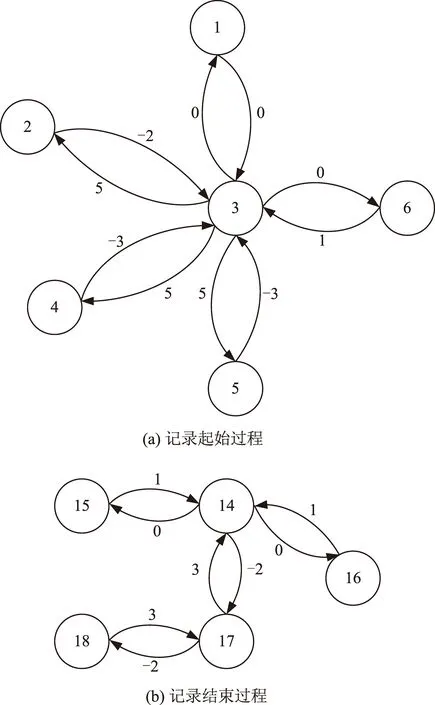
图4 记录模式的GdFig.4 Gd of recording mode

2.2 冲突检测和分析

对于记录模式下的Gd，可以得出任意两点的最短距离矩阵，如表4和表5所示，可得记录起始过程和记录结束过程动作间有向边的取值范围，如表6和表7所示。

表4 记录起始过程Gd的最短路径Table 4 Shortest Gd path of record starting process

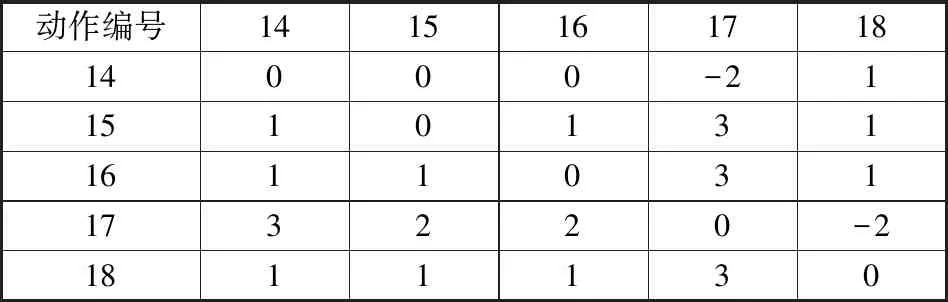
表5 记录结束过程Gd的最短路径Table 5 Shortest Gd path of record ending process

表6 记录起始过程动作间有向边的取值范围Table 6 Value range of directed edge between actions of record starting process

表7 记录结束过程动作间有向边的取值范围Table 7 Value range of directed edge between actions of record ending process

例如图5记录起始、结束的路径中共存在9个闭环，均由2个节点组成，经计算权值相加均大于或等于0，因此不存在负环，表明上述路径不存在冲突。可见，本文方法将高分七号卫星各工作模式中多项动作的时序设计工作由原有的人工手动设计，升级为通过STN来表示动作之间的时间约束并验证求解的过程。相比原有传统遥感卫星的设计方法，本文方法更适用于解决复杂卫星系统的情况，可由算法保证设计结果中不存在时间冲突，且设计结果为该约束条件下的最优解决方案。

3 结束语

本文提出了一种应用STN的遥感卫星工作模式设计方法，提出典型工作模式及其STN图形的表示形式，以及应用STN时态表示模型的时态推理方法，得出了时间冲突检测、任务起始时刻和执行时间间隔的可行解。高分七号卫星的实用结果表明：本文方法能够应用STN图形实现遥感卫星工作模式时序设计和检测时序冲突，可有效辅助遥感卫星总体工作模式时序设计，对遥感卫星总体设计工作具有一定的参考价值。