短码长的五元最优局部修复码

张 茂, 李瑞虎, 宋 倩, 陈 刚

(1.空军工程大学基础部，西安，710051； 2.兰州市27支局30信箱55号，兰州，732750；3.75837部队，广州,510000)

在大数据和云存储系统的发展中，分布式存储系统技术起着重要的作用。在现代分布式存储系统中，简单的数据备份是解决节点错误所采用的最广泛的方法，例如三重备份[1]。随着数据量的急剧增加，备份这种方法的缺点被暴露了出来，纠删码出现在人们的视野中[2-3]。2012年，Gopalan等人提出了一种新的纠删码——局部修复码(LRC)，它将数据修复转换成了构造满足一定条件的经典码的问题[4]：一个局部度为r的[n,k,d]线性码被记为[n,k,d;r]，其最小距离满足界：

(1)

这个界被称为Singleton形界，达到这个界的LRCs被称为最优LRCs。

关于最优LRCs，前人已经做了很多工作[5-19]。目前，在二元、三元域上最优LRCs的研究已经取得了一定进展，但在其他域上还有广阔的发展空间。二元最优LRCs的最小距离不大于4[7]，三元最优LRCs的最小距离为2，3，4，5和6[8]。2014年，文献[6]给出了四元域上d=3,r=3,4的最优LRCs。文献[5]和[11]、[9]、[14]和[17]分别给出了n≤q时、r+1|n时和d≤5时最优LRCs的构造。利用二元恒重码，文献[19]构造了4类距离为5和6的最优LRCs。当r≥d-2且r+1|n时，文献[18]给出了4类距离不小于7的最优LRCs。文献[12]运用群论构造了大域上的最优LRCs。关于最优LRCs的码长的界在文献[10]和[16]中给出。存在一些研究一般域上最优LRCs的论文结果涉及到五元域，具体的码见表1。

表1 文献涉及到五元最优LRCs的结果

对于参数为[n,k,d]的q元线性码，如果参数为[n,k,d+1]的码不存在，则称该q元码为最优的。文献[20]中已经讨论了3维和4维最优码的局部度，其中得到的10个码长不大于12的局部修复码的参数达到了Singleton形界。由于小域上的LRCs具有编解码复杂度低和易于实现等优点，鉴于以上工作，继续构造了大量新的最优LRCs。文章的主要结果如下：

1)当n≤12,2≤k≤n-1,[n,k]≠[7,2],[9, 2]和[11,2]时，对于任意的距离最优的线性码[n,k,d]均可构造为最优[n,k,d;r]LRCs；

4)存在以下局部度为1的最优LRCs：[6,2,4;1],[10,3,6;1],[8,3,4;1],[6,3,2;1],[8,4,2;1],[10,4,4;1],[12,4,6;1],[10,5,2;1],[12,5,4；1]。

以上所有的最优LRCs均由最优码构造。其中1)～3)中的LRCs是距离最优的，4)中的LRCs不是距离最优的。

1 预备知识

首先，为了便于叙述作以下标记：

记[n]={1,2,…,n}；1n和0n各自为长度为n的全1和全0的行向量；对于矩阵A，m个A的并置(A,A,…,A)记为mA。

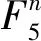
记a=(a1,a2,…,an)，向量a的Hamming重量定义为向量a中非零分量ai(i∈[n])的个数。如果C中所有非零码字的最小Hamming重量为d，则d称为码C的最小距离，记为C。

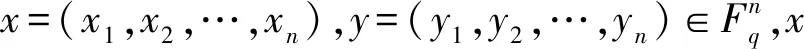
记线性码C=[n,k,d]。对任意的c=(c1,c2,…,cn)∈C，若第i个码元ci可以由其他个码元修复，则称ci的局部度为r。如果C中所有码元的最大局部度为r，则称码C的局部度为r。

线性码的局部度可以根据生成阵和校验阵通过如下方法来判断：

引理1[4]记G=(g1,g2，…，gn)为码C=[n,k,d]的一个生成阵。对于任意的rAi⊆[n]/{i}，如果存在最大为r的集合Ai⊆[n]/{i}，使得gi是gj(j∈Ai)的线性组合,则码C的局部度为r。

我们运用引理1～3来确定接下来构造得到的码的局部度，构造所用到的最优码见文献[22]。

2 由k≤4的距离最优的线性码构造LRCs

显然由1n=(1,1,…,1)可得到平凡码[n,1,n;1]和[n,n-1,2;n-1]。本节将由生成阵构造k≤4的最优LRCs。

2.1 由MDS码构造最优LRCs

定理1存在以下最优LRCs：

1)[6-i,2,5-i;2]和其对偶码[6-i,4-i, 3;4-i],(0≤i≤3)；

2)[6-j,3,4-j;3]和其对偶码[6-j,3-j,4;3-j],(0≤j≤2)；

3)[2s,2,2s-2;1],[2s,3,2s-4;1],(3≤s≤ 6);[12-2u,4,6-2u;1],(0≤u≤2)和[12-2v, 5,4-2v;1],(0≤v≤1)。

证明构造如下2个生成矩阵：

易证明G2×6生成[6,2,5;2]码，G3×6生成[6,3, 4;3]码。

1)当0≤i≤3时，删除G2×6矩阵的最后i列可得到G2×n=G2×(6-i),n=6-i(n≥3)。G2×n生成最优LRCC2×n=[n,2,n-1;2]，其对偶码为[n,n- 2,3;n-2]。由此可得到最优LRCs[6,2,5;2],[5,2, 4;2],[4,2,3;2],[3,2,2;2],[6,4,3;4],[5,3,3;3],[4,2,3;2]和[3,1,3;1]。

2)删除G3×6矩阵的最后j列(0≤j≤2)可得到矩阵G3×n=G3×(6-j)(n=6-j)。G3×n生成最优LRCC3×n=[n,3,n-2;3]，其对偶码为[n,n-3, 4;n-3]。由此得到最优LRCs[6,3,4;3],[5,3,3;3], [4,3,2;3],[6,3,4;3],[5,2,4;2]和[4,1,4;1]。

3)令G2×2m=(G2×m,G2×m),G3×2m=(G3×m,G3×m),(3≤m≤6)，可得到最优LRCs[2m,2,2m-2;1]和[2m,3,2m-4;1]。同样，可构造最优LRCs [2m,4,2m-6;1],(4≤m≤6)和[2m,5,2m-8;1] (5≤m≤6)。由此可得到最优LRCs[12,2,10;1], [10,2,8;1],[8,2,6;1],[6,2,4;1],[12,3,8;1],[10,3,6;1],[8,3,4;1],[6,3,2;1],[8,4,2;1],[10,4,4;1],[12,4,6;1],[10,5,2;1]和[12,5,4;1]。其中[12,2,10;1], [10,2,8;1],[8,2,6;1]和[12,3,8;1]是距离最优的。

2.2 由拟MDS码构造最优LRCs

本节将分别应用生成矩阵和校验矩阵构造3≤k≤4的最优LRCs。

定理2存在最优LRCs[n,3,n-3;2],(7≤n≤ 11)和[n,4,n-4;3],(7≤n≤12)。

证明根据文献[20]，G3×11和G4×12生成[11,3, 8;2]和[12,4,8;3]最优LRCs，其中：

1)当0≤i≤4时，删除G3×11的最后i列可得到以下最优码的生成阵：[11,3,8;2],[10,3,7;2], [9,3,6;2],[8,3,5;2]和[7,3,4;2]。

2)当0≤j≤5时，删除G4×12的最后j列可得到以下最优码的生成阵：[12,4,8;3],[11,4,7;3], [10,4,6;3],[9,4,5;3],[8,4,4;3]和[7,4,3;3]。

3 由k≥5的距离最优的线性码构造LRCs

给出了7个最优LRCs的校验阵，矩阵中横线上面的行代表局部度行。由这些矩阵可以得到其他最优LRCs。

3.1 由k≥5的拟MDS码构造最优LRCs

给出以下5个码的校验阵：

H2×12=(I2,I2,…,I2)

易知H2×12,H3×31,H4×26,H5×12,H6×12对应最优LRCs[12,10,2;5]，[31,28,3;24]，[26,22,4;19]，[12,7,5;5]和[12,6,6;5]。

定理3存在以下最优LRCs：

3)[26-t,22-t,4;19-t],(0≤t≤14),[11 -u,7-u,4;5-u],(0≤u≤2)；

(4)[12-v,7-v,5;5-v],(0≤v≤2)；

(5)[12,6,6;5]和[11,5,6;4]。

证明：

3)最优LRC[26-t,22-t,4;19-t]的校验阵H4×(26-t)可通过删除H4×26的最后t列(0≤t≤14)得到；继续删除H4×12的最后u列(1≤u≤3)，可得到H4×(12-u)，其对应最优LRCs[11,7,4;5],[10, 6,4;4]和[9,5,4;3]。

4)最优LRCs[11,6,5;4]和[10,5,5;4]的校验阵H5×(12-v)可通过删除H5×12的最后v列(1≤v≤ 2)得到；

5)删除H6×12的最后一列可得到H6×11和最优LRC[11,5,6;4]。

3.2 k≥5且k+d

证明 给出如下2个校验阵：

易知H7×12和H5×24对应最优LRCs[12,5,6;2]和[24,19,4;9]。

删除H5×24的最后i列(1≤i≤10)可得到参数为[23,18,4;9],[22,17,4;8],[21,16,4;7],[20,15, 4;7],[19,14,4;6],[18,13,4;5],[17,12,4;5],[16,11,4;5],[15,10,4;4]和[14,9,4;4]的LRCs。其中除了[23,18,4;9]外，其余均为最优的。

综上所述，定理1～4给出了前言部分的所有结果。

4 结语

本文研究了五元域上最优LRCs的构造，并给出了4类最优LRCs。除了参数为[12,2,10;1]的最优LRC，其他最优LRCs均满足最小距离d=3,4或n≤12时d≤8。文中给出了大量五元最优LRCs，然而，关于五元域上是否存在其他最优LRCs，仍需要进行进一步研究。