自适应克隆选择算法在等效系统拟配中的应用

段效聪， 徐浩军， 王国智， 李 哲， 吴喜杰

(1.空军工程大学航空工程学院， 西安， 710038； 2.95960部队， 西安， 710089)

从20世纪70年代开始，以F-16战斗机和空客A320为代表的现代先进飞机开始使用电传操纵系统(FBWS)，极大提高了飞行性能，同时解决了超音速战斗机固有稳定性不足的问题，但也使得描述飞机动力学的数学模型阶次较高[1]，许多附加模态难与飞机的长短周期模态相区分，无法直接评定其飞行品质，因此军用规范MIL-F-8785C和MIL-HDBK-1797中引入了等效系统的方法，并给出了相应的规定。

最小二乘法[2-4]因其使用过程简便，在工程实际中被广泛应用，但不同的初值选取会对拟配结果产生较大的影响，且拟配精度不高，甚至拟配曲线发散，不利于飞机设计过程中飞行品质的评价。近年来许多智能算法被应用到等效系统拟配中，如混沌差分进化算法、遗传算法、NSGA-II算法等[5-9]，仿真结果表明在满足失配度要求的同时可以解决传统拟配算法受初值选取影响较大的问题，但也存在计算效率低、收敛过程慢的缺点。

克隆选择算法(Clonal Selection Algorithm，CSA)是由Jerne提出的一种免疫算法(Immune Algorithm，IA)，它借鉴人体在外界抗原感染下产生抗体，抗体通过克隆、变异过程更新抗体群，并抵抗外界抗原侵入的原理[10]，设计出求解函数优化的算法，实现自我学习、全局寻优的功能。研究人员将克隆选择算法应用于现代制造中柔性作业车间调度、无人机多机协同航路规划、图像聚类等问题[11-13]中，并对该算法进行了优化改进，在工程应用中取得了较好的结果。

本文首先进行了人-机-环闭环系统的建模，在此基础上将克隆选择算法应用于等效系统拟配的仿真分析中，采用GJB 2874—97中规定的失配包络线对拟配结果进行检验，并与最小二乘法得到的拟配结果进行比较，使用克隆选择算法得到的低阶等效系统满足要求且精度更高，利用操纵期望参数CAP和(ωn1·Tθ2)及ζn1对飞机纵向飞行品质进行评价，飞行品质评价结果满足飞机设计要求。

1 人-机-环闭环系统建模

驾驶员在特定的飞行环境中操纵飞机从而构成复杂的人-机-环闭环系统，飞行安全受到除飞机本体外包括驾驶员操纵、飞行环境等因素的影响，因此建立包含驾驶员操纵行为及外部环境因素的高阶系统是飞行品质评估的基础。

1.1 驾驶员操纵行为建模

本文驾驶员模型采用补偿操纵模型，如图1所示。即驾驶员全神贯注地操纵飞机时，将根据飞机运动姿态误差值，及时调整驾驶杆输入，使飞机对指令的响应与飞行任务相匹配。

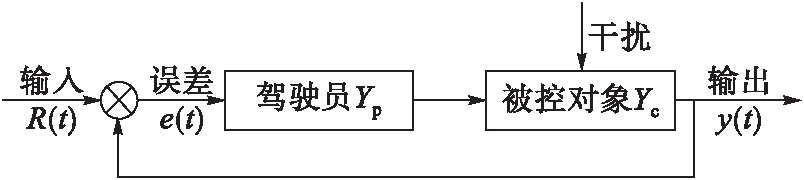
图1 驾驶员补偿操纵模型

航线飞行时飞机姿态变化较为平稳，纵向短周期频率通常小于10 rad/s，进行飞行品质分析时一般采用驾驶员传递函数模型[14]，对于大多数工程应用可以采用下式近似：

(1)

参数kp、TL、TN、τ的取值范围参考文献[14]。

1.2 飞机本体及纵向电传操纵系统建模

1.2.1 飞机本体建模

忽略扰动运动中高度变化引起的外力和力矩的影响，利用“小扰动”条件将飞机运动分离成横向与纵向扰动运动，可以采用有因次矩阵形式的状态方程来表征飞机纵向扰动运动，如式(2)所示：

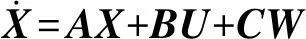
(2)

式中：状态矢量X=[ΔV Δα ΔqΔθ]；控制矢量U=[ΔδeΔδp]；湍流矢量W=[wxwywyx]；A为纵向系统矩阵；B为控制矩阵；C为扰动矩阵。

1.2.2 纵向电传操纵系统建模

俯仰角速率指令构型可以使飞机具有良好的俯仰指向特性，文中背景飞机操纵系统采用该种构型控制率，其结构如图2所示，以俯仰角速率q作为机动指令，现代战斗机多采用放宽静稳定性设计，迎角α反馈可以补偿静稳定性，外环机动指令反馈回路和比例-积分环节可以消除俯仰角速率的稳态误差，并提供前向增益以提高飞机操纵性。控制率中指令变量为俯仰角速率增量指令qcmd，有4个可调增益Kq、Ki、Kα、Kp。

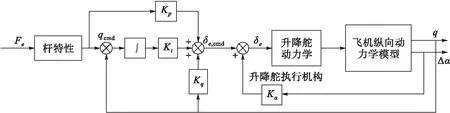
图2 俯仰角速率指令构型结构图

1.2.3 舵面作动器模型

本文对算例飞机纵向进行等效系统拟配，主要操纵舵面为升降舵，其作动器动力学模型[15]可以采用一阶惯性环节、速率限制器和位置限制器加以表征，如图3所示，T为一阶惯性环节的时间参数，一般取30。

图3 舵机动力学模型示意图

2 克隆选择算法

2.1 克隆选择算法基本原理

克隆选择算法的基本原理[16]为：根据参数变化范围随机产生N个抗体，构成初始抗体群P。根据抗体群亲和度值f进行克隆扩增，形成抗体群C并记录此时f值。对抗体群C进行变异形成抗体群C*，若抗体群C*的f值不满足结束条件，从抗体群C*中选取d个f值较高的抗体替换P中d个f值较低的抗体，对抗体群进行更新。经过若干代的克隆选择，得到最优的抗体，在整个过程中能够根据抗体对抗原的亲和度值f调节抗体的变异率和迭代次数。整个拟配流程见图4。

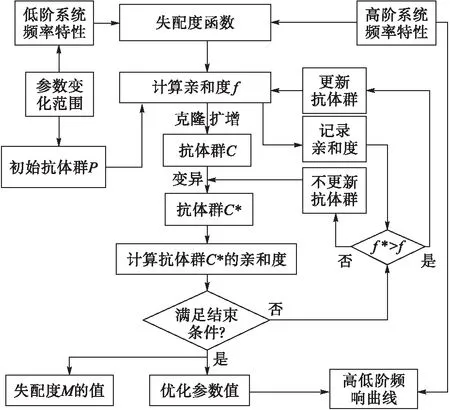
图4 自适应克隆选择算法拟配流程图

2.2 基于自适应克隆选择算法的拟配流程

Step1根据参数变化范围随机产生N个抗体，构成初始抗体群P，设定计算过程最高迭代次数。

Step2M为失配参数，计算过程如式(3)，根据f=1/M得到抗体群的f值并记录。

K[Φhos(ωi)-Φlos(ωi)]2}

(3)

式中：n为拟配频率范围内所选取的点数，取值30；ωi为拟配频率点，在0.1～10 rad/s的范围内按对数坐标n等分选取；Ahos，Φhos分别为高阶系统频率特性的幅值和相位；Alos，Φlos分别为低阶等效系统频率特性幅值和相位；K一般取0.017 45 dB/(°)。

Step3对抗体群P中的抗体进行克隆扩增操作，得到抗体群C。抗体的克隆数n与其本身的f值有关，计算过程如式(4)所示。

(4)

式中：nmax为给定的最大克隆常数；f为要进行克隆的抗体亲和度值；fmin为抗体群中最低的亲和度值；favg为抗体群平均亲和度值，int((f-fmin)/(favg-fmin))表示向下取整。

Step4对抗体群C中的抗体进行单点变异，得到抗体群C*。抗体变异率pm计算如式(5)所示，若ffavg，则抗体变异率依据式(8)进行计算。迭代次数越接近最大设定次数，pm值就越小。在寻优初始阶段及寻优后期，通过不同的变异率使其快速移动到抗原(全局极大值点)附近，并逐渐接近全局最优解，克服全局寻优和局部求精的矛盾。

(5)

式中：pm-max为给定的最高变异率；pm-min为给定的最低变异率；Gmax为最大迭代次数；G(i)为当前迭代数。

Step5计算抗体群C*的f*值并与初始抗体群的f值进行比较，如果f*>f，就保留此次变异的抗体，否则重新进行变异。这样可以保证在变异算子中引入新的、优良的抗体，避免计算过程中部分抗体退化的现象，可以提高算法的收敛速度。

Step6从抗体群C*中选择d个f值较高的抗体替换P中d个f值较低的抗体。更新抗体个数d的计算如式(6)所示，在寻优初始阶段及寻优后期，随着抗体群的进化，抗体群f值相差逐渐减小，均值逐渐增大，使得在寻优初始阶段被更新的抗体数量多，d值较大；寻优后期抗体被更新数量减少，d值较小。

(6)

式中：dmax为给定抗体最大更新数量;dmin为给定抗体最小更新数量。

Step7终止条件，满足终止条件时迭代计算结束，输出失配度M的值以及优化参数值。

3 仿真计算及飞行品质分析

算例飞机为常规气动布局，对于飞机纵向通道，以给定的俯仰角ϑ和俯仰角速率q低阶等效传递函数分别对长短周期进行拟配，此时飞机为巡航飞行阶段。依据规范MIL-HDBK-1797，纵向低阶等效系统长短周期拟配的模型如式(7)和式(8)所示。

长周期：

(7)

短周期：

(8)

式中：e-τϑs在参数辨识时对纯延迟环节作一阶伯德描述[17]。

如式(7)和式(8)所示，共有8个待拟配参数Kθ、Tθ1、Tθ2、ζn1、ωn1、ζn2、ωn2、τϑ。各参数的初始范围分别取Kθ∈[10,15]、Tθ1∈[0.1,10]、Tθ2∈[0,10]、ζn1和ζn2∈[0,2]、ωn1和ωn2∈[0,20]、τϑ∈[0,0.25]。

为满足仿真的精度要求，设置最高迭代次数为50次，初始抗体数目N取30。设定4个飞行状态为：①H=3 000 m，Ma=0.5；②H=5 000 m，Ma=0.6；③H=8 000 m，Ma=0.8；④H=8 000 m，Ma=1.2。在0.1～10 rad/s频率范围内进行拟配计算，计算结果见表1。

表1 等效系统拟配结果

由表1数据可见，设定的4种状态下计算得到的M值均满足规范中所规定的失配度不大于20的要求，表明在所选择的拟配频率范围内，高低阶系统的频域响应基本一致，满足规范MIL-F-8785C和MIL-HDBK-1797的要求。

以飞行状态②H=5 000 m、Ma=0.6为例，在第23次迭代计算中得到最优值，收敛速度较快。高阶系统、等效低阶系统和飞机本体的阶跃响应特性和对数幅频特性曲线分别如图5、图6所示。

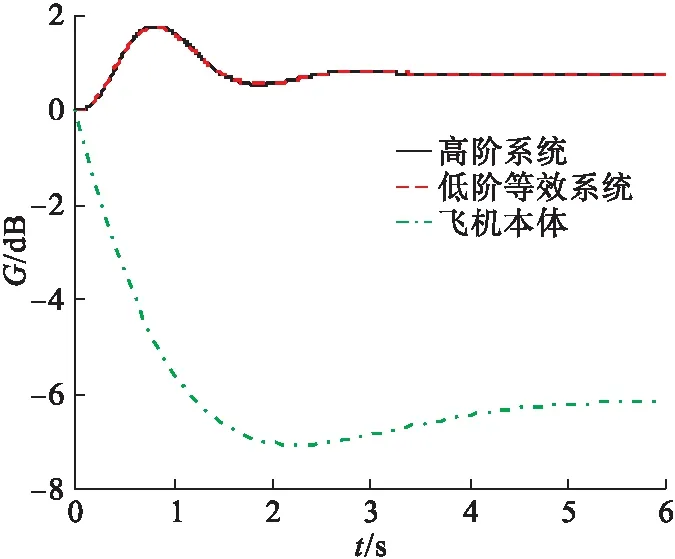
图5 高阶系统、低阶等效系统和飞机本体阶跃响应曲线图

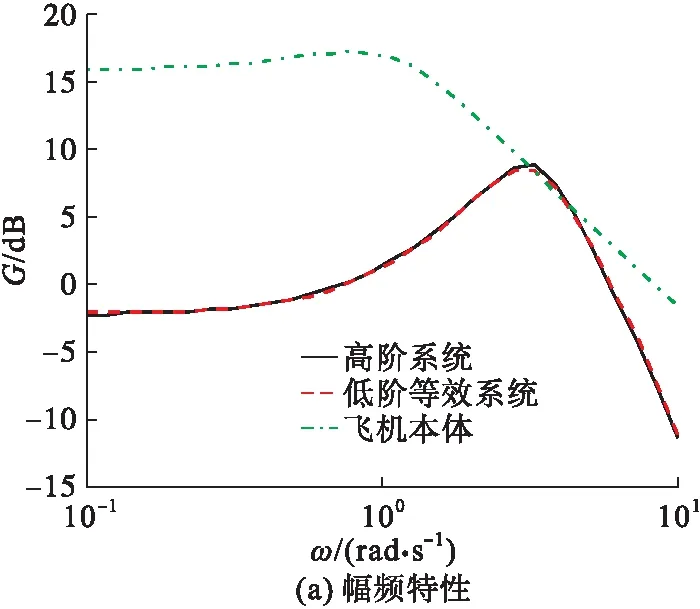
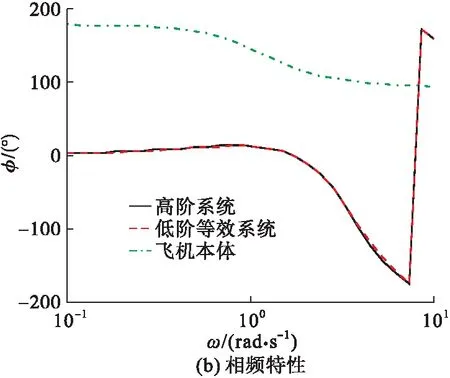
图6 高阶系统、低阶等效系统和飞机本体Bode图

由图5、图6可见：①飞机本体与高阶系统的对数幅频特性和阶跃响应特性相差较大，这说明在运用等效系统准则评价飞机的飞行品质时，需要考虑飞行状态的外部环境及驾驶员行为状态因素；②相较于飞机本体的阶跃响应，高阶系统的阶跃响应超调量小、调节时间快，这表明纵向控制增稳系统可以极大的改善飞机的动态特性；③在0.1～10 rad/s的频域范围内，高、低阶等效系统具有相似的对数幅频特性、相近的开环增益和绝对值相近的零极点，且时域内阶跃响应特性基本一致，从频域和时域的角度，都充分说明了运用自适应克隆选择算法辨识出的低阶系统参数精度高，高低阶系统拟配效果好。

选取相同的待拟配参数初值分别应用最小二乘法和自适应克隆选择算法进行等效系统拟配，得到的高、低阶系统的幅值失配包络图和相角失配包络图分别如图7、图8所示。在实际应用中，MIL-HDBK-1797建议[18]使用失配包络线来检验拟配精度是否满足标准。由图7、图8可见，在0.1～3 rad/s范围内，失配度均处于包络线范围内，但使用自适应克隆选择算法拟配精度高于最小二乘法。3～10 rad/s范围内，使用最小二乘法时出现了失配现象，使用自适应克隆选择算法未出现失配现象。在0.1～10 rad/s频率范围内，使用自适应克隆选择算法时失配度均处于失配包络线内，表明拟配结果是满足标准要求的，且拟配精度较高，受初值选取影响较小。

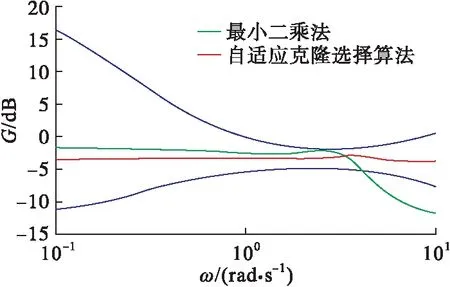
图7 幅值失配包络图

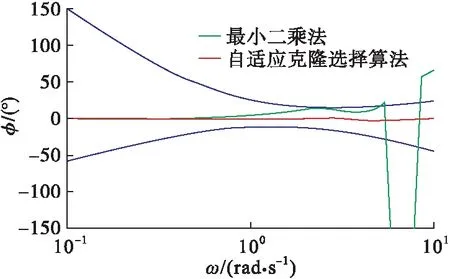
图8 相角失配包络图

在获得低阶等效系统参数后，可以利用2种方法对飞机纵向短周期飞行品质[19]进行评价：①依据CAP参数进行评价；②依据(ωn1·Tθ2)及ζn1进行评价。文献[1]中认为(ωn1·Tθ2)及ζn1对于衡量纵向飞行品质可以提供较好的相关性，(ωn1·Tθ2)及ζn1的组合确定了俯仰姿态频率响应的形状。

由拟配得到的低阶等效系统参数分别计算各种飞行状态下的CAP值、ζn1、τθ及ωn1·Tθ2，按照GJB185—86中相关规定从短周期频率要求、动态品质要求和俯仰响应要求评判其飞行品质，其结果分别如图9、图10、图11所示。

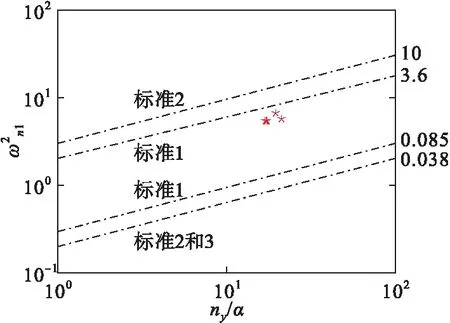
图9 短周期频率要求(航行阶段)

图10 短周期动态品质要求(B种飞行阶段)

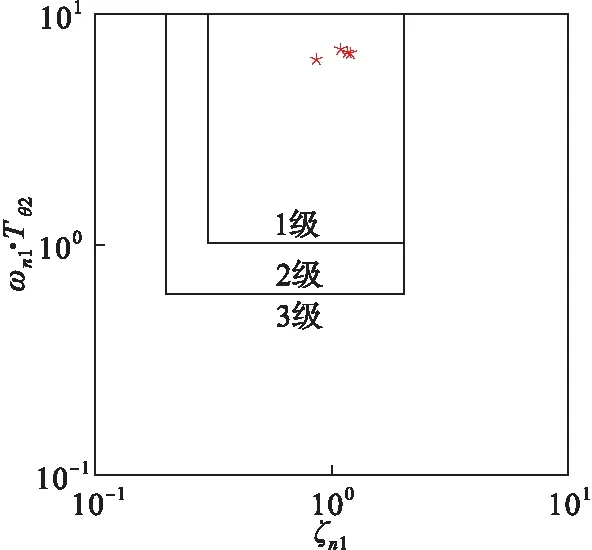
图11 短周期俯仰响应要求(B种飞行阶段)

由图9、图10、图11可以得到算例飞机在4种飞行状态下均达到一级飞行品质标准要求。

此外标准中规定对于各类型飞机及飞行状态等效时间延迟还应该满足以下条件：一级0.1 s；二级0.2 s；三级0.25 s。

对于算例飞机设定的4种飞行状态，等效时间延迟均满足一级飞行品质要求。

4 结语

本文提出了一种基于自适应克隆算法的等效系统拟配方法。以算例飞机在巡航阶段4种飞行状态下的俯仰角ϑ和俯仰角速率q双拟配过程为例进行计算，并与最小二乘法得到的结果进行比较，仿真结果验证了该算法的有效性和可行性。在计算过程中通过抗体对抗原亲和度的不同自适应调节变异率，并利用寻优前后期变异率的变化逐渐接近全局最优解。算法对初值选取的依赖性小，结构简洁，拟配结果精度高，利用CAP参数、(ωn1·Tθ2)及ζn1对飞行品质进行评价在工程应用中容易操作。同时算法仍然存在一些可以改进的地方，如抗体群更新时随机性的选择，抗体群C*中退化抗体的处理等。