叶片式旋流畸变发生器生成旋流角的影响因素

王加乐， 程邦勤， 冯路宁， 李 军， 姚耀泽， 费晓文

(空军工程大学航空工程学院， 西安， 710038)

旋流畸变与总压畸变、总温畸变是进气道出口流场畸变的主要类型，对压气机的性能和稳定性会产生十分不利的影响，严重时甚至会导致发动机喘振。欲研究旋流畸变对发动机性能的影响，首先要获得旋流场，国内外学者对旋流场的获得方法开展了大量的研究。目前国内外较为成熟的获取旋流场的方法主要有三角翼法、旋流腔法和叶片法。

Genssler等人[1]最早利用三角翼来产生对涡旋流，并且发现通过调节三角翼的攻角可改变对涡旋流的强度。Pazur[2]和Schmid[3]等人在风洞中开展了相关的试验，并研究了对涡对压气机性能的影响。三角翼式的旋流畸变发生器制造成本低且加工简单，但它只能产生对涡旋流场，无法模拟其他样式的旋流场。Sheoran[4]和Bruce[5]设计了一种腔室型旋流畸变发生器，可通过改变进气方式、调节腔室调节板的尺寸位置等方法来产生不同结构样式的旋流场，主要有整体涡、对涡和偏移对涡等。但是腔室型旋流畸变发生器仍然无法模拟飞机在实际飞行中产生的复杂流场，并且很难对流场进行精准的控制，最终使得这种方法逐渐被放弃。早在Tornado战机研制后不久，国外的Genssler[1]等人便采用了类似发动机进口导流叶片的装置来产生旋流畸变，由于受当时工业水平的限制，Genssler设计的旋流畸变发生器采用的是直叶片，故获得的旋流场与目标流场有较大差异。Flitcroft[6]和Govardhan[7]设计了整体涡旋流畸变发生器，着重研究了旋流畸变对压气机性能的影响，并没有对畸变发生器产生流场的精度开展细致的研究。姜健等[8-10]设计的叶片式旋流畸变发生器，通过改变叶片的布局和构型产生了不同强度的整体涡、对涡以及偏移对涡。屠宝锋[11]设计了一款可调叶片式旋流畸变发生器，通过改变叶片的安装角以及叶片数目来改变旋流强度。上述叶片式旋流畸变发生器仅可产生一般样式的旋流场，没有利用叶片式旋流畸变发生器复现实际飞行中飞机内部的复杂旋流场，也没有目标流场，无法研究其畸变发生器获得的流场精度。随着旋流畸变研究的深入，对于能产生实际飞行中复杂旋流场的旋流畸变发生器设计方法的需求也更加迫切。Kevin[12]首次根据目标流场来反推畸变发生器的结构样式，并且随着现代制造工艺的提升和加工能力的极大提升，所设计的叶片式旋流畸变发生器也不再是独立叶片的组合，而是利用CAD技术将叶片融合在一起做成了旋流畸变网，其结构更加稳定，复现流场的精度更高。张磊[13]也做了相关的研究。虽然旋流畸变网结构稳定而且可复现任意结构样式的旋流场，但在设计过程中需反复调整叶片安装角和弦长等几何参数才能与目标流场吻合，耗费时间和精力过多，设计效率较低。

1 初始计算模型的设计

张磊[14]采用平面叶栅研究了气流转角与叶型安装角的关系，但其模型和实际情况贴合性不强。本文改用整体涡模型研究不同因素对旋流角生成的影响，如图1所示，本文在圆形截面中沿周向均匀布置12条叶片，采用此布局主要基于以下3点：①此种布局与大多数叶片式旋流畸变发生器的布局相同，均是在圆形截面中布置叶片；②可直观地观察叶片稠度与旋流角的大致关系；③可观察旋流角的均匀程度。

图1 整体涡旋流畸变网

数值模拟模型的叶型选用某型气体流动性能较好的可控扩散度叶型(CDA叶型)(见图2)来消除或抑制附面层分离，同时减小压力损失，以期望产生分布均匀的旋流角。初始模型的结构尺寸如图1所示，外圆半径300 mm，内部圆环半径30 mm，畸变段长度300 mm，模拟的是空军工程大学低速轴流压气机试验台[15]的结构尺寸。

图2 旋流畸变网采用的叶型

2 数值计算方法

2.1 几何模型

本文计算域的设置是根据空军工程大学等离子体实验室单级低速轴流压气机试验台(图3)设定。计算域共分为前置管道、畸变段和后置管道，见图4。其长度分别为1 800 mm、300 mm和800 mm，管道直径为600 mm，AIP(气动交界面)初始设置在畸变段出口一倍管径600 mm处。

图3 低速轴流压气机实验系统

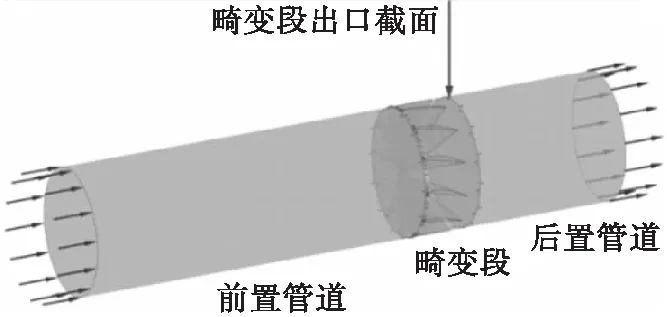
图4 计算域

2.2 求解方法及网格无关性验证

计算采用ANSYS CFX 17.0，进口边界条件为总压101 325 Pa，总温288 K，出口边界条件初始设置质量流量6.5 kg/s，壁面采用绝热无滑移边界条件，计算采用k-ω湍流模型，收敛准则设置为各个待求解量的相对变化值下降到10-5，并监控进出口流量平衡情况。整个计算域网格总数达到900万，计算在1台48 G内存16核的计算机上进行。

针对计算域特点，前置管道和后置管道采用O型结构网格，畸变段采用正四面体非结构网格，对叶片前后缘进行线加密，针对中间涡核位置结构密集复杂特点，创建一个加密区。计算时共划分了4套网格，以总压恢复系数σ(旋流畸变发生器进出口截面总压比)为准则参数，计算结果如表1所示，当网格数量达到600万时，继续增加网格数量对计算结果的影响可忽略，最终畸变段网格数量650万，近壁面处网格y+<3，满足精度要求。

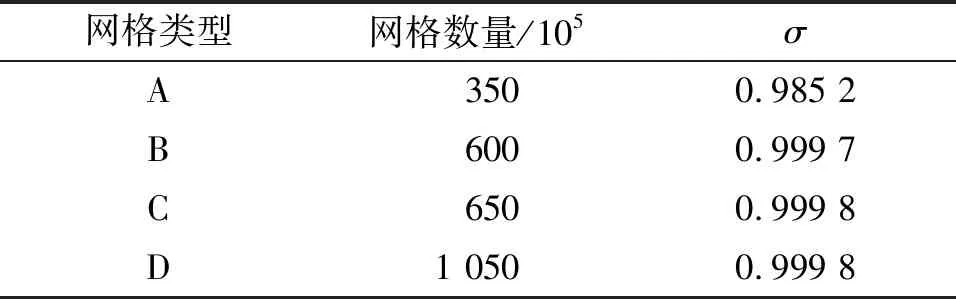
表1 网格数量与总压恢复系数

3 结果分析

当前旋流畸变评价指标主要采用AIR-5686[16]给出的标准，此标准基于旋流角，采用3个指标和2个子参数来评价旋流畸变，其中旋流角是最基础的评价指标,旋流角α的定义式为：

α=arctan(Uθ/Ux)

(1)

式中：Uθ为AIP上某点周向速度分量；Ux为AIP上某点轴向速度分量。

3.1 稠度的影响

为探究稠度对旋流角生成的影响，设置了等弦长为100 mm，弯角分别为5°、10°、15°和20°的4个整体涡模型，首先在SolidWorks中绘制模型，采用ANSYS ICEM进行网格剖分，计算采用ANSYS CFX，仿真计算结果如图5所示。可见等弦长模型产生的旋流角很不均匀，并且随着稠度的减小，产生的旋流角随之减小。

图5 不同角度的整体涡旋流畸变网速度矢量和旋流角云图

从图5可见，随着半径的变化，即叶片稠度的变化，AIP上产生的旋流角度随之变化。在流场中沿径向设置一条线段(见图6)，可得到线上任意位置处的旋流角，初步得到稠度与AIP旋流角的大致关系如图7所示。

图6 采样线

图7 等弦长模型稠度与旋流角关系图

随着稠度的增加，旋流角度变大，考虑到气流向下游发展的过程中会相互掺混影响，采样位置与AIP相应位置的旋流角并非是真实对应的关系。为寻求更精准的稠度与旋流角的关系，将同一个整体涡旋流畸变发生器的所有叶片设置成同一稠度，将AIP的平均旋流角认为是该稠度对应产生的旋流角。

图7中发现，当稠度小于1时，旋流角复现效率较低，当稠度大于2时，稠度的变化对AIP上旋流角变化影响不大，故设计模型时，将叶片稠度范围设置为1～2，间距为0.1，共11个稠度，每个稠度对应设置叶片弯角为5°、10°、15°和20°的整体涡模型，这样共计建立44个整体涡模型。

由于整体涡模型中间位置未布置叶片，且未布置叶片区域的半径为0.03 m，考虑到该区域无法反映真实的旋流角，如图8所示，选取AIP上半径0.06～0.3 m的圆环上旋流角的平均值认为是该稠度下产生的旋流角度。经计算后，获得不同弯角的整体涡模型，在不同稠度下所获得的旋流角角度见图9。

图8 采样环

从图9可以看出，随着稠度的增大，AIP上的旋流角随之增大，且叶片弯角越大的，旋流角随稠度增大的越多。

图9 等稠度模型稠度与旋流角的关系图

将不同弯角模型获得的旋流角除以对应叶片弯角后定义为单位旋流角，则不同弯角条件下，稠度与单位旋流角的关系如图10所示，将4组单位旋流角取平均后，(红线)可拟合为式(2)。

α=(0.044 9τ3-0.268 1τ2+0.597 2τ+0.459 7)β

(2)

式中：τ为叶片稠度；β为叶片弯角。

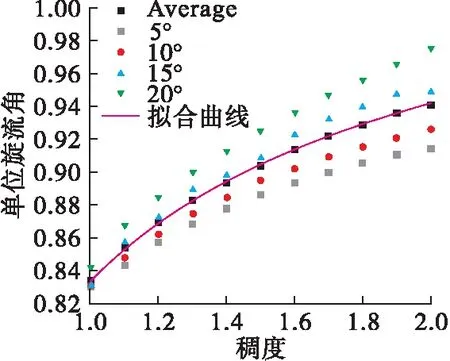
图10 稠度与单位旋流角的关系图

由于各曲线上旋流角与取平均后的曲线存在误差，经处理后发现，其误差近似为线性关系，式(2)变为式(3)，其中5°、10°、15°和20°曲线对应的系数B1、B0见表2。

α=(0.044 9τ3-0.268 1τ2+0.597 2τ+0.459 7+

B1τ+B0)β

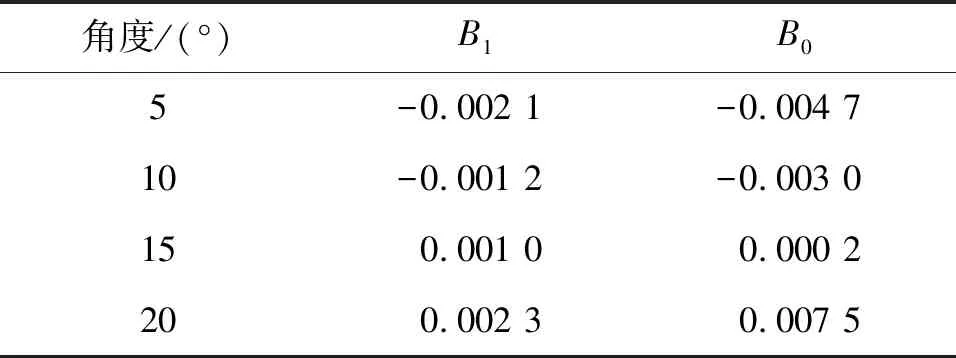
(3)

3.2 AIP选取位置的影响

观察图11可知，随着气流向下游的发展，旋流角逐渐变小，这是由于气流之间相互掺混造成的。

图11 单位旋流角发展趋势

为进一步衡量旋流角随着气流向下游发展的变化，在距离畸变段后每隔100 mm设置一个观测截面，第一个截面距离畸变发生器后的距离定义为单位距离D0，观测各截面上旋流角的生成情况，得出变化趋势如图11所示，将数据处理后发现，在任意相邻两截面，下一截面旋流角与该平面旋流角值之比为0.998。式(3)为AIP上旋流角表达式，则在畸变段出口截面到AIP之间任一截面的旋流角可用式(4)表示。

α=(((0.044 9τ3-0.268 1τ2+0.597 2τ+0.459 7)×

(4)

式中：D为畸变段出口截面距离计算域进口的距离；R表示所选取的AIP距离计算域进口的距离；(R—D)表示所选取的AIP与畸变段出口截面的距离。

3.3 安装角增量的影响

从上文的研究中发现，稠度选取比较密集，相邻稠度之间对旋流角变化影响不大，故在此选取稠度1.1、1.5和2的12个整体涡模型来研究安装角增量对旋流角的影响。将所有模型均增大5°的安装角，得到旋流角增量如图12所示。

观察图12发现，叶片弯角相同的模型增大相同的安装角，发现叶片稠度越大，其旋流角增量越大，呈线性关系。

图12 旋流角增量与弯角关系图

从图13发现稠度相等的模型增大相同的安装角，叶片弯角越大，旋流角增量越大，且近似呈线性关系。

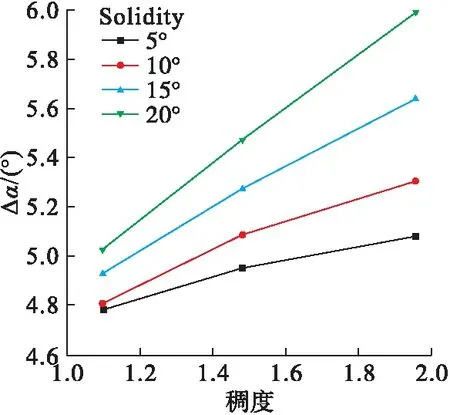
图13 旋流角增量与稠度的关系

3.4 马赫数的影响

选取叶片弯角为20°、叶片稠度为1.5的整体涡模型，将后置段出口反压分别设置为70 kPa、80 kPa、90 kPa以及95 kPa，对应气流流经畸变段后的马赫数为0.71、0.55、0.31以及0.06。距离畸变段出口截面每100 mm取一检测截面，发现旋流角与马赫数关系如图14所示。在亚音速阶段，旋流角和马赫数之间近似呈指数关系。这是由于随着马赫数越大，气流流动速度越快，气流运动越紊乱。不同马赫数的气流向下游发展相同的距离时，马赫数低的气流掺混更加均匀，旋流角相对较小。

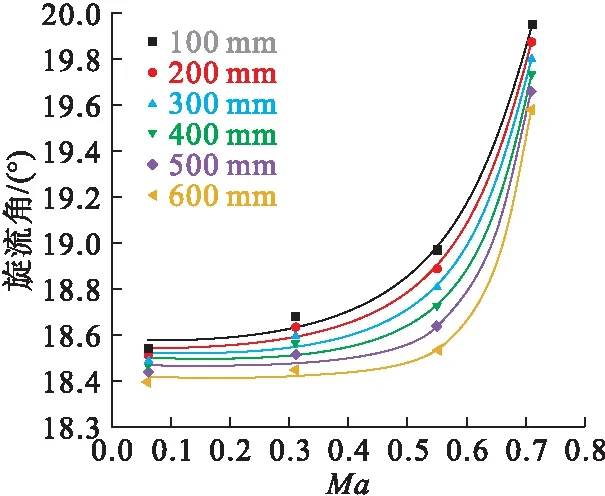
图14 不同截面下旋流角与马赫数关系图

3.5 畸变发生器直径的影响

选取弯角20°，稠度为1.5的整体涡模型，进口条件为总压101.325 kPa，总温288 K，出口设置反压80 kPa，分别将外径设置为200 mm，400 mm，计算结果如图15所示。可见管径在200～600 mm范围内，随着畸变发生器外径的减小，旋流角会随之增大，近似呈线性关系，通过图15纵坐标来看，畸变发生器的外径对旋流角的影响较小。综合考虑各类影响因素，旋流角的生成可用式(5)表示，此公式对叶片式旋流畸变发生器的高效率设计有一定参考价值。

(5)

式中：αPi为第i个截面的旋流角。

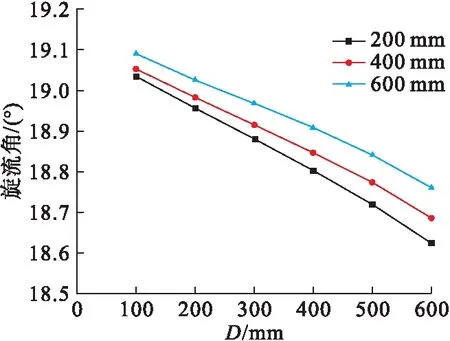
图15 不同管径旋流角向下游发展趋势

3.6 拟合公式有效性验证

利用所获得的拟合公式设计了标准对涡旋流畸变网(图16)，基于单级低速轴流压气机实验台(图17)开展试验测量验证，测量距畸变网出口截面下游600 mm截面的旋流角。

图16 对涡旋流畸变网的安装

图17 单级低速轴流压气机实验台系统

如图18所示，在每个测量截面布置3×12共36个测点，采用五孔探针测量出每个测点的总压、静压、气流迎角a和气流偏转角b，可计算获得每个测点的三维速度，最终可计算获得旋流角。试验在实验台设计转速3 000 r/min，流量6.5 kg/s的工况下进行，试验时大气温度293 K、大气压力101.050 kPa。

图18 测点示意图

在旋流场内设置3个测环(图19)，在3个测环上目标流场、CFD模拟结果以及试验结果的旋流角分布如图20(a)～(c)所示，其两两之间旋流角的误差如表3所示。

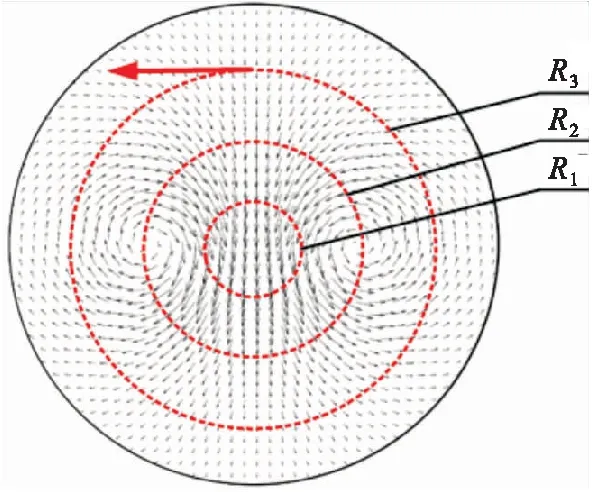
图19 测环示意图

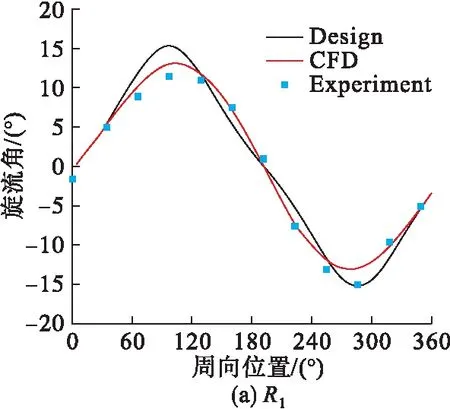
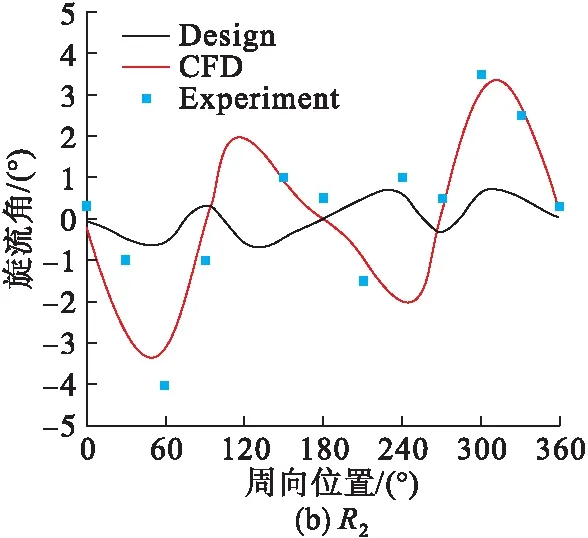
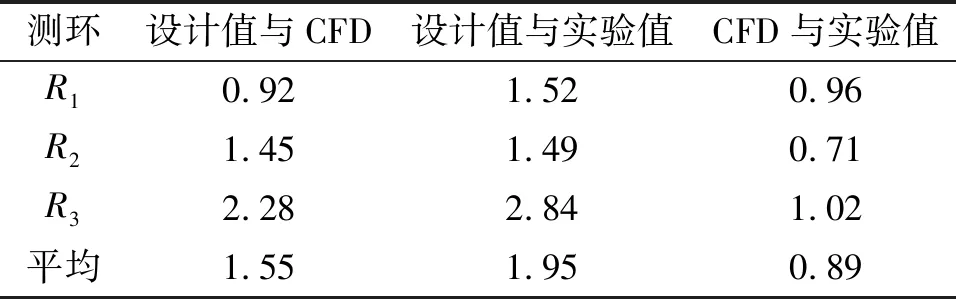
表3 目标流场、CFD以及试验结果的旋流角误差

从图中可以看出，在R1和R3测环上CFD模拟和试验结果与设计值吻合较好，在R2测环，由于叶片布置密集，且存在支撑结构的影响，导致CFD以及试验结果与设计值误差较大。

结果表明，利用拟合公式设计的对涡旋流畸变网较高精度地复现了目标流场的旋流角设计值，只需在误差较大区域进行优化设计，即可高精度模拟目标流场，有效缩短了设计周期和时间成本。

4 结论

1)本文从整体涡旋流畸变网出发，研究叶片生成旋流角的影响因素，并运用拟合公式设计对涡旋流畸变网，经试验验证后，拟合公式可信度较高，可将结论推广至S弯进气道出口等旋流畸变网的设计中。

2)随着气流向下游发展过程中，气流掺混更加均匀，旋流角逐渐变小；增大相同安装角，稠度越大、叶片弯角越大，则旋流角增量越大，且呈线性关系；畸变发生器外径尺寸越小，生成的旋流角越大，近似呈线性关系；马赫数在一定范围内对旋流角影响呈指数关系，马赫数越大，生成的旋流角越大。

3)稠度以及叶片弯角是复现期望旋流角的主要影响因素，故在设计叶片式旋流畸变发生器时，对于结构较为简单、叶片间影响较小的叶片式旋流畸变发生器的设计中主要选取合适的叶片弯角，调整叶片稠度来实现期望的旋流角。在结构复杂，叶片密集的叶片式旋流畸变发生器的设计中，可局部调整安装角角度，以获得期望的旋流角度。

4)本文仅仅研究了旋流角随安装角增量、畸变发生器外径尺寸以及马赫数的变化而变化的趋势，并且仅研究了一种叶型进行研究，所归纳的拟合公式仅适用于本文所采用的CDA叶型，但基于此拟合公式以及本文叶型可设计绝大多数的旋流畸变网，若更换其他叶型，则本文拟合公式的适用性会变差。