有源相控阵雷达均衡技术研究与实现

张小龙，朱枫，夏德平，杨斌

(1.南京电子技术研究所，江苏 南京 210039；2.东南大学毫米波国家重点实验室，江苏 南京 210096)

0 引言

现代电子战争正面临快速变化的复杂电磁环境，多种军民事应用对雷达提出了高分辨率、抗干扰、目标成像和型号识别等要求[1]。传统窄带有源相控阵雷达难以完成上述功能，采用宽带信号的雷达逐渐成为一种选择。

相控阵雷达中众多阵列天线单元及数字收发组件的各种模拟器件是引起各通道间幅相不一致的主要因素，对于窄带信号可近似认为通道产生的误差与频率无关，校准时仅需在中心频点进行校正。然而宽带雷达各通道间的幅相特性随频率变化较大，包括通道带内及通道间的频率特性不一致，这种不一致常称为通道失配[2]。通道失配将会影响数字波束形成(Digital Beam Forming，DBF)副瓣电平[3]、旁瓣相消对消比[4]及阵列输出信号信干噪比[5]等阵列处理的性能，通常在各通道中插入权系数可配置的有限冲激响应(Finite Impulse Response，FIR)滤波器来补偿通道失配，通道均衡的目的即计算各均衡滤波器的系数。

根据计算均衡器系数方法的不同可将均衡算法分为时域[6]和频域[7]两大类，文献[2]证明了这两类方法是等效的，并且提出了均衡评价准则。均衡算法的研究主要围绕以下几点进行：第一，随着通道误差的增大，提升均衡滤波器的阶数可能会出现病态矩阵，文献[8-9]提出了对角加载法，但加载量难以确定，文献[10]提出用正则化方法来解决矩阵病态的问题，并分析了正则化方法的应用条件，文献[11]提出利用奇异值分解的办法提高校正的稳定性，但都以硬件复杂度的提高和牺牲实时性为代价；第二，信号带宽较宽及高次畸变时的均衡效果不理想，对此文献[12-13]提出了带宽分割进行分段均衡的方法，但带宽分割数量难以确定；第三，针对带外误差控制，文献[7]及[14]提出频域加权均衡算法，文献[15]提出采用参考通道的幅度响应作为加权矩阵的对角元素，文献[16-18]都对带外误差进行各种形式的扩展，以降低对均衡效果的影响。此外，现有研究大多以特定的仿真模型及失配通道为基础，对算法的改进进行验证，鲜有实测宽带数据作为支撑[19]，仅文献[20-21]录取了5 MHz 及200 MHz 带宽的实测数据，但仅用剩余失配特性来评价均衡效果不够完善。本文构建了结合剩余失配特性、脉冲压缩及波束形成方向图的综合均衡评价体系，在某机载有源相控阵雷达平台上，实验验证了150 MHz 带宽信号的频域加权均衡算法，并提出新的矩形窗加权矩阵，仿真及实测数据验证了该加权矩阵的有效性。

1 均衡原理及效果评价

1.1 均衡原理

本文以接收通道均衡为例，介绍频域均衡原理，通道均衡结构示意如图1 所示。

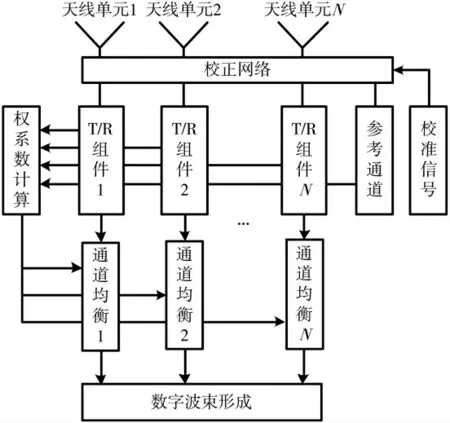
图1 通道均衡结构示意图

该有源相控阵系统由L 个天线单元和数字收发组件组成，校准信号经校正网络依次馈入接收通道，经数字组件采样下变频至基带信号，通过光纤送入数据处理进行权系数计算，后将均衡器权系数加载至接收通道中，均衡后的数字信号送至数字波束形成进行合成及后续处理。

设N 个待均衡通道的频率响应为Ci(ω)，ω 为角频率，均衡滤波器的频响为Hi(ω)，则均衡后各通道的等效频响为：

其中，i=1，2，…，N 为通道序号，下同。令所有通道均衡后的频响都等于一个参考通道的等效频响，这样可实现所有失配通道的均衡：

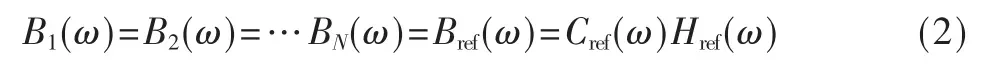
其中，Bref(ω)为参考通道的均衡后频响，Cref(ω)为参考通道的频响，可以是一个理想通道，或者是待均衡的通道之一，Href(ω)可理解为参考通道的均衡器频响，使参考通道与各通道均衡后的时延一致，参考通道的均衡器频响为：

式中，L 为滤波器阶数，(L-1)Ts/2 为滤波器时延，结合式(1)、式(2)可计算各通道均衡器频响为：

为得到均衡器频响Hi(ω)，首先需要得到待均衡通道的频响Ci(ω)，实际均衡时将同一校准信号空馈至各通道中进行测量，由于输入信号一致，则Cref(ω)/Ci(ω)等效为参考通道及待均衡通道输出信号的离散傅里叶变换之比，将式(4)取M 点快速傅里叶变换(Fast Fourier Transform，FFT)如下：

其中，m=0，1，…，M-1 为FFT 变换后的序号，下同。利用L 阶FIR 滤波器Ei(m)来拟合均衡器Hi(m)，做M 点FFT 离散化后的频响为：

式中，A 为M×L 维矩阵，称为频率因子，仅与滤波器阶数L 及FFT 点数M 有关，因此最佳均衡器的系数矢量hi可由最小化如下函数得到：

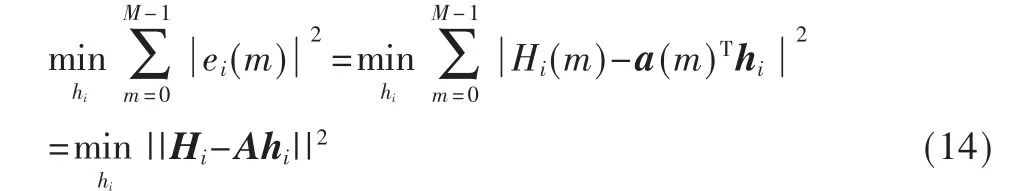
上式为经典最小二乘拟合问题，其解如下：

式中，[·]H为共轭转置。为降低带外信号误差对均衡效果的影响，可定义一个窗函数对不同频率点的误差进行加权，设加权向量为W(m)，式(14)变为：

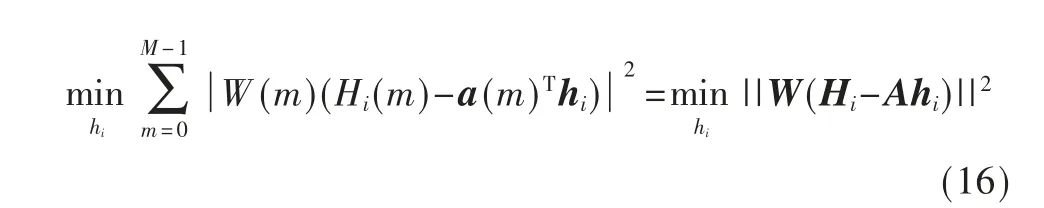
其中，W 是元素为W(m)的对角矩阵，最优解为：

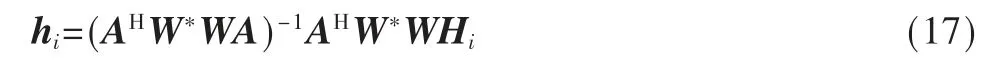
式中，[·]*为共轭。加权矩阵对角元素常用的有切比雪夫权、汉明窗权或参考通道的幅度响应[15]，然而汉明窗等常用函数带内衰减过快，对带内误差控制有损失，参考通道幅度加权对带外抑制不够深入，因此本文提出一种针对工作带宽的矩形窗加权矩阵，进一步削弱带外信号误差对拟合结果的影响，让误差函数最大程度地反映滤波器逼近程度。由式(16)可知，矩形窗仅对频域误差函数进行加权，并不对原始信号做任何处理，因而不会对均衡后的副瓣电平产生影响。本文将对这三种加权矩阵及基本算法分别进行通道均衡性能分析。

1.2 均衡效果评价

令待均衡通道的频响Ci(ω)与参考通道的频响Cref(ω)的比值为该通道的失配特性，表征该通道偏离参考通道的程度，定义如下：

其中，αi(ω)表示第i 个通道的幅度失配，用其均值与均方根△αi来描述，φiω表示第i个通道的相位失配，同样用其均值与均方根△φi来表示。

同理将均衡后的综合通道频响与参考通道频响的比值定义为剩余失配特性，表征均衡后该通道与参考通道之间的剩余特性差异，其定义如下：

其中，βi(ω)表示第i 个通道的剩余幅度失配，用其均值与均方根△βi描述，θi(ω)表示第i个通道的剩余相位失配，同样用其均值与均方根△θi来表示。

上述指标仅用来评价待均衡通道与参考通道的匹配程度，通道间的幅相一致性也可通过更直观的波束形成方向图来描述，此外为检验通道带内幅相特性，应考虑其脉压结果，避免选择实际通道作为参考通道进行均衡，导致虽然剩余失配指标很好但信号质量一般的情况，因此本文构建结合剩余失配特性、脉压及波束形成方向图的综合评价体系，可更加全面地评价均衡效果。

2 仿真模型

常用的失配模型有零极点扰动模型[6]及权系数扰动FIR 滤波器模型[3]，本文采用后者来模拟失配通道，仿真参数如下：校准信号为线性调频信号，带宽为150 MHz，采样率为200 MHz，幅度失配均方根为0.05，相位失配均方根为0.05 rad，参考通道选择理想通道，共仿真8 个通道，其中前4 个通道的失配特性如图2 所示。

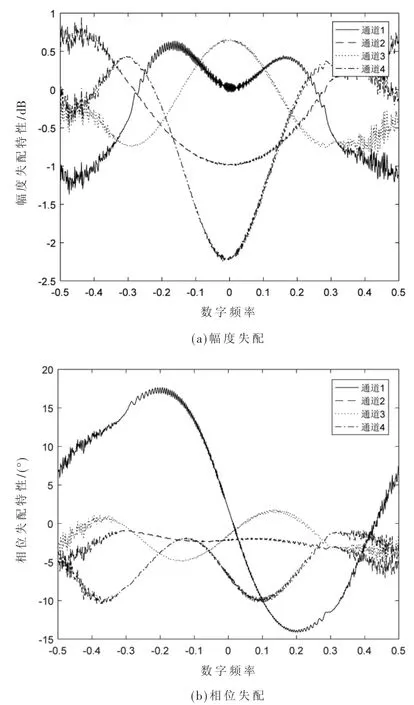
图2 仿真通道失配特性

由图2 可知，幅度失配在3.5 dB 左右，相位失配在30°左右。依次采用基本算法、参考通道幅度权、汉明窗权及本文新提出的矩形窗权对各通道进行通道均衡，其中前4 个通道矩形窗加权均衡后的剩余失配特性如图3所示。

由图3 可知，均衡后各通道幅相特性基本一致，均衡后的剩余幅度失配均值接近0 dB，剩余相位失配均值接近0°，剩余幅度失配均方根△βi及相位失配均方根△θi如图4 所示。

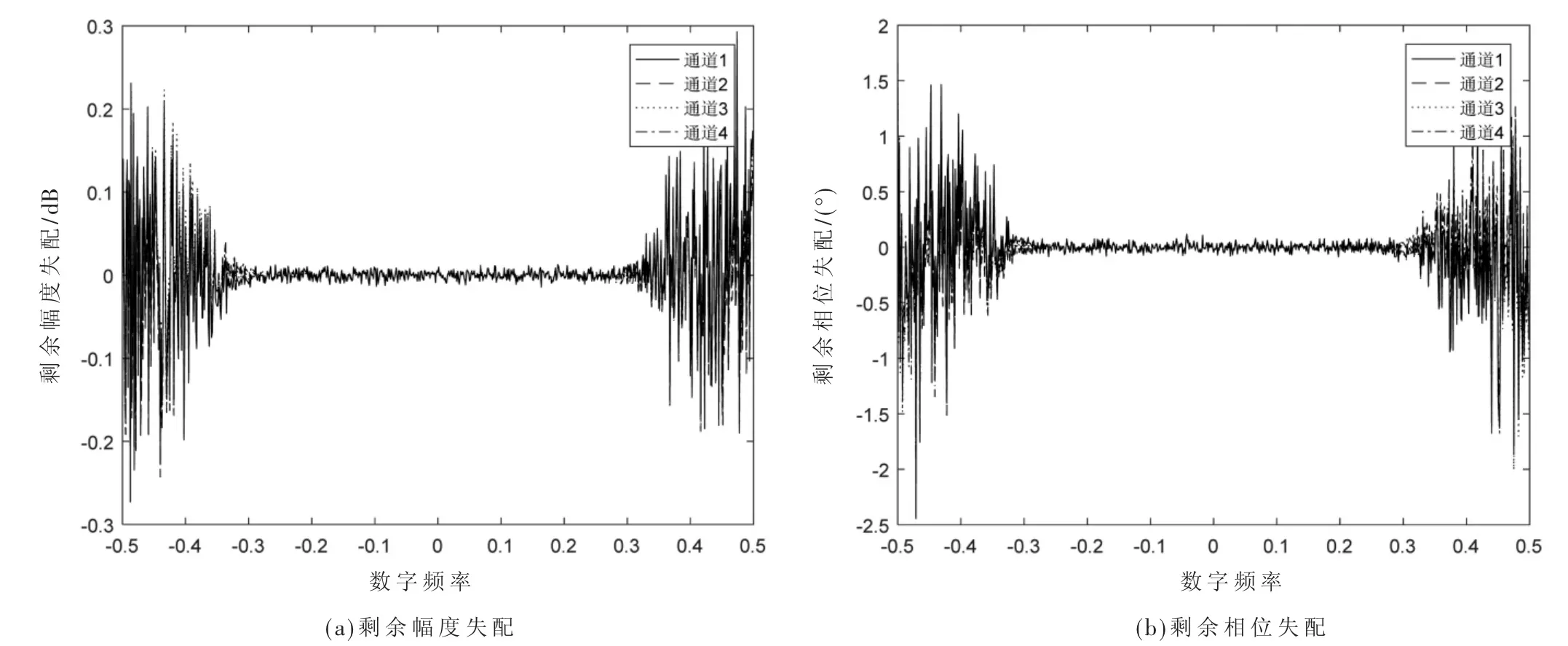
图3 仿真通道均衡后剩余失配幅相特性

从图4 可以初步看出矩形窗加权均衡效果最优，为定量分析将剩余失配特性在通道上求均值后整理如表1 所示。

由表1 可知，矩形窗加权均衡算法性能最优，剩余幅度失配均方根较现有算法提升了约7 dB，剩余相位失配均方根较现有算法提升了约0.05°。

表1 仿真通道四种均衡算法的剩余失配特性

均衡前的脉压结果如图5 所示，由于仿真失配通道差异不大，均衡前后脉压主副瓣比都能达到-40 dB 以上。

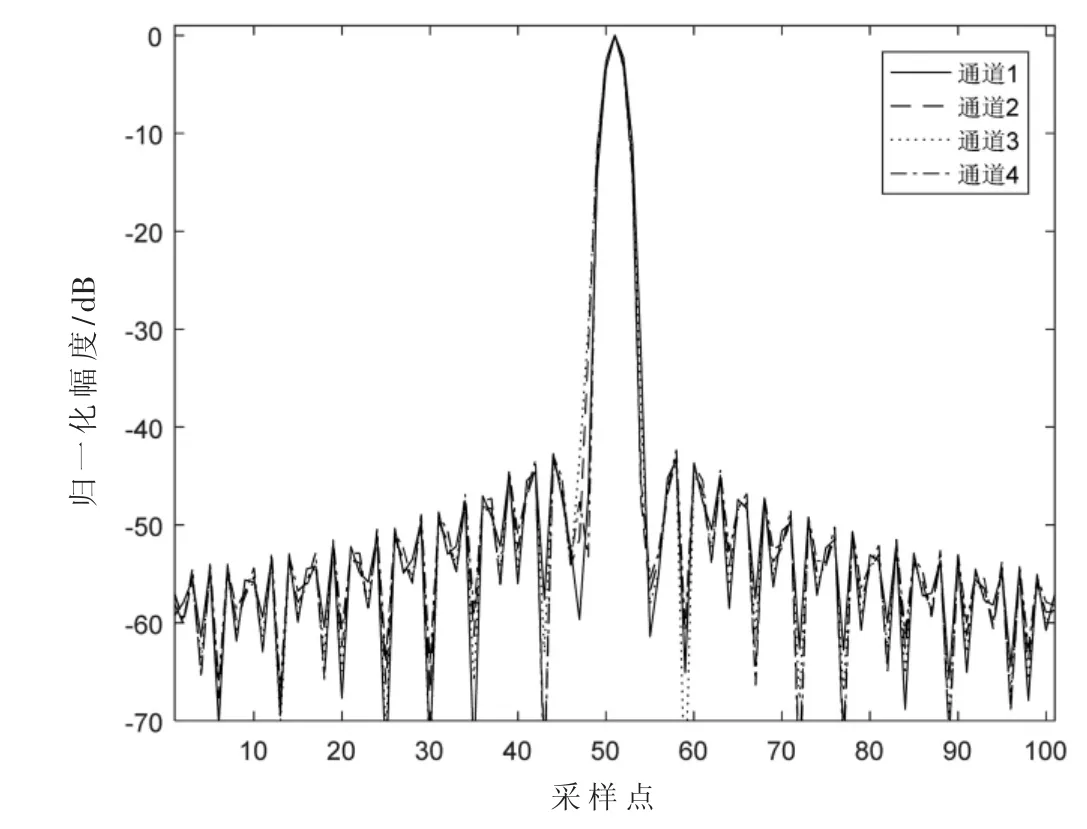
图5 仿真通道均衡前脉压结果

将中心频点均衡前后及理论波束形成方向图如图6所示，由于仿真失配通道差异不大，均衡前方向图较理论方向图仅副瓣略微抬高，均衡后与理论一致。

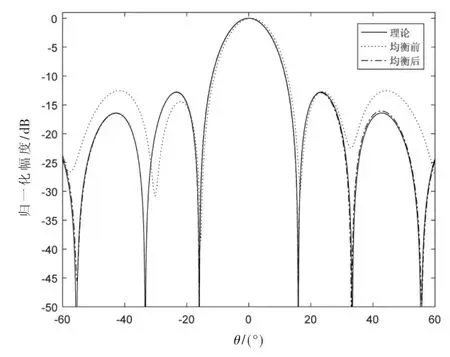
图6 仿真通道均衡后波束形成中心频点方向图

3 实测数据

从仿真通道均衡前后脉压结果及波束形成方向图可知，仿真模型带来的通道失配差异有限，利用实测数据进行算法验证很有必要。本文以某机载有源相控阵雷达为平台，均衡校准信号采用线性调频信号，信号带宽为150 MHz，脉宽为4 μs，采样率为200 MHz，首先给出以理想通道为参考通道的幅相失配特性，如图7 所示。

同样仅对前4 个通道的失配特性作图，从图7 可知，实际通道的失配特性要比仿真通道大得多，其幅度失配在30 dB 左右，相位失配在200°左右，且所有通道带内一致性都不平坦，应选择理想通道作为均衡参考通道，同时也体现了将脉压结果纳入均衡评价指标的必要性。采用基本算法、参考通道幅度权、汉明窗权及矩形窗权进行通道均衡效果对比，其中矩形窗加权均衡后的剩余失配特性如图8 所示。

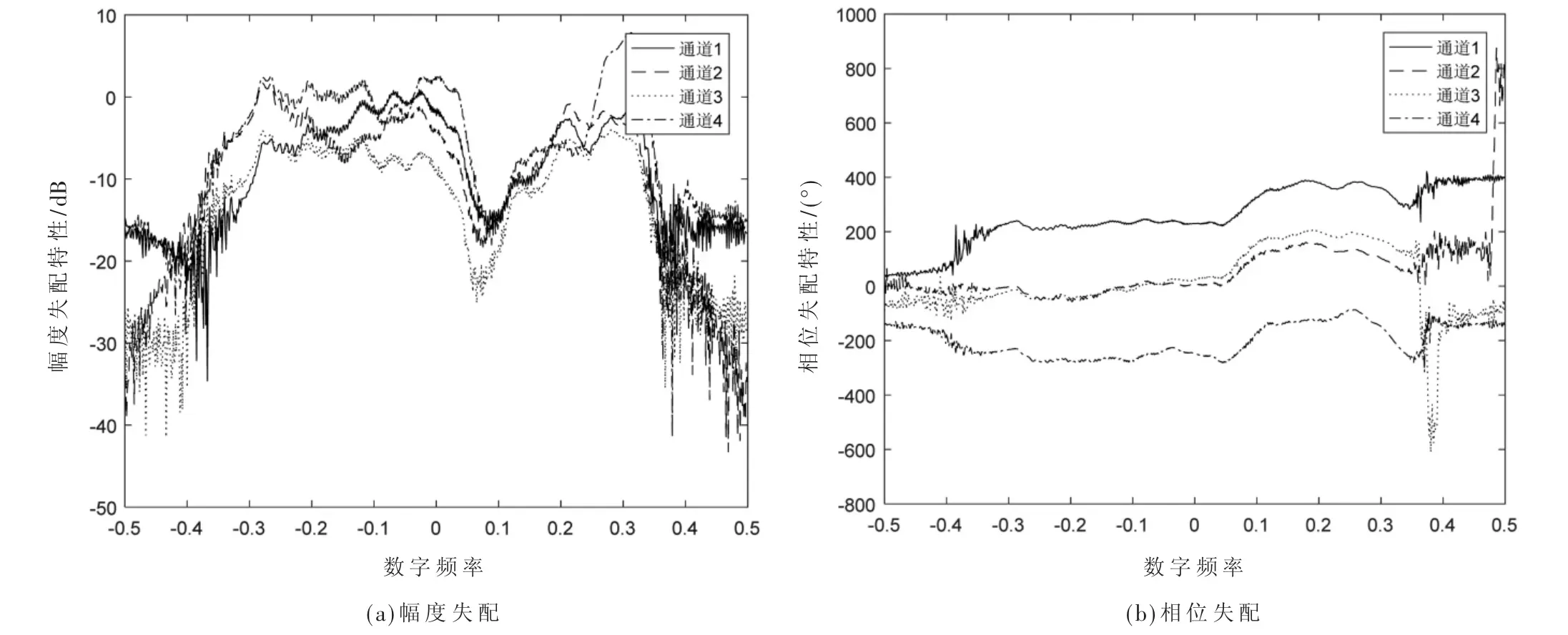
图7 实际通道失配特性

图8 实际通道均衡后剩余失配幅相特性

均衡后的剩余幅度失配均值接近0 dB，剩余相位失配均值接近0°，剩余幅度失配均方根及相位失配均方根如图9 所示。

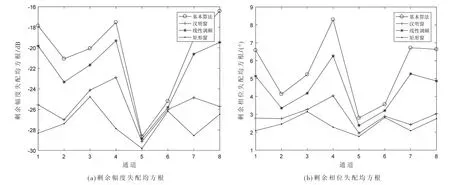
图9 实际通道均衡后剩余失配均方根

同样将剩余失配特性在通道上求得均值后整理如表2 所示。

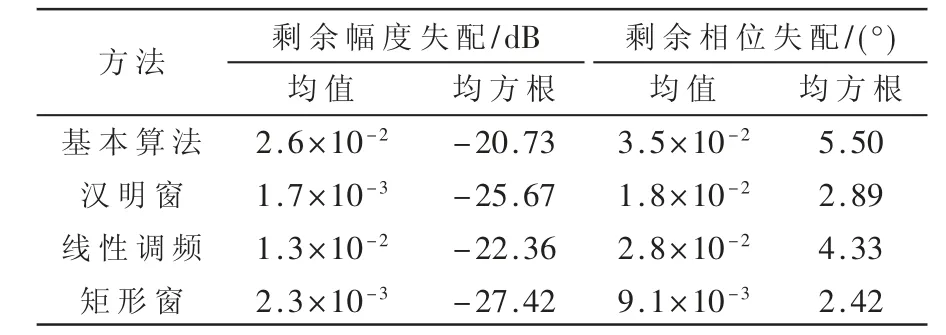
表2 实际通道四种均衡算法的剩余失配特性

由表2 可知，矩形窗加权均衡算法性能最优，剩余幅度失配均方根较现有算法提升了约2 dB，剩余相位失配均方根较现有算法提升了约0.4°。

均衡前后的脉压结果如图10 所示，由于实际通道带内一致性不够平坦，导致脉压结果不理想，若此时仍选择实际通道作为参考通道，则均衡后的脉压结果将逼近于该实际参考通道，尽管均衡后的剩余失配特性指标满足要求，但最终的脉压结果显然对后续信号处理是不利的。在选择理想通道为参考通道进行均衡后，脉压主副瓣比可达到-40 dB 以上，与理论脉压结果相当。

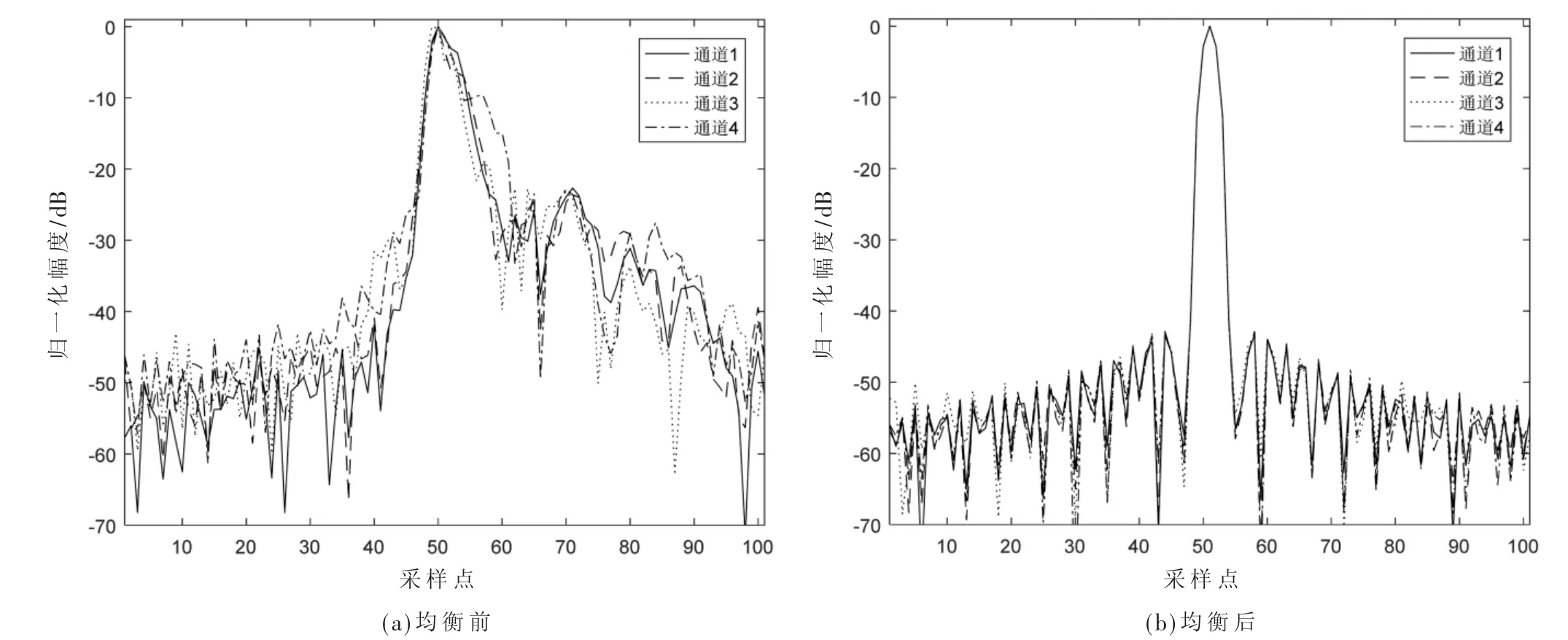
图10 实际通道均衡前后脉压结果

均衡前后的波束合成方向图如图11 所示。由于实际通道幅相失配特性过大，导致均衡前未形成主瓣，均衡后的方向图如图11(b)所示，其在全带宽上形成了与理论接近的方向图。

图11 实际通道均衡前后波束形成方向图

4 结论

本文构建了结合剩余失配特性、脉压及波束形成方向图的综合评价体系，可更加全面地评价均衡效果，以某机载有源相控阵雷达平台为基础，工程实验了频域通道均衡，并对新提出的矩形窗加权均衡与现有算法进行比较，仿真结果及实测数据都表明新算法对均衡性能有一定的提升，为通道均衡提供了新思路。