基于UCC1895 移相全桥电源的设计

林杰，马文超

(中国电子科技集团公司第五十八研究所，江苏 无锡 214035)

0 引言

随着开关电源对功率密度的要求越来越高，提高开关频率，减小磁性器件的体积和重量成为一条最重要的途径。但是伴随着开关频率地逐步提高，一方面，功率管硬开关带来的开关损耗会导致器件的发热严重，从而迫使工程师增加散热器件的面积；另一方面，硬开关还会导致功率管在开关过程中承受更大的电压应力，同时还会产生高频振荡，这会加剧电磁噪声的问题[1]，工程中通常会使用更多的滤波电感和电容来应对[2]，导致电源体积和重量增大，这严重制约了开关电源高频化的发展[3-4]。

为了解决这些问题，软开关技术应运而生。移相全桥就是其中一种可以实现零电压开关的软开关拓扑，相比于其他软开关拓扑，移相全桥具有功率等级高，输入输出隔离等优势。

1 移相全桥电路工作原理分析

1.1 移相全桥电路结构

移相全桥电路的基本结构和主要工作波形如图1和图2 所示，其中Q1～Q4为四个主功率开关管；D1～D4分别 是Q1～Q4的体二极管；C1～C4分别是Q1～Q4的寄生电容或外部并联的电容；Ls是谐振电感，它可以是变压器的漏感或外接的电感，也可以是两者之和；Tr 为主功率变压器；DR1和DR2是两个整流二极管，构成了全波整流电路；Lout和Cout分别是输出滤波电感和滤波电容[5]。

图1 移相全桥基本结构

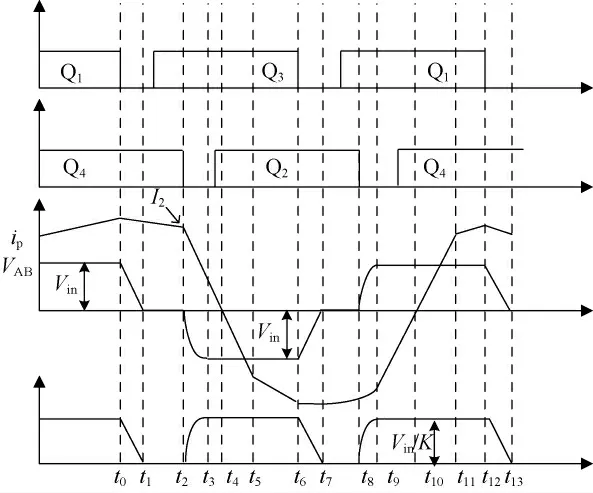
图2 移相全桥主要工作波形

所谓移相是指每个桥臂的上下两个功率管都是180°互补导通，而斜对角的两个功率管的驱动信号之间存在一个相位差，即移相角。移相角越小，斜对角驱动信号的重叠部分越多，变压器原边的等效电压越高，输出电压越高。一般地，Q1和Q3的驱动信号分别超前于Q4和Q2，因此Q1和Q3组成的桥臂被称为超前桥臂，Q2和Q4组成的桥臂为滞后桥臂。

1.2 功率管软开关的实现

下面来分析其零电压关断和零电压开通的实现过程。当Q1和Q4关断时，由于Q1和Q4的等效电容和外接电容的存在，Q1和Q4的DS 两端电压VDS从零开始上升，且上升速率被限制，因此，可以认为Q1和Q4是零电压关断。

由于原边电流的作用，C1和C4会被充电至Vin，而C2和C3会被放电至零，因此Q2和Q3的体二极管D2和D3会导通，即Q2和Q3的DS 电压VDS为体二极管导通压降，可以近似为零，此时开通Q2和Q3，就可以实现Q2和Q3零电压开通。

由上面的分析可知，为了实现功率管的零电压开通，需要利用原边电流来给功率管的等效电容充放电，并且考虑到变压器存在的寄生电容，也就是说原边的能量必须满足如下条件：

其中，Clead是超前桥臂MOS 管的等效电容，Clag是滞后桥臂MOS 管的等效电容，CTR是变压器的寄生电容。

具体来看，超前桥臂的零电压开通要比滞后桥臂的零电压开通更容易实现，这是因为在超前桥臂的开关过程中，输出滤波电感Lout和谐振电感Ls是串联关系，而且一般情况下Lout的值都比较大。所以，原边电流ip近似认为不变，是一个恒流源，可以很容易地对超前桥臂功率管和变压器的等效电容进行充放电。

而滞后桥臂的零电压开通实现之所以困难，是因为在滞后桥臂的开关过程中，副边的两个整流二极管DR1和DR2都处于导通状态，变压器副边被短路，输出电感上的能量仅在副边通过二极管续流，和原边脱离了关系。所以，仅仅只有谐振电感里的能量能够对滞后桥臂的功率管和变压器的等效电容进行充放电。所以，谐振电感中的能量需要满足式（2）：

一般情况下，谐振电感相比于输出电感折算到原边的感量要小得多，所以相对于超前桥臂来说，滞后桥臂的零电压开通要更困难。

2 移相全桥主电路设计实现

2.1 主要参数规格

本文以300 W 移相全桥电源为例来说明移相全桥主电路的设计方法和计算过程。具体规格如表1 所示。

表1 300 W 移相全桥具体参数规格

2.2 关键器件参数计算

2.2.1 主功率变压器

在隔离型DC-DC 开关电源的设计中，变压器一般都起到了功率传输和原副边隔离的作用。而变压器设计的好坏关系到系统能否正常工作，并且对整机效率影响很大[6]。

在移相全桥变压器的设计中，首先计算变压器的匝比，需要注意，移相全桥拓扑的最大占空比出现在输入电压最低时，且考虑到副边占空比存在丢失的情况并保证留有足够的裕量，取最大占空比Dmax为0.7。另外，取整流二极管导通压降Vf为0.5 V。则变压器匝比的计算如式（3）所示。

其中Vinmin=200 V，则n=4.9，在这里取整，取匝比为5。

考虑到功率等级和开关频率，初步选定磁芯为PQ3535，其Ae=196 mm2，取Bmax=0.1 T，则副边匝数可由式（4）得出[7]:

其中Vout为28 V，可以取Ns为4，因为变压器匝比为5，则原边匝数Np为20。

在计算高频变压器的绕组导线线径时，需要考虑到集肤效应，一般要求导线线径要小于2 倍的集肤深度，在开关频率为100 kHz 时，集肤深度可由式（5）得出：

因此导线线径应小于2 倍的Δ 即0.484 mm。

而变压器原副边最大的电流分别为：

考虑到散热方式为空气自然对流，因此取电流密度J 为3.5 A/mm2，原边可以选用直径为0.1 mm 的漆包线，则原边股数为：

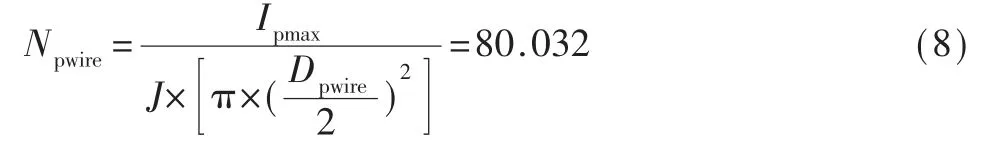
副边选用直径为0.2 mm 的线，则副边股数为：

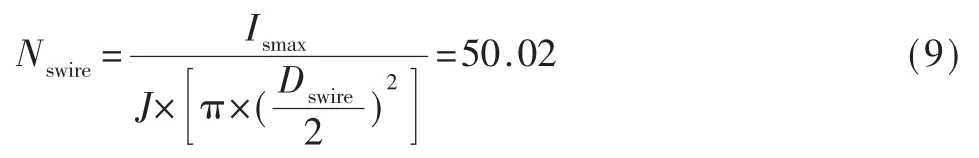
那么，最终变压器的原边线径为0.1 mm×80 股，副边线径为0.2 mm×50 股。

2.2.2 输出电感

将电感电流纹波设定在20%，则输出电感的计算公式如式（10）所示：

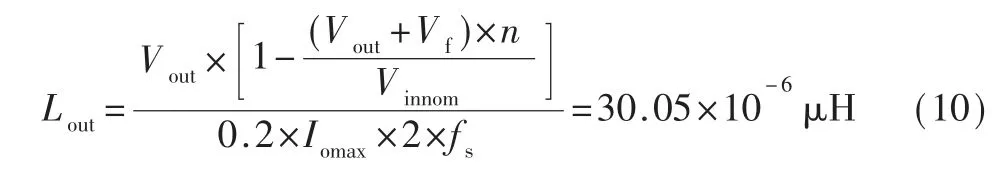
其中Vinnom=270 V。电感电流的最大值为：

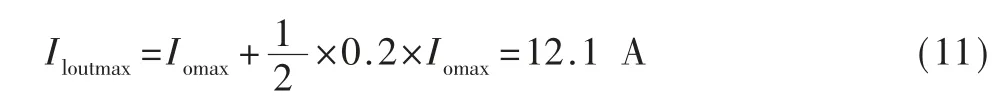
考虑到输出电感的电流是单向流动的，存在很大的直流分量，在直流偏磁的作用下，感量会存在衰减，因此最终选定的电感为PA4349.473ANLT，其额定感量为47 μH，额定电流为17 A，在直流电流为11 A 时，感量衰减为35 μH 左右，符合设计要求。

2.2.3 主功率开关管

已知最大输入电压为330 V，考虑到1.5～2 倍的裕量，选用耐压为600 V 的功率管，又因为开关频率为100 kHz，不太适合选用IGBT。且最大输出电流为11 A，假设存在20%的峰峰值电流纹波，则副边的电流最大值为12.1 A，折算到原边，电流最大值为2.42 A。考虑到自然风冷的设计效果，需要选用Rdson较小的MOSFET，最终选择的MOS 管为IPB60R125CFD7,其耐压为600 V，最大漏极电流为18 A，Rdson为125 mΩ。

2.2.4 输出整流二极管

由于本设计开关频率较高，且输出电压不高，因此可以选择肖特基二极管作为输出整流二极管，二极管承受的最高反向电压和额定电流分别可由式（12）和式（13）得出：

考虑到裕量和温升，最终选用的输出二极管是STTH16R04CG，其耐压是400 V，额定电流是20 A，每一路采用两颗并联均流散热。

3 基于UCC1895 的隔离驱动设计

本文的移相全桥电源主控芯片采用的是TI 的UCC1895，该芯片为一款移相PWM 全桥控制器。芯片输出四路驱动信号，用于控制全桥电路中四个功率管的导通和关断，以得到不同输出电压。其可工作于电压或电流模式，具有零电压开关、可编程死区设置和自适应延时等特性。

但UCC1895 的四路驱动信号驱动能力很弱，需要外加电路才能够驱动大功率MOS 管，且还要考虑同一桥臂驱动的隔离。所以，本文针对UCC1895 的应用，采用了如图3 所示的驱动电路。其中，ABCD 为UCC1895 的四路驱动信号，JS614 为一款低边单路驱动器，最大峰值驱动电流可达14 A。可以直接用一颗JS614 来驱动下管，然后再用一颗JS614 配合隔离变压器来驱动上管，实现同一桥臂上下管的驱动隔离。

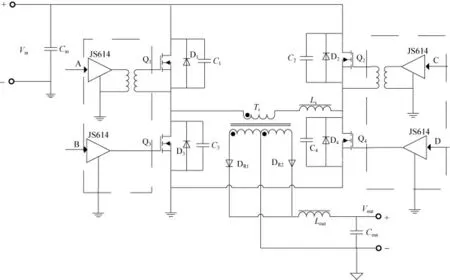
图3 基于UCC1895 的驱动设计

4 仿真分析

为了验证器件参数和方案的可行性，按照表1 所示的设计规格和计算参数，在SIMetrix 中搭建了仿真模型，图4 为系统闭环且满载输出时的桥臂中电压和谐振电感电流波形，可以看出仿真波形和理论分析一致。

图4 桥臂中点电压和谐振电感电流

图5 为零电压开通的实现波形，在图中圈出的部分可以明显看出，MOS 管的DS 电压VDS在驱动信号VGS到来之前已经到零了，所以是完全的零电压开通。

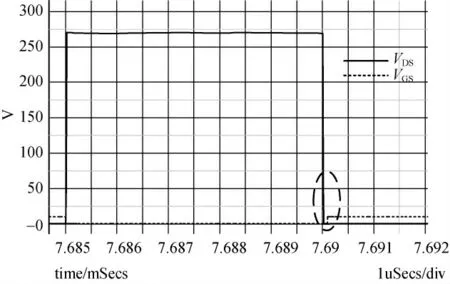
图5 零电压开通的实现波形

图6 为在满载起机时的输出电压和输出电流的波形，可以看出系统在4 ms 后进入稳态，输出电压为28 V，输出电流为11 A。

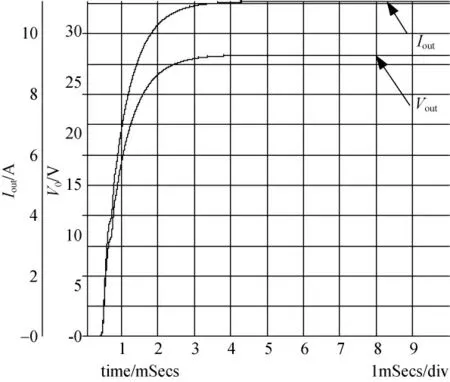
图6 闭环时输出电压和输出电流

从以上仿真结果可以看出，对于关键器件的参数计算是合理的，而且基于JS614 和隔离变压器的驱动方案是可行的。

5 样机实验验证

在仿真的基础上进一步研制了300 W 移相全桥样机，具体规格指标如表1 所示。抓取了关键波形，并对实验结果进行了分析。

图7 是实测的零电压关断波形，和理论分析一致，由于MOS 管的寄生电容以及外界电容的存在，MOS 管在关断时，MOS 管的DS 电压VDS在驱动信号VGS撤去之后才开始上升，实现了零电压关断。

图7 零电压关断波形

图8 为超前桥臂零电压开通波形，在驱动信号到来之前，MOS 的DS 电压VDS提前下降为零，实现了零电压开通。

图8 超前桥臂零电压开通波形

图9 为滞后桥臂零电压开通波形。可以看出，在相同的负载条件下，滞后桥臂和超前桥臂相比，零电压开通的实现要困难一些。

图9 滞后桥臂零电压开通波形

图10 是输出电压为28 V，输出电流为5.5 A 时的半载带载启机波形。

图10 半载起机波形

输出电压有轻微的超调，约2.6 V，但是在控制器的作用下很快调节回来，证明了系统的动态性能。

图11 是输入电压为270 V 时的整机效率，由于实现了零电压关断和零电压开通，减小了开关损耗，使得峰值效率能够达到94%。

图11 输入电压为270 V 时的整机效率

6 结论

移相全桥凭借其软开关、功率等级高的优势，在中大功率高频应用场合下占据了重要地位，能够满足服务器等电源对于高功率密度和高效率的要求。本文对移相全桥的原理和设计过程进行了分析。提出了UCC1895 配合低边单路驱动器以及隔离变压器的系统方案，并利用仿真和硬件实验结合的方式进行了验证。