浅谈对数学探究性学习的思考

周 斌

（江苏省南京市江宁高级中学，211100）

在当前的教育背景下，更加提倡充分发挥学生在学习活动中的积极性与主动性，强调学生学习方式的转变.基于这一要求，探究性学习模式的应用价值逐渐突显出来.本文将结合教学实践活动，对如何在高中数学教学中组织开展有效的探究性学习进行探索.

一、数学探究性学习的主要困惑

1.兴趣与成绩矛盾突出

尽管很多教师已经意识到探究性学习的重要性，但是在高中阶段的教学中，高考仍然是学生面临的一个重要任务，所以提高学生成绩是家长和学校十分关注的问题.为了提高学生的学习成绩，教师普遍会直接将现成的知识传授给学生.通过这种教学方式中，学生表面上掌握了许多知识，但并没有了解知识内部的本质特征.同时，这种学习方式也会逐渐使学生丧失对数学知识的好奇心以及在数学学习中的创造力.

2.教学时间十分紧迫

在探究性学习中，一个十分突出的特点就是注重过程，探究性学习过程是需要一定的时间投入的.但是，由于课程安排比较紧凑，再加上课堂教学的时间是相对固定的，所以如何合理安排教学时间是教师应该着重思考的问题.

3.全员参与难度较大

在高中阶段的教学中，班级的规模通常较大.由于学生在成长与发展的过程中普遍存在一定的差异，所以导致班级中学生的个性与能力会出现比较明显的分化现象.因此，教师需要思考如何对学生之间的差异进行协调.

二、数学探究性学习的组织策略

1.基于问题导学的探究性学习

探究性学习的实施，一个十分重要的目的就是为了改变学生直接接受现成知识的学习方式.基于这一目的，问题导学的方式无疑具有十分重要的作用.在问题导学中，教师需要将问题作为知识内容的载体，并通过启发和引导的方式促使学生解决问题，从而达到促进学生转变学习方式的目的.因此，在组织教学活动时，教师应对教材内容进行深入的研究，并结合重点知识提出一些具体的问题，要求学生思考.这样一来，可以充分发挥出学生的主观能动性，从而促进学生的知识理解.

以“函数零点的存在性定理”的相关知识为例.为了引导学生对相关知识进行有效的探究活动，可利用问题对学生进行点拨.首先，让学生准备一条细线和一支笔芯，将笔芯放在桌子上保持不动，将其当作轴.然后，把活动的细线作为函数图象，细线两端分别为A、B两点，观察笔芯和细线的交点个数，并思考以下问题：（1）当A、B两点在笔芯的两侧时，细线和笔芯所在直线会有几个交点？交点会在什么位置？（2）当A、B两点在笔芯同侧时，细线和笔芯所在直线会有几个交点？（3）在什么情况下，细线与笔芯所在直线一定会存在交点？（4）根据函数零点的概念，怎样用数学语言表达以上结论？接着，学生根据这些问题进行自主探索.引导学生根据自己的理解，相互之间进行交流与讨论.在不同观点的交流与碰撞中，学生逐渐对本节课的相关知识形成了比较准确的认识.

2.基于变式引申的探究性学习

所谓变式，主要是指在教学活动中有计划、有目的地对命题进行合理的变化.当然，这种变化通常是对问题非本质条件的改变，其目的就是为了引导学生对事物的本质特征进行更加准确的理解.

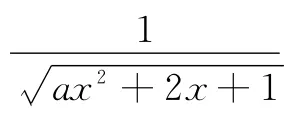
变式1：如果函数y=log2（ax2+2x+1）的定义域是R，那么实数a的取值范围是什么？

变式2：如果函数y=log2（ax2+2x+1）的值域是R，那么实数a的取值范围是什么？

让学生根据自己实际水平选择不同的角度进行解题练习.最终，通过这种方式，有效地突破了教材知识的局限性，使学生在理解和掌握基础知识的前提下，举一反三，从而帮助学生对数学对象的本质特征有更加深入的理解.

3.基于特殊一般的探究性学习

从特殊研究对象中抽象出一般规律，这是数学学习中一种至关重要的研究方法.这种研究方法的一个主要特征就是从个别事物的特殊现象过渡到较大范围的一般规律.为此，教师应该给学生提供更加恰当的学习材料.毋庸置疑，这种探究方式不但有利于促进学生对数学规律的理解与掌握，而且能够在一定程度上促进学生抽象思维能力的发展.

比如这样一个问题：有一幅壁画，最高点A到地面的垂直高度是4m，最低点B到地面的垂直高度是2m，如果从距离地面1.5m的C点位置欣赏这幅画，那么当C点距离墙面的距离是多远时，可以使得观看壁画上下两端的视角θ最大？根据这个问题，教师可设计一道改编题：在寒假期间，小红去参观一个画展，为了保护作品，在画的前方用垂直于地面的玻璃墙将画与观众隔开，画的最低点到地面的距离是1m，玻璃墙和画之间的距离是1 m，如果小红的身高是αm（0＜α＜3），此时她站在离画xm的位置观看欣赏画作.请问x取何值时，可以使小红观看作品上下两端的视角θ最大？从解题思路来看，需要将小红的身高分为1＜α＜3，α=1，0＜α＜1这几种不同的情况讨论，然后通过两角和、差的正切公式列出tanθ的表达式，最后通过函数单调性的分析，计算出θ的最大值.不难发现，尽管两个问题均是数字计算，但问题中的思维张力却是不同的.经过改编之后的探究材料，更加贴近实际生活情境，所以学生在问题探究中的感悟也更加深刻.由此可见，利用恰当的材料，引导学生抽象和归纳一般性的解题思路，对于学生的数学学习具有十分重要的促进作用.

4.基于活动实践的探究性学习

在当前的数学教学中，一个较为明显的现象，就是学生对数学知识难以产生浓厚的学习热情.一个主要原因就是数学内容的呈现方式比较枯燥.为了改变这种情况，教师可以组织学生进行一些实践性的练习活动.这样一来，不但可以使学生在实际问题的解决中对所学知识有更加灵活的应用，而且可以突破课堂的局限性，使学生的学习活动更加多样化，从而有效激发学生的学习热情.

以“数列”的相关知识为例，教师组织学生探究了这样一个生活问题：按揭贷款是当前比较普遍的一种业务，通常实行的是按月等额还本付息的方式.那么等额数是怎样得出的？如果贷款的金额是a元，贷款的月利率为p，还款方式是按月等额还本付息，假设第n个月后还款的本金是an，那么最后归还的本息数量是多少呢？再以“概率和排列”的知识为例，在彩票数字中，会从m个元素当中任意选取n（n≤m）个元素，按照这种排列顺序进行排列，怎样可以增加中奖概率.要求学生在课后实践中，对长期以来的彩票数据进行分析.最终，利用这种方式，逐渐强化学生对其中蕴含的数学知识的理解.

总的来说，尽管在新课改深化实施以来，高中数学的探究性学习已经取得了较大的进展.但在实际的教学活动中，仍然存在一些亟待解决的问题.因此，教师应继续对课程改革的理念进行更加深入的研究，并熟练掌握不同形式的探究性学习活动组织方式.同时，教师还应该及时对教学活动中出现的新问题进行调整，以此来促进教学过程的改进与优化，从而循序渐进地促进教学质量的提升.