含参数的幂函数问题求解策略
◇ 山东 于苗苗
含有参数的幂函数问题是幂函数图象与性质应用的一类重要问题,正确求解含参数的幂函数问题关键是理解幂函数的概念、图象特征以及性质等.本文就举例分析常见的几种含参数的幂函数问题及其处理策略.
1 概念中的含参问题
判断一个函数是否为幂函数要把握住幂函数的概念.

分析本题需根据幂函数的概念建立含有相应参数的不等式组,通过求解不等式组来达到确定参数的目的.
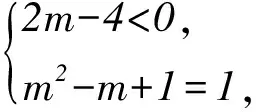

2 图象中的含参问题
根据幂函数的图象特征,关注幂函数的指数在α>1,α=1,0<α<1,α=0以及α<0时幂函数y=xα的图象特征,建立相应的关系式并结合其他相关的条件确定参数的取值情况.

分析依据幂函数的图象特征来确定解析式,需构建指数满足的不等式解出相应参数的取值范围,再进一步挖掘隐含条件合理分类确定.
解因为函数的图象与两坐标轴都没有公共点,则n2-2n-3≤0,解得-1≤n≤3,又由于n∈Z,所以n=-1,0,1,2或3,又因为函数图象关于y轴对称,则n2-2n-3为偶数,当n=-1时,n2-2n-3=0为偶数.
当n=0时,n2-2n-3=-3为奇数;当n=1时,n2-2n-3=-4为偶数;当n=2时,n2-2n-3=-3为奇数;当n=3时,n2-2n-3=0为偶数,所以n的值为-1,1或3.当n=-1或3时,幂函数的解析式为y=x0(x≠0);当n=1时,幂函数的解析式为y=x-4(x≠0).

3 性质中的含参问题
在研究幂函数的性质时,要注意幂函数的定义域,在定义域取值的限制条件下,分析对应的奇偶性与单调性等性质.

分析正确理解题目所隐含的条件m∈N+,并在此条件上对幂函数的性质加以正确分析与判断.
解由于幂函数的指数m2+m-1=m(m+1)-1,而m∈N+,从而可以判定m2+m-1是正奇数,所以幂函数y=f(x)的定义域为R.
由于幂指数m2+m-1是正奇数,则f(-x)=(-x)m2+m-1=-xm2+m-1=-f(x),所以幂函数y=f(x)是R上的奇函数,同时幂函数y=f(x)在R上单调递增.

幂函数是高中数学最基本的函数类型,也是高考必考内容之一.涉及含参数的幂函数问题,要综合幂函数的概念、图象与性质,以及函数的解析式、图象与基本性质等进行求解,这类问题能很好地考查基础知识与知识应用能力.

