轻杆模型的疑难问题研究
◇ 海南 孙云贵
轻杆是高中物理的重要模型之一,由轻杆构成的系统,无论出现在运动学还是动学力问题中往往都是难点所在,并且极易出错.本文通过对高中物理中一个常见实例的分析求解,展示与轻杆相关力学问题的分析方法、分析过程和注意事项.
1 问题的提出
轻杆是物理中重要的理想化模型之一.根据轻杆模型的定义,我们知道,它是理想化的刚体,质量为0.
大多数物理问题,往往不单独以轻杆为研究对象,而是研究轻杆及其连接的物体组成的系统,比如轻杆与质点组成的系统,用这样的系统对实际问题进行简化,是对实际问题的近似.围绕这类系统的力学问题往往很复杂,牵涉的物理、数学知识较多,计算一般比较烦琐,要综合运用物理、数学规律才能正确求解.那么,我们应该怎样分析此类问题呢?
1)对轻杆与质点结合构成的系统,不能简单地将其视为质点,而应视为刚体;
2)特别要注意的是,受力分析时,杆对物体的弹力方向通常并不沿着杆的方向,受力分析图中力的作用点要画在实际的作用点上;
3)要综合运用力学规律,特别是有关刚体的力学规律列方程(组).
下面通过案例一起感受一下以轻杆和质点等模型为情境的力学问题的分析及注意事项.
2 含轻杆模型的问题分析
2.1 含有轻杆模型的问题案例
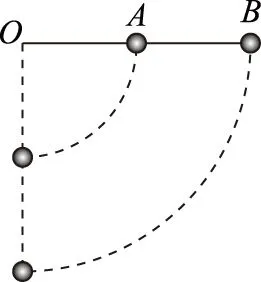
图1
案例如图1所示,长为L的直轻杆一端可绕水平光滑的转轴O在竖直平面内转动,在杆的中点A和末端B各固定一个质量分别为mA和mB的小球,重力加速度为g.将杆置于同O点在同水平面位置,将其由静止释放,在杆由水平位置转到竖直位置的过程中,求:
(1)杆分别对两个小球所做的功;
(2)杆对两小球的作用力;
(3)运动的时间.
2.2 含有轻杆模型问题案例的求解
现在,我们分三步对案例进行求解.
第一步,第(1)问比较简单,根据高中阶段知识很容易解决.取杆及两球构成的系统为研究对象,系统的机械能守恒;再计算A、B两球各自的机械能增量;最后用功能原理算出杆对A、B做的功.由于轻杆的约束,两球运动过程中每一时刻的角速度均相同.
选O所在的水平面为零势能面.A、B及轻杆构成的系统在运动过程中应用机械能守恒定律,有
(1-1)
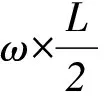
(1-2)
对A球,由功能原理有
(1-3)
式(1-3)的左边是A球机械能的增量,方括号内表示A球运动到O点正下方时的机械能,初状态的机械能为0;右边是杆对A球所做的功.由式(1-2)和式(1-3)解得
(1-4)
同理,对B球,由功能原理有
(1-5)
可求出杆对B球所做的功
(1-6)
观察式(1-4)和式(1-6),不难看出,轻杆对A做负功,对B做正功,均不为0.因而,杆对两球的作用力与它们的速度方向不可能垂直,也就是说,杆对两个小球的作用力并不沿杆的方向.
第二步,求解第(2)问,杆对A球、B球的作用力.
由第(1)问的讨论可知,杆对两球的作用力是变力,随着杆转过的角度的变化,大小和方向均随之变化.如果直接用静力学的方法去求,通常不能得出正确答案.我们可以另辟蹊径:如果能求出小球运动的加速度,就可以用牛顿第二定律求出合力,再用静力学的规律求出杆对球的作用力.小球运动的加速度可以采用这样的方法进行求解:将球的加速度分解成法向(向心)加速度an和切向加速度aτ,只要将它们分别求出来,再求矢量和,就得到合加速度.
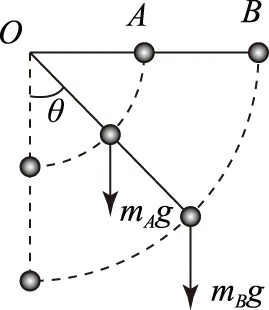
图2
系统的运动是刚体定轴转动,O为转轴,取垂直纸面向外为正方向,角度以竖直向下为始边,以逆时针为正.如图2所示,当系统由初始的水平位置转至角度θ的位置,此时,系统所受外力矩为
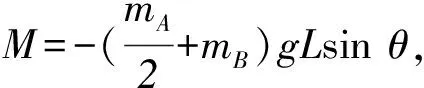
(2-1)
因而,此时杆运动的角加速度为
(2-2)
式中的I是系统对转轴O的转动惯量,其大小为
(2-3)
由切向加速度与角加速度的关系aτ=βr,可求出A、B两球此时切向加速度的大小:
(2-4)
(2-5)
由机械能守恒定律有
(2-6)
由式(2-3)及式(2-6),解得当杆与水平面之间的夹角为θ时杆转动的角速度ω为
(2-7)
式中的负号表示角速度ω的方向垂直纸面向内.再由向心加速度an=ω2r可分别求出A、B两球的向心加速度大小为
(2-8)
(2-9)
下面,我们可以运用牛顿第二定律求出两个小球在杆从水平位置转动θ角时,轻杆对它们的作用力的大小和方向.
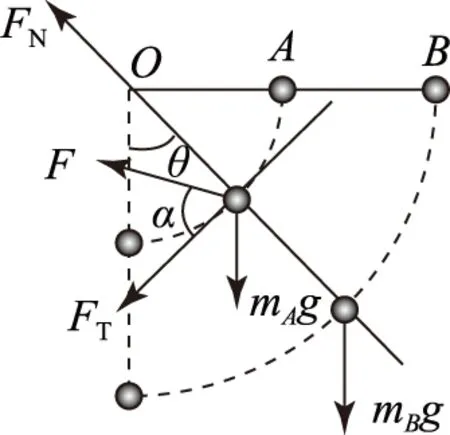
图3
对A球进行受力分析,如图3所示,图中的F是杆在系统转过角度为θ时对A球的作用力.由于F的方向未知,不妨先假设它沿图中所示的方向,真实方向由后面的计算确定.以指向O的方向为n轴,以A运动的切线方向为τ轴建立直角坐标系.F与τ轴的夹角为α.分别沿指向O的方向及球运动的速度方向,由牛顿第二定律有
Fsinα-mAgcosθ=mAanA,
(2-10)
Fcosα+mAgsinθ=mAaτA,
(2-11)
联立式(2-4)、(2-8)、(2-10)、(2-11),解得
(2-12)
(2-13)
现在分析式(2-13),此式的值在θ∈[0, π/2)范围内为负,则α必大于π/2,也就是钝角.
由式(2-12)、(2-13)可求出杆对A球的作用F的大小和方向:
(2-14)
(2-15)
研究一下式(2-15),在θ∈[0, π/2)范围内α大于π/2,即杆对A球的作用力F的方向并不沿杆的方向,而是跟A球运动速度方向的夹角为钝角,瞬时功率P=Fv为负,说明杆必对A球做负功,这就验证了第(1)问中式(1-4)的结论.
用相同的办法,分析当杆转过的角度为θ时B的受力情况,并求出杆对B球的作用力F′的大小和方向:
F′sinα′-mBgcosθ=mBanB,
(2-16)
F′cosα′+mBgsinθ=mBaτB,
(2-17)
由以上两式及式(2-5)、(2-9)解得
(2-18)
(2-19)
分析式(2-19),不难看出,在θ∈[0, π/2)范围内,结果为正,α′必小于π/2,杆对B球的作用力F′的方向跟B球运动的速度方向的夹角为锐角,对B球做正功.
第三步,我们来讨论杆由水平位置转到竖直位置所需的时间.
由角速度的定义
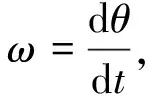
(3-1)
结合式(2-7),得
(3-2)
两边积分,即
(3-3)
得
(3-4)

故有
(3-5)
(3-6)
其中的Γ(x)是伽玛函数,是特殊函数之一.式(3-5)可写成:
(3-7)
至此,我们把案例中的三问全部求解完毕.
2.3 对案例求解过程的思考
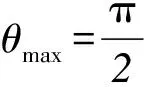
若将系统从偏离竖直方向一个很小的角度开始由静止释放,则可视为最大摆角趋于0,也就是复摆小角度振动,而复摆小角度振动周期可用理论力学中的结论求出.
由式(2-2),当θmax→0时,有
联立式(2-3),解得系统振动的角频率ω0满足
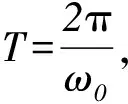
(4-1)
复摆小角度振动的四分之一周期
(4-2)
跟式(3-7)相比,有
(4-3)
可见,差别还是比较大的.案例中的系统从水平位置运动至竖直位置的过程不满足小角度振动的条件,因而所经历的时间不能简单地用复摆的周期来求解.
3 结语
通过对案例的求解可以看到,以轻杆约束的系统,往往是刚体,分析、求解除用到高中所学的知识外,还要综合运用刚体力学等物理规律,计算量大且复杂,大多要用到高等数学工具,超出了高中物理和数学的教学范围.但是,由轻杆构成的力学系统却是高中物理中非常普通的问题,在教学过程中是回避不了的,解决这类问题时,一不注意就会产生意想不到的错误,给教与学带来一些“麻烦”.怎样才能避免不必要的错误呢?笔者的建议是:
1)教师在命题时,将问题的设问尽可能地严格限制在高中物理和数学课程标准限定的范围内.
2)力学系统含有轻杆,在分析系统内部各部分之间的相互作用时要注意,不能轻易对杆的作用力的方向下结论.由于杆对与之连接的物体的弹力的方向可以沿任意方向, 所以不能先入为主地认为作用力沿杆的方向.在高中阶段,只考虑一种特殊情况,如果轻杆只有两点受力,那么杆对与之连接的物体的弹力的方向沿两个力的作用点的连线方向(就是通常所说的“杆的方向”).我们可以采用“试算法”:先按正常方法受力分析,然后按问题要求计算,再将计算结果“代入”问题中进行检验,从而得出原先的受力分析正确与否;如果不正确,再回过头来重新进行分析,原来的受力分析可能错在哪里,进行修正,再进行试算;如此不断反复“试算”,直到找到正确答案为止.以本文中的案例为例,我们可以先假定杆对两个小球的作用力沿杆的方向,这样,很容易得到杆对两球做的功为0;跟我们用功能原理求出的“做功不为0”的结论相矛盾,可见假设不成立;然后重做受力分析,假设杆对球的作用力不沿杆的方向(参照案例中的解法),再计算、验证,最终得出正确答案.
3)物理问题求解过程对数学水平要求较高,常常会用到一些复杂的数学知识,如微元法、微积分知识等,甚至会用到特殊函数论等数学理论及工具.建议找一些此类数学参考书放在手边,以便随时查阅.
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论

